Transformátor a magnetický indukční tok
Úloha číslo: 179
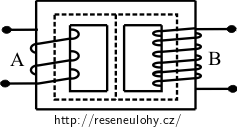
Na obrázku je znázorněno jádro transformátoru. Na jádru jsou navinuty cívky A a B. Magnetický indukční tok vznikající v kterékoli z těchto cívek nevystupuje z jádra, ale rozvětvuje se v něm tak, že jeho hodnoty v ostatních větvích jádra jsou navzájem stejné. Připojíme-li cívku A ke zdroji střídavého napětí 40 V s frekvencí 50 Hz, indukuje se na cívce B to samé napětí. Jaké napětí se bude indukovat na cívce A, připojíme-li naopak cívku B ke zdroji střídavého napětí 40 V s frekvencí 50 Hz?
Zápis
Ze zadání známe:
Napětí na zdroji střídavého napětí: U = 40 V Frekvenci střídavého napětí: f = 50 Hz Indukované napětí na cívkách: U1A = U1B = 40 V Indukované napětí na cívce B: U2B = 40 V Chceme určit:
Indukované napětí na cívce A: U2A = ? (V) Nápověda 1
Najděte si, jak spolu souvisí magnetický indukční tok, indukované napětí na cívce a počet závitů cívky.
Nápověda 2
Uvědomte si, že cívky A a B nemusí mít stejný počet závitů.
Rozbor
Magnetický indukční tok se v jádru transformátoru rozděluje takovým způsobem, že připojíme-li cívku A ke zdroji střídavého napětí, bude v cívce B a ve středu transformátoru poloviční magnetický indukční tok než uvnitř cívky A.
V následujícím odstavci si vyjádříme vztah mezi počty závitů cívek, který budeme pro konečný výpočet potřebovat. Víme, že připojíme-li ke zdroji střídavého napětí cívku A, pak známe napětí na obou cívkách ze zadání. Vyjdeme z Faradayova zákona pro indukované napětí na cívce a ze známého vztahu mezi magnetickými indukčními toky cívek. Vyjádříme tak vztah mezi počtem závitů obou cívek.
Připojíme-li nyní ke zdroji střídavého napětí cívku B, je vztah mezi magnetickým indukčním tokem cívky A a cívky B opačný než v případě popsaném výše. Navíc již známe poměr mezi počty závitů cívek. Pomocí těchto dvou vztahů vyjádříme napětí na cívce A.
Řešení
Pro velikost indukovaného napětí U na cívce podle Faradayova zákona platí
\[U=N\,\frac{ \Delta \Phi }{\Delta t}.\]Pro změnu magnetického indukčního toku ΦA cívky A platí
\[\frac{\Delta {\Phi}_\mathrm{A}}{\Delta t}=\frac{U_\mathrm{A}}{N_\mathrm{A}}.\]Pro změnu magnetického indukčního toku ΦB cívky B platí
\[\frac{\Delta {\Phi}_\mathrm{B}}{\Delta t}=\frac{U_\mathrm{B}}{N_\mathrm{B}}.\]1) Ke zdroji střídavého napětí 40 V je připojena cívka A.
Pro magnetický indukční tok cívek podle zadání platí Φ1A = 2 Φ1B. Dosadíme do vztahu pro cívku B:
\[\frac{\Delta {\Phi}_\mathrm{1B}}{\Delta t}=\frac{U_\mathrm{1B}}{N_\mathrm{B}}\ \Rightarrow \ \frac{\Delta {\Phi}_\mathrm{1A}}{\Delta t}=2 \frac{U_\mathrm{1B}}{N_\mathrm{B}}.\]Vyjádříme si také změnu magnetického indukčního toku cívky A:
\[\frac{\Delta {\Phi}_\mathrm{1A}}{\Delta t}=\frac{U_\mathrm{1A}}{N_\mathrm{1A}}.\]Porovnáme obě vyjádření pro změnu magnetického indukčního toku cívky A a dostaneme:
\[\frac{U_\mathrm{1A}}{N_\mathrm{1A}}=2 \frac{U_\mathrm{1B}}{N_\mathrm{1B}}.\]Ze zadání víme, že napětí U1A = U1B. Vyjádříme si vztah mezi počtem závitů obou cívek:
\[N_\mathrm{A}=\frac{1}{2}N_\mathrm{B}.\]2) Ke zdroji střídavého napětí 40 V je připojena cívka B.
Pro magnetické indukční toky mezi oběma cívkami nyní platí: Φ2B = 2 Φ2A. Dosadíme do vztahu pro vyjádření změny magnetického indukčního toku:
\[\frac{\Delta {\Phi}_\mathrm{2A}}{\Delta t}=\frac{1}{2}\frac{\Delta {\Phi}_\mathrm{2B}}{\Delta t}=\frac{U_\mathrm{2A}}{N_\mathrm{A}}\] \[\frac{\Delta {\Phi}_\mathrm{2B}}{\Delta t}=\frac{U_\mathrm{2B}}{N_\mathrm{B}}.\]Z druhé rovnice dosadíme do první rovnice za změnu magnetického indukčního toku a vyjádříme napětí na cívce A:
\[\frac{1}{2}\,\frac{U_\mathrm{2B}}{N_\mathrm{B}}=\frac{U_\mathrm{2A}}{N_\mathrm{A}}\] \[U_\mathrm{2A}=\frac{1}{2}N_\mathrm{A}\,\frac{U_\mathrm{2B}}{N_\mathrm{B}}.\]Dosadíme vztah mezi počtem závitů cívek: NA = 1/2 NB:
\[U_\mathrm{2A}=\frac{1}{2}\,\left(\frac{1}{2}N_\mathrm{B}\right)\,\frac{U_\mathrm{2B}}{N_\mathrm{B}}=\frac{1}{4}\,U_\mathrm{2B}.\]
Číselné dosazení:
\[U_\mathrm{2A}=\frac{1}{4}\cdot 40\,\mathrm V=10\,\mathrm V\]Odpověď
Připojíme-li cívku B ke zdroji střídavého napětí, bude se na cívce A, za podmínek popsaných v zadání, indukovat napětí 10 V.

