Pole rovnoměrně nabité sféry
Úloha číslo: 270
Na sféře o poloměru R je rovnoměrně rozmístěn náboj s plošnou hustotou σ.
a) Najděte intenzitu elektrického pole ve vzdálenosti z od středu sféry.
b) Určete také elektrický potenciál ve vzdálenosti z.
Uvažujte pole uvnitř i vně sféry, tzn. najděte průběh elektrické intenzity a potenciálu pro z v intervalu „od nuly až do nekonečna“.
Nápověda: Intenzita elektrického pole
Jako Gaussovu plochu zvolíme povrch koule o poloměru z se středem ve středu nabité sféry. V takovém případě je díky symetrii rozložení náboje vektor elektrické intenzity ve všech místech kolmý na plochu a má stejnou velikost. (Viz oddíl Jak volit Gaussovu plochu? v úloze Pole rovnoměrně nabité koule)
Úlohu rozdělíme na dva případy:- Poloměr Gaussovy koule je větší než poloměr nabité sféry.
- Poloměr Gaussovy koule je menší než poloměr nabité sféry.
Nápověda: Elektrický potenciál
Potenciální energie je rovna záporně vzaté práci, kterou musí vykonat elektrická síla, aby přenesla náboj z místa s nulovou potenciální energií (v našem případě z nekonečna) do daného místa:
\[E_\mathrm{p}(z)\,=\, - \int^\mathrm{z}_{\infty} \vec{F} \cdot \mathrm{d}\vec{z}.\]Potenciál je potenciální energie vztažená na jednotkový náboj:
\[\varphi\,=\, \frac{E_\mathrm{p}}{Q}.\]Dosadíme integrál:
\[\varphi\,=\, - \int^\mathrm{z}_{\infty} \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}.\]Jestliže sílu vydělíme nábojem, získáme intenzitu elektrického pole:
\[\varphi\,=\, - \int^\mathrm{z}_{\infty} \vec{E}\cdot \mathrm{d}\vec{z}.\]Nápověda: Potenciál uvnitř sféry
Pozor! Počítáme práci, kterou vykoná elektrická síla, když přenáší náboj z nekonečna. Do integrálu dosazujeme intenzitu elektrického pole, ta však nemá všude stejné vyjádření, ale musíme pro ni použít odlišné vzorce vně a uvnitř koule. Proto bude třeba integrál ve výrazu pro potenciál rozdělit na dvě části.Rozbor
Úlohu si rozdělíme na dvě části. Budeme zkoumat zvlášť pole uvnitř nabité sféry a zvlášť pole vně sféry.
Vzhledem k symetrickému rozložení náboje je nejjednodušším způsobem nalezení intenzity elektrického pole v tomto případě využití Gaussovy věty. Gaussova věta vyjadřuje vztah mezi tokem elektrické intenzity uzavřenou plochou a celkovým nábojem, který se nachází uvnitř této plochy.
Vektory elektrické intenzity míří ve všech místech od středu sféry směrem ven a jejich velikost závisí pouze na vzdálenosti od středu sféry. Důvodem je symetrické rozložení náboje na povrchu sféry. Může nám pomoci následující představa. Náboj je na povrchu rozložen symetricky, a proto nepoznáme žádný rozdíl, pokud sféru otočíme kolem libovolné osy jdoucí středem sféry. Pole kolem sféry musí zůstat stále stejné, a proto i vektory intenzity musím mít v daném místě při různých otočeních stále stejný směr a velikost.
Gaussovou plochou zvolíme povrch koule se středem ve středu nabité sféry. V tomto případě má vektor elektrické intenzity na celé této ploše stejnou velikost a je na ni kolmý. Tím se nám zjednoduší výpočet toku intenzity.
Počítáme-li intenzitu vně sféry, bude mít Gaussova koule větší poloměr než nabitá sféra. Uvnitř ní je tedy veškerý náboj rozložený na sféře, vyjádříme ho pomocí hustoty náboje a povrchu nabité sféry.
Počítáme-li intenzitu uvnitř nabité sféry, bude Gaussova koule mít menší poloměr než nabitá koule. Uvnitř plochy není uzavřený žádný náboj, a proto je zde intenzita rovna nule.
Potenciál elektrického pole vypočítáme z potenciální energie. Potenciální energie v daném bodě je rovna záporně vzaté práci, kterou vykonala elektrická síla, aby přenesla náboj z místa s nulovou potenciální energií do daného bodu. (Potenciální energii zvolíme nulovou v nekonečnu.) Potenciál je potenciální energie vztažená na jednotkový náboj.
Při výpočtu potenciálu uvnitř nabité sféry si musíme dát pozor na to, že intenzita elektrického pole nemá stejné vyjádření podél celé integrační cesty, ale je popsána jiným vztahem vně a uvnitř sféry. Musíme tedy spočítat nejprve práci, která je třeba k přenesení na povrch nabité sféry, a poté práci potřebnou k přesunu náboje uvnitř sféry.
Řešení: Intenzita vně sféry
V tomto oddíle vyjádříme intenzitu elektrického pole vně nabité sféry tzn. pro z>R.
Využijeme Gaussovu větu:
\[\oint_\mathrm{S} \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0}\,,\] \[\oint_\mathrm{S} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}.\tag{*}\]Protože je náboj na sféře rozložen symetricky, je také elektrické pole sféry symetrické. Vektor elektrické intenzity míří ve všech místech od středu sféry (tj. je kolmý na povrch sféry) a jeho velikost závisí pouze na vzdálenosti od středu sféry.
Jako Gaussovu plochu zvolíme povrch koule, která má poloměr z a střed ve středu nabité sféry (na obrázku naznačena zeleně). Plochu volíme takto proto, že vektor elektrické intenzity je kolmý k této Gaussově ploše a má stále stejnou velikost, což zjednoduší výpočet. (Jak volit Gaussovu plochu je popsáno v úloze Pole rovnoměrně nabité koule.)
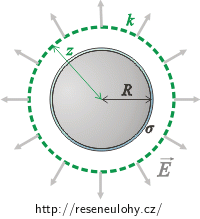
Vektor intenzity je ve všech místech rovnoběžný s normálovým vektorem a jejich skalární součin můžeme jednoduše spočítat:
\[\vec{E} \cdot \vec{n} \,=\, En \,=\, E\](pozn.: \(\vec{n}\) je jednotkový vektor).
S využitím těchto poznatků upravíme integrál na levé straně Gaussovy věty:
\[\oint_\mathrm{k} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_\mathrm{k} E n\mathrm{d}S\,=\, \oint_\mathrm{k} E\mathrm{d}S\,.\]Velikost vektoru elektrické intenzity E je ve všech místech zvolené plochy stejná, a proto ji můžeme vyjmout před integrál jako konstantu. Dostáváme tedy vztah
\[\oint_\mathrm{k} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_\mathrm{k} \mathrm{d}S.\]Nyní vypočítáme integrál. Integrujeme-li dS přes povrch koule, získáme obsah povrchu této koule. (Pozn.: Můžeme si to představit tak, že dS jsou obsahy malých kousků povrchu koule. Jestliže všechny tyto kousky sečteme, získáme celý povrch koule.) Integrál je tedy roven>
\[\oint_\mathrm{k} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E S_\mathrm{k},\]kde Sk = 4πz2 je povrch Gaussovy koule:
\[\oint_\mathrm{k} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E\, 4 \pi z^2.\]Výsledný vztah dosadíme zpět do Gaussovy věty (*):
\[E 4 \pi z^2\,=\, \frac{Q}{\varepsilon_0}.\]Vyjádříme velikost intenzity:
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{z^2}\tag{**}\]Vzorec je stejný jako pro intenzitu elektrického pole v okolí bodového náboje. Pole v okolí nabité sféry je tedy stejné jako pole v okolí bodového náboje umístěného ve středu sféry.
Zbývá už jen vyjádřit náboj Q uvnitř Gaussovy plochy pomocí zadaných veličin.
Uvnitř plochy je celá nabitá sféra, náboj tedy můžeme vyjádřit pomocí jejího povrchu S a plošné hustoty náboje σ:
\[Q\,=\,S \sigma\,=\,4 \pi R^2 \sigma.\]Dosadíme do vzorce (**) a upravíme:
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{4 \pi R^2 \sigma}{z^2}\,=\, \frac{\sigma R^2}{\varepsilon_0\,z^2}.\]Ve vzdálenosti z má intenzita elektrického pole nabité sféry velikost:
\[E \,=\, \frac{\sigma R^2}{\varepsilon_0\,}\,\frac{1}{z^2}\,.\]Řešení: Intenzita uvnitř sféry
Intenzitu elektrického pole uvnitř nabité sféry určíme opět pomocí Gaussovy věty:
\[\oint_\mathrm{S} E \cdot \mathrm{d}S \,=\, \frac{Q}{\epsilon_0}\,,\]kde Q je náboj uzavřený uvnitř Gaussovy plochy.
Jako Gaussovu plochu zvolíme opět povrch koule se středem ve středu nabité sféry a o poloměru z. Tok intenzity touto plochou (tj. levou stranu Gaussovy věty) spočítáme úplně stejně jako v předchozím případě.
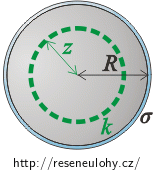
Protože zvolená plocha je uvnitř nabité sféry, není v ní uzavřen žádný náboj, tj. Q = 0.
Intenzita elektrického pole uvnitř sféry je tedy rovna nule.
Řešení: Potenciál vně sféry
Potenciál v bodě A se až na znaménko rovná integrálu intenzity z místa s nulovým potenciálem do bodu A. Nulový potenciál zvolíme v nekonečnu (podrobnější vysvětlení je uvedeno v nápovědě):
\[\varphi (z)\,=\, - \int_{\infty}^\mathrm{z} \vec{E} \cdot \mathrm{d}\vec{z}.\]Protože intenzita elektrického pole závisí pouze na vzdálenosti od středu koule, závisí i potenciál elektrického pole pouze na vzdálenosti z od středu koule.
Potenciál nezávisí na volbě integrační cesty, proto ji můžeme volit libovolně. (Cestu si volíme co nejjednodušší.) V tomto případě jako integrační cestu zvolíme část přímky, která směřuje do středu koule.
Vektor elektrické intenzity \(\vec{E}\) je rovnoběžný s vektorem \(\vec{z}\), proto můžeme integrál zjednodušit:
\[ \varphi (z)\,=\, - \int^\mathrm{z}_{\infty} E \mathrm{d}z. \]Nyní musíme úlohu opět rozdělit na dva případy a spočítat zvlášť potenciál vně a uvnitř sféry.
Nejprve vyjádříme potenciál ve vzdálenosti z vně sféry:
\[\varphi (z)\,=\, - \int^\mathrm{z}_{\infty} E \mathrm{d}z. \]Do integrálu dosadíme velikost intenzity, kterou jsme si vyjádřili v oddíle Intenzita pole vně sféry:
\[E \,=\, \frac{\sigma R^2}{\varepsilon_0}\,\frac{1}{z^2}\,\]a vytkneme před integrál všechny konstanty:
\[\varphi (z)\,=\, - \int^\mathrm{z}_{\infty} \frac{\sigma R^2}{\varepsilon_0}\,\frac{1}{z^2} \,\mathrm{d}z \,=\, - \,\frac{\sigma R^2}{\varepsilon_0} \int^\mathrm{z}_{\infty} \frac{1}{z^2}\, \mathrm{d}z.\]Vypočítáme určitý integrál:
\[\varphi (z)\,=\,- \,\frac{\sigma R^2}{\varepsilon_0}\left[- \frac{1}{z}\right]^\mathrm{z}_{\infty}\,.\]Dosadíme meze integrálu a získáme velikost potenciálu vně sféry ve vzdálenosti z:
\[\varphi (z)\,=\,\frac{\sigma R^2}{\varepsilon_0}\frac{1}{z}.\tag{+}\]Pozn.: Pokud chceme potenciál vyjádřit pomocí celkového náboje Q, využijeme vztahu \(Q\,=\,4 \pi R^2 \sigma\).
Pro potenciál vně koule pak platí vztah:
\[\varphi (z)\,=\, \frac{Q}{4 \pi \epsilon_0} \, \frac{1}{z}\,.\]Řešení: Potenciál uvnitř sféry
Uvnitř sféry je intenzita elektrického pole ve všech místech stejná a je rovna nule. Proto i potenciál bude uvnitř sféry všude stejný, ale není nulový. Vypočítáme ho podobně jako v předchozím oddíle.
Potenciál vyjádříme ze vztahu:
\[\varphi (z)\,=\, - \int^\mathrm{z}_{\infty} \vec{E} \cdot \mathrm{d}\vec{z}\,=\, - \int^\mathrm{z}_{\infty} E \mathrm{d}z\,.\]Při vyjadřování potenciálu si musíme dát pozor na velikost intenzity. Tentokrát není intenzita elektrického pole vyjádřena podél celé integrační cesty stejným vztahem. Hranicí, kdy se vyjádření intenzity mění, je povrch sféry. Proto je třeba celý integrál rozdělit na dvě části. Nejdříve musíme náboj přenést z nekonečna na povrch (tj. do vzdálenosti R od středu sféry) a poté z povrchu sféry dále dovnitř sféry:
\[\varphi (z)\,=\, - \int^\mathrm{R}_{\infty} E_\mathrm{v} \mathrm{d}z \,- \int^\mathrm{z}_\mathrm{R}E_\mathrm{u} \mathrm{d}z.\]Protože uvnitř sféry je intenzita vždy rovna nule, je také druhý integrál roven nule.
První integrál jsme již počítali v předchozím oddíle (viz vzorec (+)):
\[\varphi (z)\,=\, - \int^\mathrm{z}_{\infty} E_\mathrm{v} \mathrm{d}z \,=\,\frac{\sigma R^2}{\varepsilon_0} \frac{1}{z}.\]Integrál se ale lišil horní mezí. Do výsledku předchozího oddílu musíme tedy dosadit z = R:
\[\varphi (z)\,=\, \,\frac{\sigma R^2}{\varepsilon_0}\, \frac{1}{R}.\]Po zkrácení získáme velikost potenciálu uvnitř sféry:
\[\varphi (z)\,=\, \,\frac{\sigma R}{\varepsilon_0}.\]Uvnitř sféry je tedy stejný potenciál jako na jejím povrchu.
Pozn.: Pokud bychom chtěli vyjádřit potenciál pomocí celkového náboje Q, využijeme opět vztahu \(Q\,=\,4 \pi R^2 \sigma\) a dostaneme
\[\varphi (z)\,=\, \,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{R}\,.\]Odpověď
Vně sféry míří vektor intenzity elektrického pole ze středu sféry směrem ven a má velikost
\[E \,=\, \frac{1}{4 \pi \varepsilon_0}\,\frac{Q}{z^2}\,=\,\frac{\sigma R^2}{\varepsilon_0\,}\,\frac{1}{z^2}\,.\]Uvnitř sféry je intenzita elektrického pole nulová.
Elektrický potenciál vně nabité sféry má velikost
\[\varphi (z)\,=\,\frac{\sigma R^2}{\varepsilon_0}\frac{1}{z}\,=\, \frac{Q}{4 \pi \epsilon_0} \, \frac{1}{z}\,.\]Elektrický potenciál uvnitř nabité sféry je konstantní a je roven
\[\varphi (z)\,=\,\frac{\sigma R}{\varepsilon_0}\,=\, \frac{Q}{4 \pi \epsilon_0} \, \frac{1}{R}\,.\]Grafy
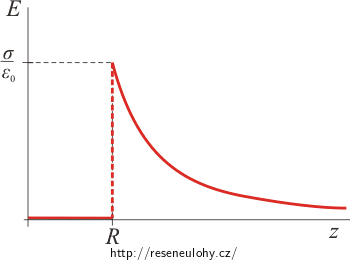
Graf závislosti velikosti el. intenzity na vzdálenosti od středu koule
Uvnitř nabité sféry je elektrická intenzita rovna nule.
Vně koule platí vztah \(E \,=\, \frac{\sigma R^2}{ \varepsilon_0}\, \frac{1}{z^2} \,.\)
Graf funkce není spojitý. První část grafu (pro hodnoty z od 0 do R) tvoří konstantní funkce, která prochází počátkem. Ve vzdálenosti z = R se intenzita mění skokem na hodnotu \(E(R)\,=\,\frac{ \sigma}{ \varepsilon_0}\,.\) Pro vzdálenost z větší než R pak intenzita s druhou mocninou z klesá.
Pozn.: Intenzita elektrického pole je spojitá s výjimkou bodů, kdy prochází nabitou plochou. Při průchodu plochou zůstávají spojité pouze tečné složky vektoru. Normálové složky se mění „skokem“, který je úměrný plošné hustotě náboje, což v našem případě platí.
Graf závislosti el. potenciálu na vzdálenosti od středu koule
Elektrický potenciál uvnitř nabité sféry je konstantní a roven \(\varphi (z)\,=\, \,\frac{\sigma R}{ \varepsilon_0}\,.\)
Vně nabité sféry platí vztah \(\varphi (z)\,=\, \,\frac{\sigma R^2}{\varepsilon_0}\frac{1}{z}\,.\)
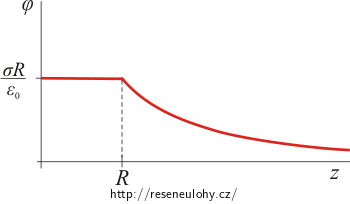
Funkce je v bodě z = R spojitá. Dosadíme-li do obou vyjádření potenciálu, získáme v obou případech hodnotu \(\varphi(R) \,=\,\frac{\sigma R }{ \varepsilon_0}\).
V tomto bodě nemá funkce spojité první derivace, proto funkce není v tomto bodě hladká.
Pozn.: Elektrický potenciál je vždy spojitý, protože se jedná vlastně o práci při přenášení jednotkového náboje a ta se nemůže změnit „skokově“. Kromě nabitých ploch má potenciál spojité také první derivace, tj. je hladký.



