Sbírka řešených úloh

Kulička ztratí náboj

Úloha číslo: 717

• Nápověda 1

  Jaké síly působí na nabité kuličky?

  Která ze sil přestane působit, jestliže jedna kulička ztratí náboj?

• Nápověda 2

  Jestliže jedna kulička ztratí náboj, přestane působit elektrostatická síla a kuličky se srazí. Co se stane s nábojem při dotyku kuliček?

• Řešení nápovědy

  Protože jsou kuličky vodivé, náboj se po nich může volně pohybovat, a tedy se náboj z druhé kuličky při dotyku rovnoměrně rozdělí na obě kuličky. Díky tomu elektrostatická síla opět začne působit.

  Do jaké vzdálenosti se kuličky oddálí nyní, když je náboj menší?

• Rozbor

  Protože jsou kuličky nabité stejným nábojem, působí na ně kromě tíhové síly také elektrostatická odpudivá síla. Velikost této síly je dána Coulombovým zákonem.

  Po ztrátě náboje přestane mezi kuličkami působit elektrostatická odpudivá síla, což způsobí, že se kuličky srazí. Kuličky jsou vodivé, a tak se na nich při této srážce vyrovná náboj. Protože platí zákon zachování náboje, náboj Q z nabité kuličky se rovnoměrně rozdělí na obě kuličky. Každá kulička bude tedy nabita nábojem \(\frac{Q}{2}\).

  Opět mezi nimi tedy začne působit elektrostatická odpudivá síla, jenž způsobí oddálení kuliček. Vzhledem ke zmenšení náboje se však kuličky oddálí do menší vzdálenosti, než v jaké se nacházely na počátku.

  

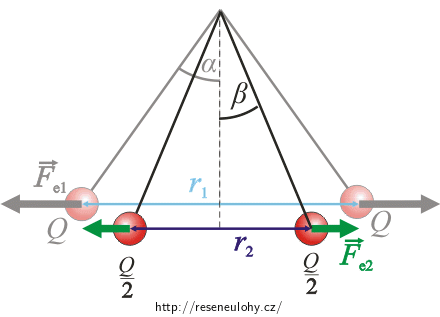
  K výpočtu vzdálenosti využijeme goniometrických funkcí a podobnosti trojúhelníků.

  

  Z červeného trojúhelníku vyjádříme pomocí funkce tangens vztah mezi úhlem alpha a oběma silami. Protože pro malé úhly je funkce tangens stejná jako funkce sinus, vyjádříme v modrém trojúhelníku funkci sinus a oba vztahy porovnáme.

  Stejný postup provedeme i pro situaci po srážce. Porovnáním získaných vzorců získáme vztah pro výpočet vzdálenosti.

• Řešení

  

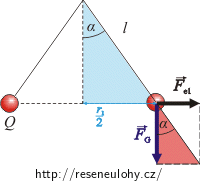
  Před ztrátou náboje platí z červeného trojúhelníka vztah:

  \[\mathrm{tg}\alpha\,=\,\frac{F_\mathrm{e1}}{F_G}\,.\]

  Dosadíme vyjádření elektrické síly z Coulombova zákona a tíhové síly:

  \[\mathrm{tg}\alpha\,=\,\frac{\frac{1}{4\pi\varepsilon_0}\frac{Q^2}{r_1^2}}{mg}\,=\,\frac{Q^2}{4\pi\varepsilon_0mgr_1^2}.\]

  

  Po ztrátě náboje se obě kuličky dotknou a náboj Q se rovnoměrně rozdělí na obě kuličky. Každá bude tedy nabita nábojem \(\frac{Q}{2}\). Vlákno bude nyní svírat se svislým směrem úhel β.

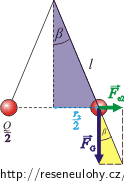
  Ze žlutého trojúhelníka bude platit vztah:

  \[\mathrm{tg}\beta\,=\,\frac{F_\mathrm{e2}}{F_\mathrm{G}}\,=\,\frac{\left(\frac{Q}{2}\right)^2}{4\pi\varepsilon_0mgr_2^2}\,=\,\frac{Q^2}{16\pi\varepsilon_0mgr_2^2}\,,\]

  kde r₂ je nová vzdálenost kuliček.

   

  Protože jsou kuličky zavěšeny na velmi dlouhých vláknech, jsou úhly α a β velmi malé. Pro malé úhly platí přibližný vztah sinα ≈ tgα (viz poslední oddíl úlohy). Z tohoto důvodu můžeme s využitím modrého trojúhelníku psát:

  \[\mathrm{tg}\alpha\,\dot=\,\sin\alpha=\,\frac{r_1}{2l}\] \[\frac{Q^2}{4\pi\varepsilon_0mgr_1^2}\,\dot=\,\frac{r_1}{2l}\hspace{40px}|\cdot r_1^2\] \[\frac{Q^2}{4\pi\varepsilon_0mg}\,\dot=\,\frac{r_1^3}{2l}\tag{1}\]

  Stejný postup uplatníme i pro úhel β:

  \[\mathrm{tg}\beta\,\dot=\,\sin\beta,\] \[\frac{Q^2}{16\pi\varepsilon_0mgr_2^2}\,\dot=\,\frac{r_2}{2l}\hspace{40px}|\cdot 4 r_2^2,\] \[\frac{Q^2}{4\pi\varepsilon_0mg}\,\dot=\,\frac{4 r_2^3}{2l}.\tag{2}\]

  Porovnáním vztahů (1) a (2) získáváme:

  \[\frac{r_1^3}{2l}\dot=\,\frac{4 r_2^3}{2l}\,.\] Nyní už vyjádříme vzdálenost r₂ kuliček po dotyku: \[r_1^3\dot=\,4 r_2^3,\] \[\frac{r_1^3}{4}\dot=\, r_2^3,\] \[r_2\,\dot=\,\frac{r_1}{\sqrt[3]{4}}.\]

• Zápis a číselný výpočet

  r1 = 4 cm	počáteční vzdálenost kuliček
  r2 = ? cm	vzdálenost kuliček po dotyku

  ---

  \[r_2\,\dot=\,\frac{r_1}{\sqrt[3]{4}}\,\dot=\,\frac{4}{\sqrt[3]{4}}\,\dot=\,2{,}5\,\mathrm{cm}\]

  Pozn.: V této úloze není třeba převádět jednotky, jelikož výsledek získáváme pouze vydělením číslem. Jednotka výsledku tedy zůstává stejná jako jednotka u dosazené veličiny.

• Odpověď

  Kuličky se po vzájemném dotyku způsobeném ztrátou náboje jedné z nich oddálí do vzdálenosti \(r_2\,\dot=\,\frac{r_1}{\sqrt[3]{4}}\,\dot=\,2{,}5\,\mathrm{cm}.\)

• Funkce sinus a tangens pro malé úhly

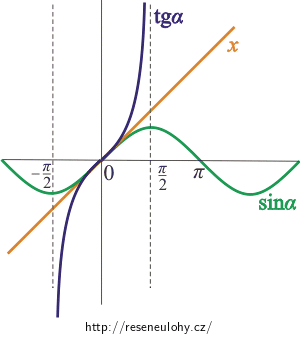
  Pro malé úhly jsou hodnoty funkce sinus téměř shodné s hodnotami funkce tangens: sinα ≈ tgα.

  Lze to dobře vidět, když zakreslíme průběhy obou funkcí do jednoho grafu. Pro malé úhly (oblast označená červeně) se obě funkce překrývají.

  

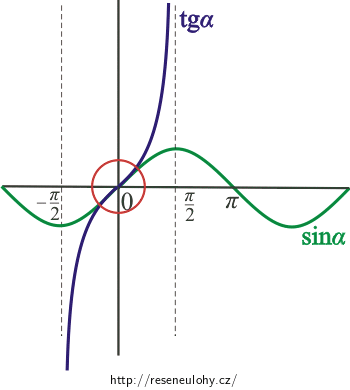
  Pro tuto oblast malých úhlů dokonce platí, že průběh funkce sinus a tangens je stejný s průběhem funkce f_(x) = x. Je třeba dávat pozor na jednotky, protože tato vlastnost platí pouze tehdy, když velikost úhlu dosazujeme v radiánech!