Kondenzátory
Úloha číslo: 24
Na obrázku je schéma zapojení tří kondenzátorů C1, C2 a C3. Na baterce je napětí U.
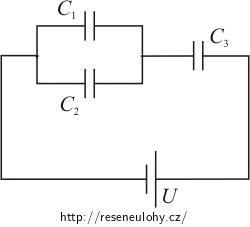
a) Určete celkovou kapacitu zapojení a celkový náboj Q na kondenzátorech.
b) Určete náboj a napětí na každém z kondenzátorů.
Nápověda: Kapacita
Při paralelním zapojení kondenzátorů je celková kapacita rovna součtu jednotlivých kapacit:
\[C\,=\,C_1+C_2+C_3.\]Při sériovém zapojení je převrácená hodnota celkové kapacity rovna součtu převrácených hodnot jednotlivých kapacit:
\[\frac{1}{C}\,=\,\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}.\]Nápověda: Napětí a náboj
Při sériovém zapojení kondenzátorů je na všech kondenzátorech stejný náboj. Napětí se v tomto případě sčítají:
\[Q\,=\,Q_1\,=\,Q_2\,=\,Q_3,\] \[U\,=\,U_1+U_2+U_3.\]Při paralelním zapojení se náboje na jednotlivých kondenzátorech sčítají. Napětí je na všech kondenzátorech stejné:
\[Q\,=\,Q_1+Q_2+Q_3,\] \[U\,=\,U_1\,=\,U_2\,=\,U_3.\]Rozbor
Paralelně zapojené kondenzátory můžeme nahradit jedním kondenzátorem s kapacitou, která je rovna součtu kapacit na obou kondenzátorech. Tím získáme obvod jen se dvěma sériově zapojenými kondenzátory. Při sériovém zapojení je převrácená hodnota celkové kapacity rovna součtu převrácených hodnot kapacit jednotlivých kondenzátorů. Tak určíme celkovou kapacitu.
Celkový náboj je přímo úměrný celkové kapacitě a celkovému napětí (tj. napětí na baterii).
Náboje na sériově zapojených kondenzátorech jsou stejné a v našem případě jsou rovny celkovému náboji. Náboj na třetím kondenzátoru je proto roven celkovému náboji. Pomocí známé kapacity dopočítáme napětí na třetím kondenzátoru.
Napětí na obou paralelně zapojených kondezátorech je stejné. Můžeme ho určit jako rozdíl celkového napětí a napětí na třetím kondenzátoru. Pomocí kapacity dopočítáme náboj na těchto kondenzátorech.
Řešení: Celková kapacita a celkový náboj
Paralelně zapojené kondenzátory C1 a C2 můžeme nahradit jedním kondenzátorem C12 s kapacitou rovnou součtu jednotlivých kapacit: C12 = C1+C2.
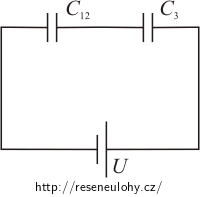
V obvodu máme nyní dva kondenzátory C12 a C3 zapojeny sériově.
Pro ně platí:
\[\frac{1}{C}\,=\,\frac{1}{C_{12}}+\frac{1}{C_3}\, \Rightarrow\,C\,=\,\frac{C_{12}C_3}{C_{12}+C_3}.\]Do vzorce dosadíme za kapacitu C12 a máme vyjádřenou neznámou celkovou kapacitu C:
\[C\,=\,\frac{(C_1+C_2)C_3}{C_1+C_2+C_3}.\]Celkový náboj vypočítáme ze vztahu Q = UC.
Dosadíme za celkovou kapacitu C a dostaneme celkový náboj Q:
\[Q\,=\,\frac{U(C_1+C_2)C_3}{C_1+C_2+C_3}.\tag{1}\]Řešení: Náboje a napětí na jednotlivých kondenzátorech
Náboj a napětí na třetím kondenzátoru:
Náboj na kondenzátorech C12 a C3 je stejný a je roven celkovému náboji Q:
\[Q\,=\,Q_{12}\,=\,Q_3.\]Napětí na třetím kondenzátoru je tedy:
\[U_3\,=\,\frac{Q_3}{C_3}\,=\,\frac{Q}{C_3}.\]Za náboj Q dosadíme ze vztahu (1), který jsme si spočetli v předchozí části Celková kapacita a celkový náboj:
\[U_3\,=\,\frac{U \left( C_1+C_2 \right)C_3}{ \left( C_1+C_2+C_3\right)C_3}\,= \,\frac{U \left( C_1+C_2 \right)}{ C_1+C_2+C_3}.\tag{*}\]
Napětí na paralelně zapojených kondenzátorech:
Celkové napětí U se rozdělí na kondenzátory C12 a C3:
\[U\,=\,U_{12}+U_3.\]Z tohoto vztahu můžeme spočítat napětí U12:
\[U_{12}\,=\,U-U_3.\]Dosadíme za napětí U3 ze vzorce (*):
\[U_{12}\,=\,U-\frac{U \left( C_1+C_2 \right)}{ C_1+C_2+C_3}.\]Převedeme na společného jmenovatele a zjistíme, že některé členy se nám odečtou:
\[U_{12}\,=\,\frac{U \left( C_1+C_2+C_3 \right)-U \left( C_1+C_2 \right)}{ C_1+C_2+C_3}\,=\,\frac{UC_3}{ C_1+C_2+C_3}.\tag{**}\]Napětí na paralelně zapojených kondenzátorech C1 a C2 je stejné:
\[U_1\,=\,U_2\,=\,U_{12}.\]
Náboj na paralelně zapojených kondenzátorech:
Nyní můžeme pomocí kapacit a napětí spočítat náboj na prvním a druhém kondenzátoru:
\[Q_1=U_1C_1,\] \[Q_2=U_2C_2.\]Za napětí dosadíme ze vzorce (**) a máme vyjádřený náboj Q1 a Q2:
\[Q_1=\,\frac{UC_1C_3}{ C_1+C_2+C_3},\] \[Q_2=\,\frac{UC_2C_3}{ C_1+C_2+C_3}.\]Výsledné vzorce
Celková kapacita obvodu a celkový náboj:
\[C\,=\,\frac{(C_1+C_2)C_3}{C_1+C_2+C_3}\] \[Q\,=\,\frac{U(C_1+C_2)C_3}{C_1+C_2+C_3}\]Náboje na jednotlivých kondenzátorech:
\[Q_1\,=\,\frac{UC_1C_3}{C_1+C_2+C_3}\] \[Q_2\,=\,\frac{UC_2C_3}{C_1+C_2+C_3}\] \[Q_3\,=\,Q\]Napětí na jednotlivých kondenzátorech:
\[U_1\,=\,U_2\,=\,\frac{UC_3}{C_1+C_2+C_3}\] \[U_3\,=\,\frac{U\left(C_1+C_2\right)}{C_1+C_2+C_3}\]




