Jakou silou napíná nabitá kulička nit
Úloha číslo: 736
V homogenním elektrickém poli o intenzitě 106 V m−1 visí na niti kulička o hmotnosti 2 g nabitá nábojem 10 nC. Vektor intenzity svírá se svislicí úhel 30°.
Určete, jak velkou silou je napínána nit.
Nápověda
Nakreslete si obrázek sil působících na kuličku. Co pro tyto síly platí, jestliže je kulička v klidu?
K výpočtu tahové síly využijte kosinové věty.
Nápověda: Rozdělení úlohy
Uvědomte si, že jsou dvě možnosti orientace vektoru intenzity. Úlohu vypočítejte pro každý případ zvlášť.
Rozbor
Na kuličku zavěšenou na vlákně v elektrickém poli působí tíhová síla, tahová síla vlákna a elektrická síla. Protože je kulička v klidu, musí být výslednice těchto sil rovna nule.
Směr elektrické síly je stejný jako směr vektoru intenzity elektrického pole. Ten může být orientován dvěma způsoby (viz obrázek).
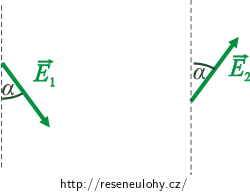
Úlohu tedy rozdělíme na dva případy. V obou případech vypočítáme velikost tahové síly z kosinové věty.
Řešení: Obrázek situace a rozdělení úlohy
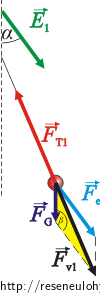
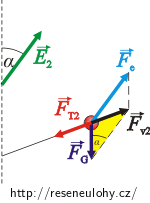
Intenzita může být orientována dvěma způsoby (viz obrázek). V obou případech na kuličku působí tíhová síla \(\vec{F}_\mathrm{G}\), elektrická síla \(\vec{F}_\mathrm{e}\) a tahová síla niti \(\vec{F}_\mathrm{T}\), jejíž velikost hledáme.
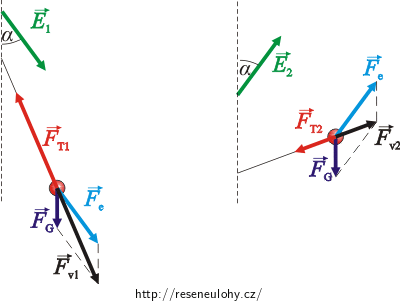
Celou úlohu tedy rozdělíme na dva případy.
Řešení: První případ
Na kuličku působí tíhová síla \(\vec{F}_\mathrm{G}\), elektrická síla \(\vec{F}_\mathrm{e}\) a tahová síla niti \(\vec{F}_\mathrm{T}\), jejíž velikost hledáme.
V rovnováze musí platit, že výsledná síla působící na kuličku je nulová. To znamená, že tahová síla niti musí mít stejnou velikost a opačný směr vůči výslednici tíhové a elektrické síly.
Velikost této výslednice určíme pomocí kosinové věty ze žlutého trojúhelníku (znění kosinové věty naleznete v první nápovědě):
\[F_\mathrm{v1}^2\,=\,F_\mathrm{G}^2\,+\,F_\mathrm{e}^2\,-\,2 F_\mathrm{G} F_\mathrm{e} \cos \beta. \tag{1}\]Velikost tíhové a elektrické síly získáme pomocí následujících vztahů:
\[F_\mathrm{G}\,=\,mg\,, \hspace{30px} F_\mathrm{e}\,=\,QE.\]Pro úhly α a β platí: α + β = 180° (viz obrázek po zvětšení). Velikost úhlu β vypočítáme tedy jako: β = 180° − α.
Vyjádření všech veličin dosadíme do vzorce (1):
\[F_\mathrm{v1}^2\,=\,m^2 g^2\,+\,Q^2 E^2\,-\,2 mgQE \cos\left(180^\circ - \alpha\right). \]Pro funkci kosinus platí cos(180° − α) = −cosα. Můžeme tak vzorec zjednodušit na
\[F_\mathrm{v1}^2\,=\,m^2 g^2\,+\,Q^2 E^2\,+\,2 mgQE \cos\alpha .\]Nyní už jen vyjádříme velikost výsledné síly (a tedy i síly tahové):
\[F_\mathrm{T1}\,=\,F_\mathrm{v1}\,=\,\sqrt{m^2 g^2\,+\,Q^2 E^2\,+\,2 mgQE \cos \alpha }\,.\]Řešení: Druhý případ
Postup řešení je velmi podobný, liší se pouze velikostí dosazeného úhlu.
Velikost výslednice tíhové a elektrické síly získáme opět pomocí kosinové věty ze žlutého trojúhelníku:
\[F_\mathrm{v2}^2\,=\,F_\mathrm{G}^2\,+\,F_\mathrm{e}^2\,-\,2 F_\mathrm{G} F_\mathrm{e} \cos \alpha. \]Stejně jako v předchozím případě dosadíme velikost tíhové a elektrické síly z následujících vzorců FG = mg, Fe = QE:
\[F_\mathrm{v2}^2\,=\,m^2 g^2\,+\,Q^2 E^2\,-\,2 mgQE \cos\alpha .\]Nyní už jen vyjádříme velikost výsledné síly (a tedy i síly tahové):
\[F_\mathrm{T2}\,=\,F_\mathrm{v2}\,=\,\sqrt{m^2 g^2\,+\,Q^2 E^2\,-\,2 mgQE \cos\alpha}.\]Zápis a číselný výpočet
E = 106 V m−1 velikost intenzity elektrického pole m = 2 g = 2·10−3 hmotnost kuličky α = 30° úhel, který svírá vektor intenzity se svislicí Q = 10 nC = 1·10−8 C náboj kuličky Z tabulek g = 9,81 m s−2 tíhové zrychlení
\[F_\mathrm{T1}\,=\,\sqrt{m^2 g^2\,+\,Q^2 E^2\,+\,2 mgQE \cos\alpha} \] \[F_\mathrm{T1} =\sqrt{4{\cdot} 10^{-6} \cdot 9{,}81^2\,+\,10^{-16} \cdot10^{12}+2 {\cdot} 2\cdot 10^{-3} \cdot 9{,}81{\cdot} 10^{-8}\cdot10^6 \cdot \cos 30^\circ}\] \[F_\mathrm{T1}\,\dot=\,2{,}87{\cdot}10^{-2}\,\mathrm{N}\,\dot=\,29\,\mathrm{mN}\]
\[F_\mathrm{T2}\,=\,\sqrt{m^2 g^2\,+\,Q^2 E^2\,-\,2 mgQE \cos\alpha} \] \[F_\mathrm{T2} =\sqrt{4{\cdot} 10^{-6} \cdot 9{,}81^2\,+\,10^{-16} \cdot10^{12}-2 {\cdot} 2\cdot 10^{-3} \cdot 9{,}81{\cdot} 10^{-8}\cdot10^6 \cdot \cos 30^\circ}\] \[F_\mathrm{T1}\,\dot=\,1{,}2{\cdot}10^{-2}\,\mathrm{N}\,\dot=\,12\,\mathrm{mN}\]Odpověď
V prvním případě bude nit napínána silou
\[F_\mathrm{T1}\,=\,\sqrt{m^2 g^2\,+\,Q^2 E^2\,+\,2 mgQE \cos\alpha}\,\dot=\,29\,\mathrm{mN}\,,\]ve druhém silou
\[F_\mathrm{T2}\,=\,\sqrt{m^2 g^2\,+\,Q^2 E^2\,-\,2 mgQE \cos\alpha}\,\dot=\,12\,\mathrm{mN}\,.\]