Vzájemné silové působení dvou vodičů s proudem

Úloha číslo: 479

Dvěma rovnoběžnými vodiči ve vzájemné vzdálenosti 10 cm procházejí proudy 10 A a 20 A. Určete velikost a směr magnetické síly, která působí na 1 m délky vodičů, jestliže oba proudy mají a) stejný směr, b) opačný směr.

Nápověda
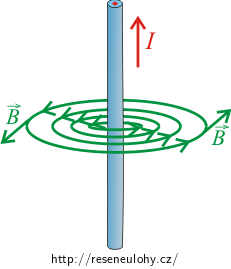
Nakreslete si magnetická pole, která ve svém okolí vytváří přímé vodiče s proudem.

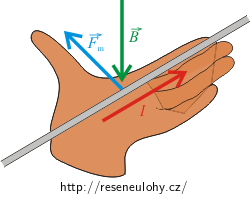
Protože se jeden z vodičů nachází v magnetickém poli druhého vodiče, bude na něj působit magnetická síla, jejíž velikost bude úměrná velikosti magnetického pole od druhého vodiče, proudu prvním vodičem a délce vodiče. Směr této síly určíte pomocí Flemingova pravidla levé ruky.
Řešení nápovědy – Magnetické pole přímého vodiče s proudem
V okolí vodiče, kterým prochází elektrický proud, se vytváří magnetické pole charakterizované magnetickou indukcí. Indukční čáry vektoru magnetické indukce \(\vec{B}\) mají tvar soustředných kružnic se středem ve vodiči.

Směr vektoru magnetické indukce \(\vec{B}\) určíme pomocí Ampérova pravidla pravé ruky a to tak, že položíme palec pravé ruky ve směru proudu ve vodiči a zahnuté prsty ukazují směr magnetických indukčních čar.

Pro velikost vektoru magnetické indukce B od dlouhého přímého vodiče s proudem platí vztah
\[B= \frac{\mu_\mathrm{0}}{2\pi}\,\frac{I}{R},\]
kde I je proud procházející vodičem a R je kolmá vzdálenost od vodiče, ve které určujeme velikost magnetické indukce.

Vztah je zde uveden bez odvození, protože jej nelze odvodit prostředky středoškolské matematiky. Podrobné odvození pomocí vysokoškolské matematiky naleznete v úloze Magnetické pole dlouhého přímého vodiče s proudem.
Řešení nápovědy – Velikost a směr magnetické síly
Na vodič s proudem, který se nachází v magnetickém poli, působí magnetická síla \(\vec{F}_\mathrm{m}\), pro jejíž velikost platí
\[F_\mathrm{m}=BIl\,\sin{\alpha},\]
kde B je velikost magnetické indukce magnetického pole, ve kterém se vodič nachází, a úhel α je úhel mezi vektorem magnetické indukce a směrem proudu ve vodiči.

Každý z vodičů leží v magnetickém poli, které vytváří druhý vodič. Pokud jsou vodiče rovnoběžné, potom vektor magnetické indukce tohoto magnetického pole je kolmý na směr proudu procházející příslušným vodičem (viz obrázek), tedy
\[\alpha=90^\circ\,\,\,\Rightarrow\,\,\sin{\alpha} =1.\]

Pro velikost magnetické síly, která bude působit na vodič s proudem, dostáváme výraz
\[F_\mathrm{m}=BIl,\]
kam za B dosadíme magnetickou indukci pole, které vytváří např. první vodič v místě druhého vodiče, a za I proud, který teče druhým vodičem, nebo naopak.

Směry sil určíme pomocí Flemingova pravidla levé ruky.

Flemingovo pravidlo levé ruky

Položíme-li k vodiči levou ruku tak, aby natažené prsty ukazovaly směr proudu a magnetické indukční čáry (respektive vektor \(\vec{B}\)) vstupovaly do dlaně, ukazuje odtažený palec směr a orientaci vektoru magnetické síly \(\vec{F}_\mathrm{m}\), která působí na vodič.
Rozbor
V okolí obou vodičů, kterými prochází elektrické proudy, se vytváří magnetická pole charakterizovaná magnetickou indukcí. Tato pole si nakreslíme a směry vektorů magnetické indukce určíme pomocí Ampérova pravidla pravé ruky.

Každý z vodičů se nachází v magnetickém poli vytvořeném druhým vodičem. Protože vodiči prochází elektrické proudy a nacházejí se v magnetickém poli, působí na ně magnetické síly. Velikost magnetických sil závisí na velikosti magnetického pole, ve kterém se vodič nachází, na proudu procházejícím vodičem, délce vodiče a na poloze vodiče vůči vektoru magnetické indukce. Protože vodiče, jimiž prochází elektrické proudy a v jejichž okolí se vytváří magnetická pole, jsou rovnoběžné, vektor magnetické indukce je vždy kolmý na směr proudu ve vodiči (viz vysvětlení v oddíle Nápověda).

Magnetické pole, ve kterém se jeden z vodičů nachází, je magnetické pole vytvořené druhým vodičem. Do vztahu pro velikost magnetické síly dosadíme velikost magnetické indukce od dlouhého přímého vodiče (v tomto případ toho druhého), kde se vzdálenost, ve které magnetickou indukci určujeme, rovná vzdálenosti obou vodičů.

Toto platí analogicky i pro druhý vodič, který se nachází v magnetickém poli prvního vodiče, ten na něj tedy také působí magnetickou silou.

Směr sil, kterými na sebe oba vodiče navzájem působí, určíme pomocí Flemingova pravidla levé ruky.
Řešení a) Souhlasný směr proudu
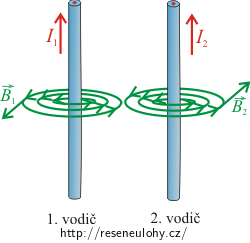
V okolí obou vodičů, kterými prochází elektrické proudy, se vytváří magnetická pole charakterizovaná magnetickou indukcí. Směry vektorů magnetických indukcí určíme pomocí Ampérova pravidla pravé ruky.

První vodič s proudem se nachází v magnetickém poli vytvořeném druhým vodičem. Na první vodič tedy působí magnetická síla, pro jejíž velikost platí
\[F_2=B_2I_1l,\tag{1}\]
kde B₂ je velikost magnetické indukce magnetického pole vytvořeného druhým vodičem v místě prvního vodiče a I₁ je velikost proudu, který prochází prvním vodičem.

Pro velikost vektoru magnetické indukce B₂ platí vztah
\[B_2= \frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_2}{R},\]
kde R je vzdálenost místa, ve kterém velikost magnetické indukce určujeme. V našem případě je to v místě, kde se nachází druhý vodič. Vzdálenost R tedy odpovídá vzdálenosti vodičů.

Vztah pro velikost magnetické indukce B₂ dosadíme do rovnice pro velikost magnetické síly F₂ a upravíme:
\[F_\mathrm{2}=\frac{\mu_\mathrm{o}}{2\pi}\,\frac{I_1I_2}{R}l. \]
Získali jsme tak vztah pro velikost magnetické síly F₂, kterou působí druhý vodič s proudem na první.

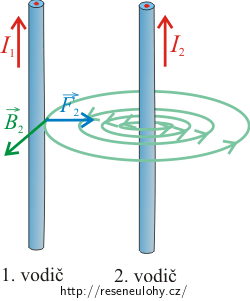
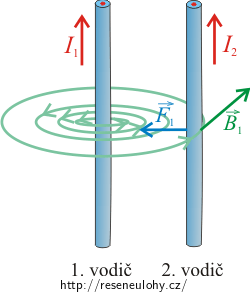
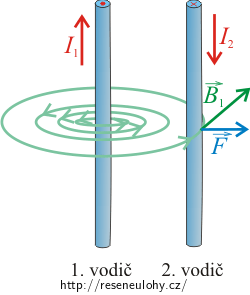
Směr magnetické síly určíme pomocí Flemingova pravidla levé ruky. V našem případě má magnetická síla \(\vec{F}_2\), kterou působí druhý vodič na první, směr doprava.

Poznámka: Na obrázku je pro přehlednost znázorněno pouze magnetické pole vytvořené druhým vodičem, protože díky němu působí druhý vodič na první magnetickou silou \(\vec{F}_2\).

Stejně i na druhý vodič, který se nachází v magnetickém poli prvního vodiče, působí magnetická síla. Pro její velikost platí
\[F_1=B_1I_2l,\]
kde B₁ je velikost magnetické indukce magnetického pole vytvořeného prvním vodičem a I₂ je velikost proudu procházející druhým vodičem.

Pro velikost vektoru magnetické indukce B₁ platí vztah
\[B_1= \frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_1}{R},\]
který dosadíme do rovnice pro velikost magnetické síly F₁:
\[F_1=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_1I_2}{R}l.\]
Směr vektoru magnetické síly \(\vec{F}_1\) určíme také pomocí Flemingova pravidla levé ruky. Síla, kterou působí první vodič na druhý, má v našem případě směr doleva.

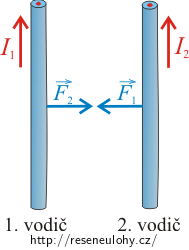
Síly \(\vec{F}_1\) a \(\vec{F}_2\), kterými na sebe navzájem působí vodiče s proudem, mají stejnou velikost. Označme si tuto společnou hodnotu F:
\[F_1=F_2=F=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_1I_2}{R}l.\]
Vodiče s proudem tedy na sebe působí silami stejné velikosti, ale opačného směru. Pokud si uvědomíme znění 3. Newtonova zákona (zákon akce a reakce), tak jsme k tomuto závěru mohli dospět přímo a nemuseli jsme určovat směr a velikost druhé síly.

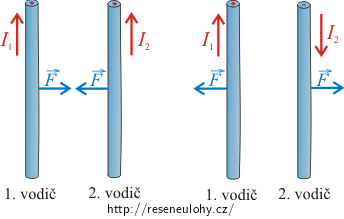
Pokud vodiči prochází elektrické proudy ve stejném směru, tak se vodiče přitahují.
Řešení b) Nesouhlasný směr proudu
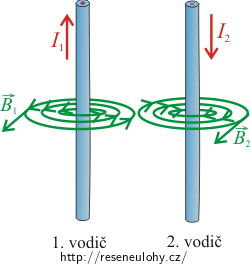
V okolí vodičů, jimiž prochází elektrické proudy, se vytvoří magnetická pole charakterizovaná magnetickou indukcí, jejíž směry určíme pomocí Ampérova pravidla pravé ruky.

Při změně směrů proudů ve vodičích se změní pouze směry magnetických indukcí a směry působících sil. Velikosti magnetických sil působících na vodiče však budou stejné jako v případě, kdy vodiči procházely proudy v souhlasném směru. Pro velikost magnetické síly působící na každý z vodičů platí vztah odvozený v Řešení a):
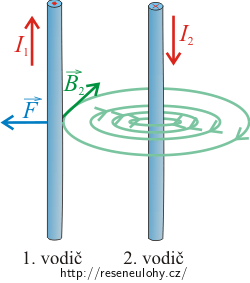
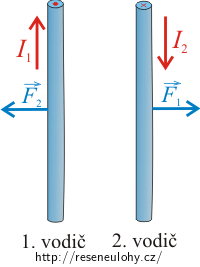
\[F=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_1I_2}{R}l.\]
Směr magnetické síly působící na první vodič určíme pomocí Flemingova pravidla levé ruky. V našem případě má magnetická síla, kterou působí druhý vodič na první, směr doleva.

Směr magnetické síly působící na druhý vodič určíme také pomocí Flemingova pravidla levé ruky. Síla, kterou působí první vodič na druhý, má v našem případě směr doprava.

Vodiče tedy na sebe působí stejně velkými silami, které mají opačný směr, což souhlasí se 3. Newtonovým zákonem (zákon akce a reakce).

Pokud vodiči prochází proudy v různých směrech, vodiče se odpuzují.
Shrnutí
Pokud rovnoběžnými vodiči prochází elektrické proudy, velikosti sil, kterými na sebe vodiče vzájemně působí, jsou stejné a platí pro ně vztah
\[F=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_1I_2}{R}l.\]
Směry proudů ve vodičích ovlivní pouze směry magnetických sil a to tak, že pokud vodiči prochází elektrické proudy stejným směrem, vodiče se navzájem přitahují. Pokud vodiči procházejí opačně orientované proudy, vodiče se odpuzují.

Zápis a číselné dosazení

\(I_1\,=10\,\mathrm{A}\)	proud tekoucí prvním vodičem
\(I_2\,=20\,\mathrm{A}\)	proud tekoucí druhým vodičem
\(R\,=\,10\,\mathrm{cm}=0{,}10\,\mathrm{m}\)	vzdálenost vodičů
\(l\,=\,1\,\mathrm{m}\)	délka vodiče
\(F\,=\,?\)	síla, která působí na vodič délky l
Z tabulek:
\(\mu_\mathrm{0}=4\pi \cdot 10^{-7}\,\mathrm{Hm^{-1}}\)	permeabilita vakua

\[F=\frac{\mu_\mathrm{0}}{2\pi}\,\frac{I_1I_2}{R}\,l=\frac{4\cdot\pi \cdot 10^{-7}}{2\cdot\pi}\cdot\,\frac{10{\cdot} 20}{0{,}1}\cdot1\,\mathrm{N}=4{\cdot} 10^{-4}\,\mathrm{N}=0{,}4\,\mathrm{mN}\]

Odpověď
Velikost sil, kterými na sebe oba vodiče vzájemně působí, nezáleží na směru proudů ve vodičích a má pro oba případy velikost 0,4 mN.

Pokud vodiči prochází elektrické proudy stejným směrem, vodiče se vzájemně přitahují.

V případě, že vodiči prochází proudy v opačných směrech, vodiče se odpuzují.
Komentář – Definice ampéru
Na základě získaného vztahu pro velikost magnetické síly, kterou na sebe navzájem vodiče působí, je definovaná jednotka proudu ampér, která je jednou ze sedmi základních jednotek soustavy SI.
Definice ampéru
Jeden ampér je stály proud, který při průchodu dvěma přímými rovnoběžnými nekonečně dlouhými vodiči zanedbatelného průřezu umístěnými ve vakuu ve vzdálenosti 1 m od sebe vyvolá mezi vodiči sílu o velikosti 2·10^-7 N na 1 m délky vodiče.
Související experiment
Experiment zabývající se stejnou problematikou: Vzájemné působení vodičů s proudem.