Výpočet silového momentu působícího na cívku vzhledem k její ose otáčení
Úloha číslo: 69
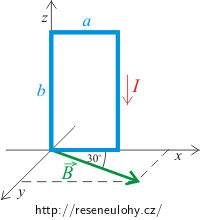
Obdélníková cívka má 20 závitů a protéká jí elektrický proud 0,1 A. Strany cívky mají délku 10 cm a 5 cm. Osa, kolem níž se může cívka otáčet, je totožná s jednou její delší stranou a označíme ji jako osu z (viz obrázek). Magnetické pole má velikost 0,5 T. Vektor \(\vec{B}\) je rovnoběžný s rovinou xy a s osou x svírá úhel 30°. Určete velikost a směr silového momentu působícího na cívku vzhledem k její ose otáčení.
Nápověda
Uvědomte si, na čem závisí a jak vypadá vztah pro moment síly působící na vodivou smyčku v magnetickém poli.
Rozbor
Na cívku, kterou protéká proud, působí magnetické pole momentem síly, který vypočítáme jako vektorový součin magnetického dipólového momentu cívky a magnetické indukce působící na cívku.
Směr magnetického dipólového momentu je dán pravidlem pravé ruky a jeho velikost závisí přímo úměrně na počtu závitů cívky, obsahu plochy jednoho závitu cívky a proudu, který jí protéká.
Řešení - pomocí magnetického momentu cívky
Na cívku s magnetickým momentem \(\vec{\mu}\) působí magnetické pole o indukci \(\vec{B\,}\) momentem síly \(\vec{M\,}\):
\[\vec{M\,} = \vec{\mu\,}\times \vec{B\,}.\]Velikost momentu síly si můžeme vyjádřit pomocí vlastností vektorového součinu:
\[M=\mu B \sin{\alpha},\]kde úhel α je úhel mezi vektory magnetického dipólu \(\vec{\mu}\) a magnetickou indukcí \(\vec{B}\).
Směr magnetického dipólového momentu \(\vec{\mu}\) je dán pravidlem pravé ruky, kde zahnuté prsty ukazují směr proudu a vztyčený palec směr magnetického dipólového momentu \(\vec{\mu}\).
Velikost μ je definována vztahem:
\[\mu = NIS.\]Vztah pro magnetický dipólový moment μ dosadíme do rovnice pro velikost momentu síly:
\[M= NISB \sin{ \alpha}.\]Směr magnetického dipólového momentu určíme z vektorového součinu \( \vec{\mu\,}\times \vec{B\,}\). Magnetický dipólový moment je kolmý na tento vektorový součin. Směr určíme pomocí pravidla pravé ruky, které říká, že vztyčený palec pravé ruky ukazuje směr \( \vec{\mu}\times \vec{B\,}\), jestliže zahnuté prsty ukazují sklopení vektru \( \vec{\mu}\) do vektoru \( \vec{B\,}\).
Vektror \( \vec{\mu}\) má totožný směr s normálou plochy smyčky. Její směr určíme pomocí pravidla pravé ruky, kde zahnuté prsty představují směr proudu a vztyčený palec směr normály plochy. Normálový vektor plochy a tedy i magnetický dipólový moment míří v záporném směru osy y.
Výsledný moment síly \( \vec{M\,}\) míří v záporném směru osy z (směrem dolů).
Zápis a číselné dosazení
\(N = 20\) počet závitů obdélníkové cívky \(a = 5\,\mathrm{cm}= 0{,}05\,\mathrm{m}\) první rozměr obdélníkové cívky \(b = 10\,\mathrm{cm}=0{,}1\,\mathrm{m}\) druhý rozměr obdélníkové cívky \(I = 0{,}10 \,\mathrm{A}\) proud protékající cívkou \(B = 0{,}5 \,\mathrm{T}\) velikost magnetického pole cívky \(\alpha = 120^{\mathrm{\circ}}\) úhel mezi vektory magnetického dipólu a magnetickou indukcí \(M\,=\,?\,\mathrm{(Nm)}\) velikost silového momentu působícího na cívku vzhledem k její ose otáčení
\[M= NISB \sin{\alpha} = NIBab \sin{\alpha}=\left({20{\cdot} 0{,}1 {\cdot}0{,}5{\cdot} 0{,}10{\cdot} 0{,}05\cdot \sin 120^{\mathrm{\circ}}}\right)\,\mathrm{Nm} = 4{,}3 \,\mathrm{mNm}\]Odpověď
Silový moment působící na cívku vzhledem k její ose otáčení směřuje v záporném směru osy z a jeho velikost je M = 4,3 mNm.Komentář - řešení pomocí sil
Celkový moment vyjádříme jako součet momentů sil na jednotlivé úseky cívky. Pro moment síly platí:
\[\vec{M} = \vec{r}\times \vec{F}.\]Velikost momentu síly si můžeme vyjádřit pomocí vlastností vektorového součinu:
\[M=rF\sin{\alpha},\]kde r je vzdálenost od osy otáčení, F je magnetická síla působící na rameno r a α úhel, který svírají.
Směr magnetické síly \(\vec{F}\) určíme podle Flemingova pravidla levé ruky, kde prsty ukazují směr proudu ve vodiči, magnetické indukční síly vstupují do dlaně a palec ukazuje směr síly.
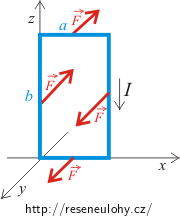
Z obrázku vidíme, že silový moment působící na stranu splývající s osou z je nulový, protože vzdálenost strany vůči ose je nulová. Pro určení silových momentů působících na kratší strany cívky (kolmé na osu otáčení) nejprve určíme směr sil. Magnetické síly působící na tyto dvě části cívky mají stejnou velikost, ale opačný směr. Ten budou mít i silové momenty. Celkový moment od těchto dvou částí vodiče se tedy ruší. Do celkového momentu přispěje pouze moment síly působící na stranu rovnoběžnou s osou.
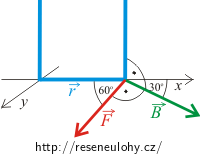
Protože je vodič kolmý na magnetickou indukci B, magnetická síla, která působí na vodiče, je:
\[F = NBbI.\]Jelikož se jedná o cívku s N závity, vynásobili jsme sílu počtem závitů N.
Vzdálenost vodiče od osy otáčení je rovna kratší straně a.
Úhel α je úhel mezi \(\vec{r}\) (vektor mířící od osy k vodiči) a magnetickou sílou \(\vec{F}\) a je roven 120°.
Po dosazení do vzorce pro moment sil dostáváme:
\[M = abNBI\sin{\alpha}.\]Všimněte si, že vyšel stejný vztah, jako když jsme silový moment počítali pomocí magnetického momentu cívky.
Směr momentu sil určíme z rovnice pro moment síly:
\[\vec{M} = \vec{r}\times \vec{F}.\]Vektorový součin \(\vec{r}\times \vec{F}\) je kolmý na oba vektory \( \vec{r}\) a \(\vec{F}\). Pravidlo pravé ruky nám říká, že vztyčený palec pravé ruky ukazuje směr \(\vec{r}\times \vec{F}\), jestliže zahnuté prsty ukazují sklopení vektoru \(\vec{r}\) do vektoru \(\vec{F}\).
Vektor \(\vec{r}\) míří v našem případě v kladném směru osy x. Moment sil \(\vec{M\,}\) bude tedy směřovat dolů.

