Sbírka řešených úloh

Určení znaménka dvou bodových nábojů II

Úloha číslo: 1019

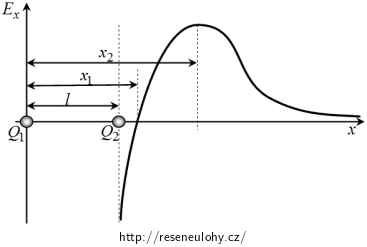
Dva bodové náboje Q₁, Q₂ jsou umístěny ve vzdálenosti l od sebe. Na obrázku je závislost E_x na x. Určete znaménka a poměr velikostí nábojů, víte-li, že intenzita je nulová v bodě ve vzdálenosti x₁ od náboje Q₁. Dále určete vzdálenost x₂, v níž je velikost intenzity maximální.

Poznámka: \(E_\mathrm{x} > 0\), je-li orientována vpravo, a \(E_\mathrm{x} < 0\), je-li orientována vlevo.

• Nápověda

  Jaká je závislost intenzity na vzdálenosti od bodového náboje?

  Co vám o daném náboji řekne jeho intenzita?

• Řešení nápovědy

  Velikost intenzity bodového náboje E klesá se čtvercem vzdálenosti x od tohoto náboje podle vztahu \[E=\frac{1}{4\pi\epsilon_0}\frac{Q}{x^2},\] kde ε₀ je permitivita vakua (permitivita vzduchu je velmi blízká permitivitě vakua), Q je velikost náboje, v jehož okolí chceme počítat elektrickou intenzitu E, a x je vzdálenost od tohoto bodového náboje.

  Dále víme, že náboj je kladný, směřuje-li vektor intenzity od něj, a záporný, směřuje-li tento vektor k němu.

• Rozbor

  Víme, že náboj je kladný, směřuje-li vektor intenzity od něj, a záporný, směřuje-li tento vektor k němu. Na základě této informace a poznámky v zadání určíme znaménko náboje Q₂.

  V bodě ve vzdálenosti x₁ od náboje Q₁ je celková intenzita rovna nule. To znamená, že velikosti intenzit od obou nábojů se v tomto bodě rovnají.

  K určení vzdálenosti, kde je intenzita maximální, použijeme funkční závislost velikosti celkové intenzity na vzdálenosti od náboje Q₁. Poté určíme extrém této funkce.

• Řešení

  Víme, že náboj je kladný, směřuje-li vektor intenzity od něj, a záporný, směřuje-li tento vektor k němu. Z grafu vidíme, že intenzita směřuje k náboji Q₂, a proto je náboj Q₂ záporný.

  O něco složitější je určení znaménka druhého náboje, protože neznáme průběh intenzity v jeho okolí. Kdyby měl tento náboj stejné znaménko jako Q₂, měly by intenzity elektrických polí obou nábojů vpravo od náboje Q₁ stejný směr. V takovém případě by však v žádném bodě ležícím napravo od náboje Q₁ nemohla být celková intenzita elektrického pole nulová, což podle grafu v zadání zjevně je. Náboj Q₁ tedy musí být kladný.

  V bodě ve vzdálenosti x₁ od náboje Q₁ je celková intenzita rovna nule. To znamená, že velikost intenzity obou nábojů je v tomto bodě stejná: \[ E_1=E_2.\] Dosadíme vztah pro intenzitu uvedený v nápovědě:

  \[ \frac{1}{4\pi\epsilon_0}\frac{Q_1}{x^2_1}=\frac{1}{4\pi\epsilon_0}\frac{Q_2}{(x_1-l)^2} \] a vyjádříme poměr velikostí obou nábojů: \[ \frac{Q_1}{Q_2}=\left(\frac{x_1}{x_1-l}\right)^2. \]

  Nyní nám již zbývá pouze určit, ve kterém bodě bude intenzita maximální. Proto určíme závislost velikosti celkové intenzity E na vzdálenosti x od náboje Q₁. Vzhledem k tomu, že náboje mají opačné znaménko a bod, ve kterém intenzitu počítáme, leží na jejich spojnici, velikost celkové intenzity E určíme jako rozdíl velikostí intenzit od prvního náboje E₁ a od druhého náboje E₂ (toto platí vpravo od druhého náboje, tj. pro x > l, což je oblast, ve které hledáme maximum):

  \[ E=E_1-E_2=\frac{1}{4\pi\epsilon_0}\frac{Q_1}{x^2}-\frac{1}{4\pi\epsilon_0}\frac{Q_2}{(x-l)^2}=\frac{1}{4\pi\epsilon_0}\left [\frac{Q_1}{x^2}-\frac{Q_2}{(x-l)^2}\right ]. \]

  Hledáme maximum této funkce. To znamená, že ji zderivujeme a derivaci položíme rovnu nule:

  \[ \frac{\mathrm dE}{\mathrm dx}=\frac{1}{4\pi\epsilon_0}\left[\frac{-2Q_1}{x^3}-\frac{-2Q_2}{(x-l)^3}\right]=0.\]

  Nyní výraz upravíme a dostáváme rovnici \[\frac{Q_1}{x^3}=\frac{Q_2}{(x-l)^3}.\] Odtud vyjádříme vzdálenost x: \[\frac{Q_2}{Q_1}=\frac{(x-l)^3}{x^3}\] \[\frac{x-l}{x}=\sqrt[3]{\frac{Q_2}{Q_1}}\] \[1-\frac{l}{x}=\sqrt[3]{\frac{Q_2}{Q_1}}\] \[-\frac{l}{x}=\sqrt[3]{\frac{Q_2}{Q_1}}-1\] \[x=\frac{l}{1-\sqrt[3]{\frac{Q_1}{Q_2}}}.\]

  Určili jsme vzdálenost x, která už je hledanou vzdáleností x₂.

• Odpověď

  Náboj Q₂ je záporný a Q₁ kladný.

  Poměr velikostí nábojů je \(\frac{Q_1}{Q_2}=\left(\frac{x_1}{x_1-l}\right)^2\).

  Vzdálenost, ve které je intenzita maximální, je dána vztahem \[x_2=\frac{l}{1-\sqrt[3]{\frac{Q_1}{Q_2}}}. \]

• Průběh elektrické intenzity podél osy x

  

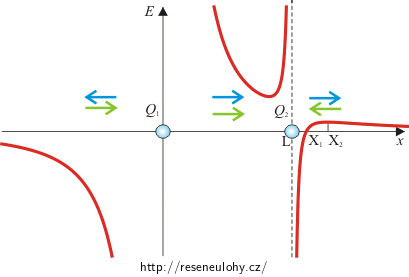
  Graf celkové intenzity je sestrojen tak, že v průsečíku os se nachází náboj Q₁ a v bodě L desetkrát menší náboj Q₂. Body X₁ (průsečík grafu s osou x) a X₂ (lokální maximum) znázorňují vzdálenosti uvedené v zadání. Část grafu vpravo od bodu L odpovídá grafu v zadání, který je sestrojen v jiném měřítku, proto by se na první pohled mohlo zdát, že si grafy neodpovídají. Šipky v grafu znázorňují směr, ale ne velikost elektrických intenzit obou nábojů v jednotlivých úsecích. Modré šipky znázorňují intenzitu náboje Q₁ a zelené intenzitu náboje Q₂.