Magnetické pole solenoidu s vodičem
Úloha číslo: 59
Dlouhým solenoidem ležícím ve vakuu s hustotou 10 závitů na centimetr a poloměrem 7 cm protéká proud 20 mA. Přímým vodičem ležícím v ose solenoidu protéká proud 6 A.
V jaké vzdálenosti od osy solenoidu bude svírat vektor celkové magnetické indukce úhel 45° s osou vodiče? Jaká je v tomto místě velikost magnetické indukce B?
Nápověda
Nakreslete si, jak vypadají magnetická pole vytvořená přímým vodičem s proudem a solenoidem.
Co musí platit pro oba příspěvky, aby požadovaný úhel byl 45°?
Obrázek
Kolmý řez solenoidem:

Zeleně jsou indukční čáry pole solenoidu, modře indukční čáry pole přímého vodiče.
Podélný řez solenoidem
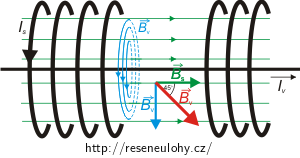
Zeleně jsou indukční čáry pole solenoidu, modře indukční čáry pole přímého vodiče.
Pozn.: Jedná se o velmi dlouhý solenoid, na obrázku je znázorněna pouze jeho část. Závity jsou po celé délce solenoidu, pro přehlednost nejsou uprostřed nakresleny, aby bylo „vidět dovnitř“.
Rozbor
Protože solenoidem i dlouhým vodičem protéká proud, tvoří se v jejich okolí magnetická pole.
Uvnitř solenoidu je magnetické pole rovnoběžné s osou. V našem případě rovnoběžné i s vodičem, který prochází solenoidem (viz obrázek). Magnetické pole vodiče tvoří soustředné kružnice se středem ve vodiči. Z toho plyne, že magnetické indukce solenoidu a vodiče jsou na sebe vždy kolmé.
Aby vektor výsledné magnetické indukce svíral s osou solenoidu, tedy i s magnetickou indukcí, úhel 45°, musí být oba příspěvky stejně velké. Velikost magnetické indukce uvnitř solenoidu nezávisí na poloze (je konstantní). Magnetická indukce dlouhého vodiče klesá se vzdáleností od vodiče. Naším úkolem je tedy najít takovou vzdálenost od vodiče, kde se velikost magnetické indukce vodiče bude rovnat velikosti magnetické indukce solenoidu.
Řešení
Pro velikost magnetické indukce dlouhého vodiče Bv platí vztah
\[B_\mathrm{v}=\frac{\mu_0I_\mathrm{v}}{2\pi R},\]kde Iv je proud, který vodičem protéká, a R vzdálenost mezi vodičem a místem, kde určujeme magnetickou indukci.
Pro velikost magnetické indukce solenoidu Bs platí
\[B_\mathrm{s}=\mu_0I_\mathrm{c}n,\]kde Is je proud, který solenoidem protéká, n hustota závitů a μ0 permeabilita vakua.
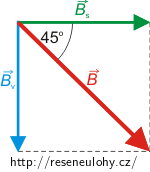
Jak bylo vysvětleno v rozboru a je vidět i na obrázcích, výsledná magnetická indukce B bude svírat s osou solenoidu úhel 45°, jestliže bude platit
\[B_\mathrm{v}=B_\mathrm{s}.\]Za Bv a Bs dosadíme výše uvedené vztahy
\[\frac{\mu_0I_\mathrm{v}}{2\pi R}=\mu_0I_\mathrm{c}n.\]Z této rovnice vyjádříme neznámou vzdálenost R:
\[R=\frac{I_\mathrm{v}}{2\pi I_\mathrm{c}n}.\]Velikost celkové magnetické indukce ve vzdálenosti R od osy vodiče vypočítáme jako (viz obrázek):
\[B = \frac{B_\mathrm{s}}{\cos 45^{\circ}}.\]Zápis a číselné dosazení
\(n=10\,\mathrm{cm^{-1}}=1000\,\mathrm{m^{-1}}\) hustota závitů solenoidu \(r=7\,\mathrm{cm}=0{,}070\,\mathrm{m}\) poloměr solenoidu \(I_\mathrm{c} =20\,\mathrm{mA}=0{,}020\,\mathrm{A}\) proud tekoucí solenoidem \(I_\mathrm{v} =6\,\mathrm{A}\) proud tekoucí přímým vodičem \(R=?\,\mathrm{(cm)}\) vzdálenost od osy solenoidu, ve které osa vodiče a vektor mg. indukce svírají úhel 45° \(B=?\,\mathrm{(B)}\) velikost magnetické indukce
\[R=\frac{I_\mathrm{v}}{2\pi I_\mathrm{c}n}=\frac{6}{2\pi\cdot0{,}02{\cdot}1000}\,\mathrm{m}=0{,}048\,\mathrm{m}=4{,}8\,\mathrm{cm}\] \[B=\frac{B_\mathrm{s}}{\cos45^{\circ}}=\frac{\mu_0I_\mathrm{c}n}{\cos45^{\circ}}=\dfrac{4\pi\cdot10^{-7}\cdot0{,}02{\cdot}1000}{\dfrac{\sqrt{2}}{2}}\,\mathrm{Tv}\dot{=} 3{,}554{\cdot}10^{-5}\,\mathrm{T} \,\dot{=}\, 36\,\mathrm{\mu T}\]Odpověď
Vektor výsledné magnetické indukce B bude svírat úhel 45° ve vzdálenosti R = 4,8 cm od osy solenoidu. V tomto místě je velikost celkové magnetické indukce přibližně B = 36 μT.




