Metody řešení lineárních obvodů 1
Úloha číslo: 1812
Tato úloha slouží jako modelová, jsou zde vysvětleny metody řešení složitějších lineárních obvodů stejnosměrného proudu.
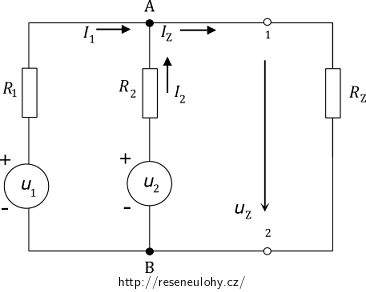
Na obrázku je nakresleno schéma zapojení se třemi rezistory \(R_1 = 5\,\Omega\), \(R_2=10\,\Omega\), \(R_\mathrm{Z} = 10\,\Omega\) a dva stejnosměrné zdroje napětí \(U_1 = 10\,V\), \(U_2 = 12\,V\).
Řeště tento obvod pomocí:
a) metody smyčkových proudů. Určete proudy jednotlivými rezistory \(I_1\), \(I_2\) a \(I_\mathrm{Z}\).
b) metody uzlových napětí. Určete uzlové napětí \(U_\mathrm{A}\) a proudy jednotlivými rezistory \(I_1\), \(I_2\) a \(I_\mathrm{Z}\).
c) metody lineární superpozice. Určete napětí na rezistoru \(U_\mathrm{Z}\).
d) Théveninovy věty. Určete napětí na rezistoru \(U_\mathrm{Z}\).
Připomenutí Kirchhoffových zákonů
Všechny metody, které se v úloze používají, vycházejí z Kirchhoffových zákonů, proto si je připomeňme.
První Kirchhoffův zákon je vlastně zákon zachování elektrického náboje a říká:
- v každém bodě (uzlu) elektrického obvodu platí, že součet proudů vstupujících do uzlu se rovná součtu proudů z uzlu vystupujících.
Druhý Kirchhoffův zákon vychází z konzervativnosti elektrického pole a říká:
- součet úbytků napětí na spotřebičích se v uzavřené části obvodu (smyčce) rovná součtu elektromotorických napětí zdrojů v této části obvodu (smyčce);
nebo
- algebraický součet napětí ve smyčce je roven nule.
První výše uvedené znění II. Kirchhoffova zákona se uplatňuje v úlohách, ve kterých se Kirchhoffovy zákony používají pro řešení obvodů s více zdroji a které doporučujeme těm, co si chtějí jejich použití připomenout, např. úloha Použití Kirchhoffových zákonů pro řešení obvodu se dvěma zdroji. Ve druhém znění tohoto zákona je třeba uvažovat napětí na zdroji s opačným znaménkém, než má jeho elektromotorické napětí. Toto znění se používá na školách s technickým zaměřením, kde se také častěji používají zde použité metody řešení obvodů. Proto v této úloze a v úlohách na ni navazujících používáme toto znění.
a) Rozbor – metoda smyčkových proudů
Metoda řešení obvodů pomocí smyčkových proudů usnadňuje a zrychluje výpočty elektrických obvodů. Její princip vychází z Kirchhoffových zákonů a zavádí novou, neznámou veličinu, tzv. smyčkový proud. Označíme si tedy proudy jednotlivými smyčkami v obvodu (místo označení proudů větvemi). Pro každou smyčku sestavíme rovnice podle II. Kirchhoffova zákona — proud každým prvkem je součtem proudů všemi smyčkami, do kterých daný prvek patří. Ze smyčkových hodnot proudů se poté určí pomocí I. Kirchhoffova zákona proudy jednotlivými větvemi obvodu.
a) Postup řešení
Naším úkolem je určit poudy I1, I2 a IZ :
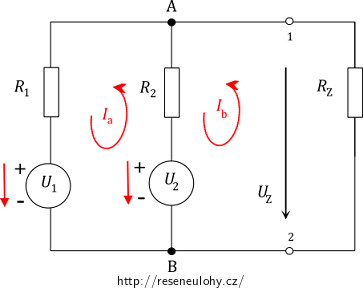
1. U zdrojů napětí si vyznačíme šipkou (na obrázku červeně) směr napětí. Pozor, jeho směr je opačný než směr elektromotorického napětí (viz poznámka v prvním oddíle této úlohy).
2. Zvolíme uzavřené smyčky a jejich směr, proudy smyčkou nazveme Ia, Ib.
3. Napíšeme rovnice pro jednotlivé smyčky. Místo proudů I1, I2, IZ budeme dosazovat smyčkové proudy Ia, Ib.
4. Vyřešíme získané rovnice, tj. spočítáme neznámé smyčkové proudy Ia a Ib.
5. Ze smyčkových proudů Ia, Ib určíme reálné proudy I1, I2, IZ.
a) 1. část řešení – sestavení a vyřešení rovnic

Pomocí druhého Kirchhoffova zákona napíšeme rovnici pro smyčku a:
\[R_1I_\mathrm{a} + R_2(I_\mathrm{a}-I_\mathrm{b})+ U_1-U_2 \,=\,0.\tag{smyčka a}\]Rezistor R2 patří do smyčky a i do smyčky b, proto je třeba při výpočtu úbytku napětí uvažovat oba smyčkové proudy. Znaménka udávají směry smyček. Po úpravě dostaneme:
\[I_\mathrm{a}(R_1 + R_2)-R_2I_\mathrm{a}\,=\, U_2-U_1.\]A obdobně pro smyčku b:
\[R_2(I_\mathrm{b}-I_\mathrm{a}) + R_\mathrm{Z}I_\mathrm{b}+U_2\,=\,0,\tag{smyčka b}\] \[I_\mathrm{b}(R_2+R_\mathrm{z})- R_2I_\mathrm{a}\,=\,- U_2.\]Nyní máme dvě rovnice o dvou neznámých. Dosadíme do nich zadané hodnoty v základních jednotkách:
\[15I_\mathrm{a} - 10I_\mathrm{b}\,=\,2,\] \[-10I_\mathrm{a} + 20I_\mathrm{b}\,=\,-12. \]Soustavu vyřešíme, například sčítací metodou. První rovnici vynásobíme dvěma:
\[30I_\mathrm{a} - 20I_\mathrm{b}\,=\,4, \] \[-10I_\mathrm{a} + 20I_\mathrm{b}\,=\,-12\]a přičteme ke druhé rovnici:
\[20I_\mathrm{a}\,=\,-8. \]Tím jsme se zbavili neznámé Ib a vypočítáme Ia:
\[I_\mathrm{a}\,=\, -\frac{2}{5}\,\mathrm{A}.\]Nyní dopočítáme i proud Ib:
\[15 (-\frac{2}{5})\, -10I_\mathrm{b}\,=\,2, \] \[I_\mathrm{b}\,=\, -\frac{4}{5}\,\mathrm{A}.\]Smyčkové proudy nám vyšly záporné, což znamená, že proud teče opačným směrem, než zvolený směr smyčky.
a) 2. část řešení – určení reálných proudů
Nyní potřebujeme určit hodnoty reálných proudů pomocí smyčkových proudů. Použijeme jejich vyjádření pomocí smyčkových proudů:
\[I_1\,=\,-I_\mathrm{a} \Rightarrow\, I_1\,=\,\frac{2}{5}\,\mathrm{A}, \] \[I_\mathrm{z}\,=\,-I_\mathrm{b} \Rightarrow\, I_\mathrm{z}\,=\,\frac{4}{5}\,\mathrm{A}, \] \[I_2\,=\,I_\mathrm{z}-I_1 \Rightarrow\, I_2\,=\,\left(\frac{4}{5}\,-\frac{2}{5}\right)\,\mathrm{A}\, \Rightarrow\, I_2\,=\,\frac{2}{5}\,\mathrm{A}.\]a) Odpověď
Spočítali jsme smyčkové proudy \(I_\mathrm{a}\) a \(I_\mathrm{b}\):
\[I_\mathrm{a}\,=\, -\frac{2}{5}\,\mathrm{A},\qquad \ I_\mathrm{b}\,=\, -\frac{4}{5}\,\mathrm{A}. \]Ze smyčkových proudů jsme určili proudy reálné — \(I_1\), \(I_2\) a \(I_\mathrm{Z}\):
\[I_1\,=\, -\frac{2}{5}\,\mathrm{A},\qquad \ I_2\,=\, -\frac{2}{5}\,\mathrm{A},\qquad \ I_\mathrm{Z}\,=-\, \frac{4}{5}\,\mathrm{A}. \]b) Rozbor – metoda uzlových napětí
Metoda řešení elektrických obvodů pomocí uzlových napětí usnadňuje a zrychluje výpočty především tam, kde se vyskytují proudové zdroje. Její princip vychází z Kirchhoffových zákonů a zavádí nové veličiny tzv. uzlové napětí a referenční uzel.
Jeden vhodně zvolený uzel (nejvýhodnější je ten, ve kterém je spojeno nejvíce prvků) označíme jako uzel referenční. Napětí každého z ostatních uzlů vztahujeme k uzlu referenčnímu a označujeme jako uzlové napětí. Proudy v prvcích obvodu potom vyjádříme pomocí rozdílu uzlových napětí.
Poznámka: Lze na to také nahlížet tak, že v referenčním uzlu je nulový potenciál a uzlové napětí je vlastně potenciálem v daném uzlu při této volbě nulového potenciálu.
b) Postup řešení
Naším úkolem je určit poudy I1, I2 a IZ:
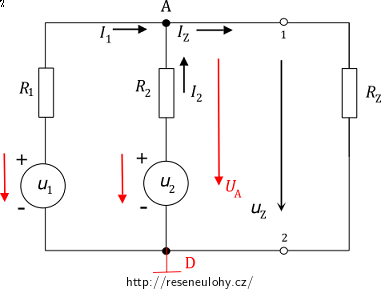
1. U zdrojů napětí si vyznačíme šipkou směr napětí.
2. V zapojení si vyznačíme jednotlivé uzly (A, D) a jeden z nich označíme jako uzel referenční (v této úloze zvolíme uzel D, uzel A to být nemůže, protože v něm máme počítat uzlové napětí). Referenční uzel volíme tak, aby k němu bylo připojeno co nejvíce prvků.
3. Uzlové napětí mezi uzlem A a referenčním uzlem D označíme jako UA.
4. Napíšeme I. Kirchhoffův zákon pro uzel A.
5. Proudy v jednotlivých prvcích obvodu vyjádříme pomocí uzlových napětí, napětí zdrojů a odporů rezistorů. Získáme tím soustavu rovnic.
6. Řešením rovnic získáme uzlové napětí.
7. Pomocí uzlového napětí dopočítáme proudy v obvodu.
b) Řešení – sestavení a vyřešení rovnic

Napíšeme rovnici podle I. KZ pro uzel A:
\[I_1 + I_2 - I_\mathrm{z}\,=\,0 \Rightarrow\, I_1 + I_2 \,=\,I_\mathrm{z}. \tag{uzel A}\]Proudy vyjádříme pomocí uzlového napětí UA, což je vlastně napětí mezi uzlem A a referenčním uzlem D:
\[I_\mathrm{1}\,=\, \frac{U_1-U_\mathrm{A}}{R_1}\,,\] \[I_\mathrm{2}\,=\, \frac{U_2-U_\mathrm{A}}{R_2}\,,\] \[I_\mathrm{z}\,=\,\frac{U_\mathrm{A}}{R_\mathrm{z}}.\]Tyto vztahy dosadíme do výše napsaného I. KZ pro uzel A:
\[\frac{U_1-U_\mathrm{A}}{R_1}\,+\frac{U_2-U_\mathrm{A}}{R_2}\,\,=\, \frac{U_\mathrm{A}}{R_\mathrm{z}}\,,\]kde je jediná neznámá UA, kterou vyjádříme. Vynásobením rovnice výrazem \(R_1R_2R_\mathrm{Z}\) a roznásobením závorek dostaneme:
\[U_1R_2R_\mathrm{Z}-U_\mathrm{A}R_2R_\mathrm{Z} + U_2R_1R_\mathrm{Z}-U_\mathrm{A}R_1R_\mathrm{Z} = U_\mathrm{A}R_1R_2\]a odtud plyne:
\[U_\mathrm{A} = \frac{U_1R_2R_\mathrm{Z}+U_1R_1R_\mathrm{Z}}{R_1R_2 + R_1R_\mathrm{Z} + R_2R_\mathrm{Z}}.\]Po dosazení zadaných hodnot dostaneme:
\[ U_\mathrm{A}\,=\frac{10 {\cdot} 10 \cdot 10 + 12 {\cdot}5 \cdot 10}{5 {\cdot} 10 + 5 {\cdot} 10 + 10 {\cdot} 10}\,\mathrm{A}=\,8\,\mathrm{V}.\] .Spočítali jsme uzlové napětí UA. Nyní můžeme dopočítat proudy dle vztahů uvedených výše:
\[I_\mathrm{1}\,=\, \frac{U_1-U_\mathrm{A}}{R_1}\, \Rightarrow\, I_1 \,=\, \frac{2}{5}\,\mathrm{A} ,\] \[I_\mathrm{2}\,=\, \frac{U_2-U_\mathrm{A}}{R_2}\, \Rightarrow\, I_2 \,=\, \frac{2}{5}\, \mathrm{A},\] \[I_\mathrm{z}\,=\,\frac{U_\mathrm{A}}{R_\mathrm{z}}\, \Rightarrow\, I_\mathrm{z} \,=\, \frac{4}{5}\, \mathrm{A}.\]b) Odpověď
Spočítali jsme uzlové napětí \(U_\mathrm{A}\): \[U_\mathrm{A}\,=\, 8\,\mathrm{V}.\]
Z uzlového napětí jsme určili proudy:
\[I_1\,=\, \frac{2}{5}\,\mathrm{A},\qquad \ I_2\,=\, \frac{2}{5}\,\mathrm{A},\qquad \ I_\mathrm{Z}\,=\, \frac{4}{5}\,\mathrm{A}. \]c) Rozbor – metoda lineární superpozice
Metodu lineární superpozice používáme v obvodech, ve kterých působí více zdrojů elektrické energie. Napětí nebo proud na vybraném prvku se určí tak, že necháme v obvodu zapojený jen jeden zdroj napětí nebo proudu a stanovíme napětí nebo proud na uvažovaném prvku. Ostatní zdroje napětí nahradíme jejich vnitřním odporem a zdroje proudu vyřadíme. Toto provedeme postupně pro každý zdroj. Výsledné napětí (proud) na uvažovaném prvku je potom součet napětí (proudů) vyvolaných jednotlivými zdroji samostatně.
c) Postup řešení
Naším úkolem je určit napětí UZ:
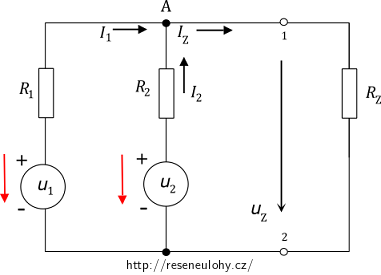
1. Vyznačíme napětí jednotlivých zdrojů.
2. Vypočteme napětí nebo proud na uvažovaném prvku při samostatném působení zdroje U1, zdroj U2 nahradíme zkratem (protože se jedná o ideální zdroj s nulovým vnitřním odporem).
3. Totéž provedeme i pro zdroj U2.
4. Výsledné napětí na uvažovaném prvku je pak dáno algebraickým součtem obou dílčích napětí.
c) 1. část řešení – uvažujeme zdroj U1
Nejprve uvažujme U1, to znamená, že zdroj U2 nahradíme zkratem (jedná se o ideální zdroj bez vnitřního odporu).
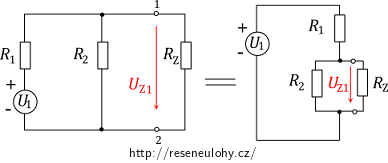
Naším úkolem je v tomto jednodušším obvodu určit napětí UZ1.
V tomto obvodu jsou rezistory R2 a RZ zapojeny paralelně a k nim je sériově připojen rezistor R1. Nejdříve spočítáme celkový odpor paralelního zapojení rezistorů R2 a RZ:
\[R_\mathrm{2Z}\,=\, \frac{R_2R_\mathrm{Z}}{R_2+R_\mathrm{Z}}.\]Celkový odpor je tedy
\[R = R_1 + R_\mathrm{2Z} = R_1 + \frac{R_2R_\mathrm{Z}}{R_2+R_\mathrm{Z}}.\]Obvodem teče proud \(\frac{U_1}{R}\). Hledané napětí UZ1 je rovno napětí na paralelním zapojení rezistorů R2 a RZ, které spočteme jako součin proudu a odporu tohoto zapojení:
\[U_\mathrm{Z1}\,= \frac{U_1}{R_1 + \frac{R_2R_\mathrm{Z}}{R_2+R_\mathrm{Z}}} \frac{R_2R_\mathrm{Z}}{R_2+R_\mathrm{Z}},\]což po úpravě dává
\[U_\mathrm{Z1}= \frac{U_1}{\frac{R_1R_2+R_1R_\mathrm{Z} + R_2R_\mathrm{Z}}{R_2+R_\mathrm{Z}}} \frac{R_2R_\mathrm{Z}}{R_2+R_\mathrm{Z}} = U_1\frac{R_2R_\mathrm{Z}}{R_1R_2+R_1R_\mathrm{Z} + R_2R_\mathrm{Z}}.\]A po dosazení zadaných hodnot dostáváme:
\[U_\mathrm{Z1}\,= 10 \cdot \frac{10{\cdot}10}{5{\cdot}10 + 5{\cdot}10 + 10{\cdot}10}\,\mathrm{V} \,=\, 5\,\mathrm{V}.\]c) 2. část řešení – uvažujeme zdroj U2
Teď uvažujme jen zdroj U2, to znamená, že zdroj U1 nahradíme zkratem (jedná se také o ideální zdroj bez vnitřního odporu).
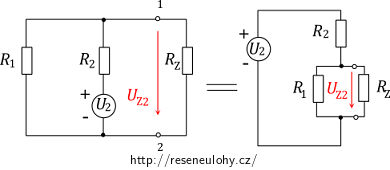
Naším úkolem je určit napětí UZ2. Budeme postupovat úplně stejně jako v předchozím oddíle. V tomto obvodu jsou rezistory R1 a RZ zapojeny paralelně a k nim je sériově připojen rezistor R2. Celkový odpor je tedy
\[R_\mathrm{1Z}\,=\, \frac{R_1R_\mathrm{Z}}{R_1+R_\mathrm{Z}},\] \[R \,=\, R_2 + \frac{R_1R_\mathrm{Z}}{R_1+R_\mathrm{Z}}. \]Obvodem teče proud \(\frac{U_2}{R}\). Hledané napětí UZ2 je rovno:
\[U_\mathrm{Z2}\,= \frac{U_2}{R_2 + \frac{R_1R_\mathrm{Z}}{R_1+R_\mathrm{Z}}} \frac{R_1R_\mathrm{Z}}{R_1+R_Z},\]což po úpravě dává
\[U_\mathrm{Z1}= \frac{U_2}{\frac{R_1R_2+R_1R_\mathrm{Z} + R_2R_\mathrm{Z}}{R_1+R_\mathrm{Z}}} \frac{R_1R_\mathrm{Z}}{R_1+R_\mathrm{Z}} = U_2\frac{R_1R_\mathrm{Z}}{R_1R_2+R_1R_\mathrm{Z} + R_2R_\mathrm{Z}}.\]A po dosazení zadaných hodnot dostáváme:
\[U_\mathrm{Z1}\,= 12 \cdot \frac{5{\cdot}10}{5{\cdot}10 + 5{\cdot}10 + 10{\cdot}10}\,\mathrm{V} \,=\, 3\,\mathrm{V}.\]Poznámka: Pokud se nad tím zamyslíme, tak se tento výpočet od výpočtu v předchozím oddíle liší jen tím, že se prohodily role zdrojů U1 a U2. Stačilo tedy vzít obecné řešení z konce předchozího oddílu a zaměnit indexy 1 a 2.
c) 3. část řešení – výsledné napětí
Nyní už máme spočítaná napětí UZ1 a UZ2, vzhledem k tomu, že v obvodu se už nevyskytuje další zdroj, tak výsledné napěti UZ je dáno součtem UZ1 a UZ2:
\[U_\mathrm{Z}\,=\, U_\mathrm{Z1}\ +U_\mathrm{Z2} = U_1\frac{R_2R_\mathrm{Z}}{R_1R_2+R_1R_\mathrm{Z} + R_2R_\mathrm{Z}} + U_2\frac{R_1R_\mathrm{Z}}{R_1R_2+R_1R_\mathrm{Z} + R_2R_\mathrm{Z}},\] \[U_\mathrm{Z}\,=\,\frac{U_1R_2R_\mathrm{Z}+U_1R_1R_\mathrm{Z}}{R_1R_2 + R_1R_\mathrm{Z} + R_2R_\mathrm{Z}} \,=\, 8\mathrm{V}.\]c) Odpověď
Postupně jsme vypočítali napětí \(U_{Z1}\) a \(U_{Z2}\) tak, že jsme v obvodu uvažovali vždy pouze jeden zdroj:
\[U_\mathrm{Z1}\,=\, 5\,\mathrm{V},\qquad \ U_\mathrm{Z2}\,=\, 3\,\mathrm{V}.\]Výsledné napětí \(U_\mathrm{Z}\) je součtem obou napětí \(U_\mathrm{Z1}\) a \(U_\mathrm{Z2}\):
\[U_\mathrm{Z}\,=\, 8\,\mathrm{V}.\]d) Rozbor – Théveniova věta
Théveninova věta o náhradním zdroji napětí tvrdí, že libovolně složitý lineární obvod lze vzhledem k libovolným dvěma uzlům nahradit obvodem skutečného zdroje napětí. Pod skutečným zdrojem si představíme ideální zdroj napětí a jeho vnitřní odpor.
To nám vlastně říká, že pokud nás zajímá jen nějaká část obvodu (jedna jeho větev), tak tu si zachováme. Určíme napětí na koncích této větve a celkový odpor zbytku obvodu vůči těmto svorkám. Zbytek obvodu potom nahradím zdrojem, jehož elektromotorické napětí bude rovno spočítanému napětí a vnitřní odpor se bude rovnat odporu zbytku obvodu.
d) Postup řešení
Naším úkolem je určit napětí UZ.

1. Ponecháme tedy větev s rezistorem RZ a zbytek obvodu nahradíme reálným zdrojem. Ekvivalentní obvod tedy vypadá takto:
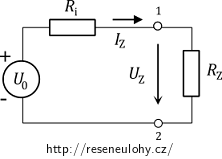
2. Vnitřní odpor Ri určíme tak, že v původním obvodu vynecháme rezistor RZ a určíme celkový odpor zbytku obvodu.
3. Dále musíme určit napětí zdroje U0, který určíme tak, že odpojíme zátěž (v našem případě rezistor Rz) a určíme napětí na výstupních svorkách.
4. V ekvivalentním obvodu již známe Ri a U0, z toho můžeme určit hledané napětí UZ.
d) 1. část řešení – vnitřní odpor Ri, napětí U0
Dle Théveninovy věty si nakreslíme ekvivalentní obvod (podrobněji v oddílech Rozbor a Postup řešení výše).

Určíme odpor Ri tak, že v původním zapojení odpojíme zátěž RZ a neuvažujeme zdroje napětí, tj. „vynecháme“ zdroje U1 a U2. Obvod si překreslíme.
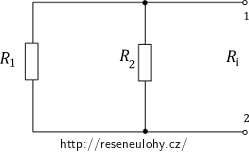
Vidíme, že jde o dva rezistory zapojené paralelně. Určíme odpor Ri:
\[R_\mathrm{i}\,=\, \frac{R_1R_2}{R_1+R_2}\,=\, \frac{50}{15}\,\mathrm{\Omega}\,\dot{=}\,3{,}33\,\mathrm{\Omega}.\]Zbývá nám určit napětí U0 na svorkách. To získáme tak, že opět odpojíme zátěž RZ a zdroje ponecháme. Obvod tedy vypadá takto:
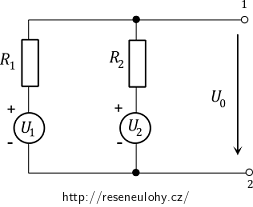
Vidíme, že i bez připojené zátěže může tímto obvodem téci proud. Ten označíme Ia a určíme ho tak, že si napíšeme II. Kirchhoffův zákon (použijeme vlastně metodu smyčkových proudů). Vyznačíme si polaritu zdrojů a směr smyčkového proudu Ia.
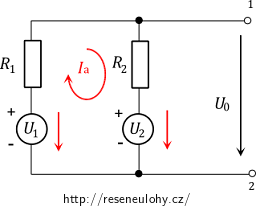
Napíšeme rovnici pro smyčku Ia:
\[R_1I_\mathrm{a} + R_2I_\mathrm{a}+U_2-U_1 \,=\,0. \]Z této rovnice spočítáme neznámý smyčkový proud Ia:
\[ I_\mathrm{a}(R_1 + R_2) \,=\,U_1-U_2, \] \[ I_\mathrm{a}\,=\,\frac{U_1-U_2}{R_1+R_2}\, \,=\,-\frac{2}{15}\, \mathrm{A}\,\dot{=}\,-0{,}13\,\mathrm{A}. \]Nyní dopočítáme napětí U0:
\[ U_0\,=\,U_2+R_2I_\mathrm{a} = U_2+R_2\frac{U_1-U_2}{R_1+R_2} = \frac{U_2R_1 + U_1R_2}{R_1+R_2}, \] \[U_0\,=\,\left(12-\frac{4}{3}\right)\,\mathrm{V} \,=\,\frac{32}{3}\,\mathrm{V}\,\dot{=}\,10{,}66\,\mathrm{V}. \]Poznámka: Pro kontrolu můžeme zkusit spočítat napětí U0 pomocí druhé části smyčky:
\[ U_0\,=\,U_1-R_1I_\mathrm{a} = U_1-R_1\frac{U_1-U_2}{R_1+R_2} = \frac{U_1R_2 + U_2R_1}{R_1+R_2} \]a vidíme, že jsme dostali stejný výsledek.
d) 2. část řešení – napětí Uz

Známe již odpor Ri a napětí U0.
Z ekvivalentního obvodu již snadno dopočítáme napětí UZ:
\[U_\mathrm{Z}\,=\, U_0\frac{R_\mathrm{Z}}{R_\mathrm{Z}+R_\mathrm{i}} = \frac{U_2R_1 + U_1R_2}{R_1+R_2}\frac{R_\mathrm{Z}}{R_\mathrm{Z}+\frac{R_1R_2}{R_1+R_2}} = \frac{U_1R_2R_Z+U_1R_1R_\mathrm{Z}}{R_1R_2 + R_1R_Z + R_2R_\mathrm{Z}}.\]Dosadíme zadané hodnoty a dostaneme:
\[U_\mathrm{Z}= \frac{10 {\cdot} 10 \cdot 10 + 12 {\cdot}5 \cdot 10}{5 {\cdot} 10 + 5 {\cdot} 10 + 10 {\cdot} 10}\,\mathrm{A}=\,8\,\mathrm{V}.\]d) Odpověď
Dle Théveninovy věty jsme si nakreslili ekvivalentní obvod. Určili jsme jeho vnitřní odpor \(R_\mathrm{i}\) a napětí \(U_0\): \[R_\mathrm{i}\,=\, \frac{50}{15}\,\mathrm{\Omega},\qquad U_0\,=\,\frac{32}{3}\,\mathrm{V}. \]
Z ekvivalentního obvodu jsme dopočítali napětí UZ:
\[U_\mathrm{Z}\,=\, 8\,\mathrm{V}.\]Komentář
V příkladu byly srovnány jednotlivé metody řešení elektrických obvodů. Vidíme, že výsledky si odpovídají.


