Vodivá tyč protékaná proudem na kolejnicích
Úloha číslo: 800
Tyč o hmotnosti 0,4 kg leží na vodorovných kolejnicích vzdálených od sebe 1 m. Kolejnicemi i tyčí protéká proud 20 A. Součinitel klidového tření mezi tyčí a kolejnicemi je 0,6. Při jaké nejmenší velikosti magnetické indukce se tyč dá do pohybu? Jaký bude směr této indukce?

Pozn. Na popsanou situaci se díváme z boku.
Nápověda 1
Uvědomte si, jaké síly na tyč působí, když se pohybuje, a zakreslete je do obrázku.
Nápověda 2 – směr magnetické síly
Hledáte minimální magnetickou indukci, takže i minimální magnetickou sílu. Magnetická síla \(\vec{F}_\mathrm{m}\) bude mířit kolmo na tyč. Předpokládejme, že magnetická síla působí tak, že svírá nějaký úhel s vodorovným směrem. Tuto sílu si pak rozložíme na část, která tyč nadlehčuje, a na část, která dává tyč do pohybu. Podrobnější vysvětlení působení magnetické síly naleznete v úloze Dívka táhne sáňky po zasněženém chodníku.
Nápověda 3
Velikost třecí síly FT, která působí na tyč, spočítáme pomocí vztahu \[F_\mathrm T=fN,\] kde f je součinitel klidového tření a N je velikost tlakové síly, kterou tlačí kolejnice na tyč.
Nápověda 4
Jak spočítáte velikost magnetické indukce? Tyč je v podstatě přímý vodič.
Rozbor
Nejprve si uvědomíme, že aby se tyč dala do pohybu, musí magnetická síla překonat sílu třecí.
Zjistíme velikost a směr této magnetické síly. Z těchto údajů už jsme schopni určit směr a velikost minimální magnetické indukce, která je potřeba, aby se tyč dala do pohybu.
Řešení
Máme najít nejmenší magnetickou indukci, která dá tyč do pohybu. Zjistíme ji tak, že nejprve určíme nejmenší možnou magnetickou sílu, která na tyč musí působit, aby se dala do pohybu, a z ní indukci vyjádříme.
Promyslíme si, jaké síly na tyč působí.
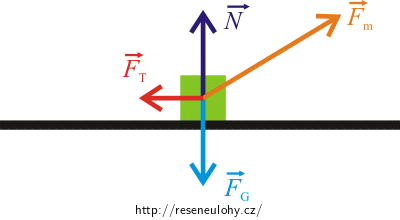
Směrem k Zemi působí gravitační síla \(\vec{F}_\mathrm G\), proti ní působí tlaková síla kolejnic\(\,\vec{N}\), magnetická síla \(\vec{F}_\mathrm m\), která dá tyč do pohybu, a proti směru pohybu působí třecí síla \(\vec{F}_\mathrm T\).
Magnetickou sílu si rozložíme na svislou a vodorovnou složku. (Velikosti sil jsou pouze orientační.)
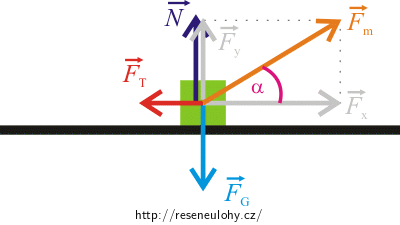
Podrobnější popis tohoto případu naleznete v odstavci úlohy Dívka táhne sáňky po zasněženém chodníku, CELKOVÉ ŘEŠENÍ BODU 2 - velikost tažné síly.
Aby se tyč dala do pohybu, potřebujeme, aby velikost třecí síly FT byla minimálně rovna velikosti vodorovné složky magnetické síly Fx. Jedná se o síly, které působí v jedné přímce, a pro jejich velikosti platí
\[ F_\mathrm T = F_\mathrm x. \]Velikost třecí síly FT spočítáme podle vztahu \[F_\mathrm T=fN,\] kde N je velikost reakční síly kolejnic, kterou díky tomu, že obě síly leží v jedné přímce, spočítáme jako rozdíl velikosti gravitační síly \(F_\mathrm G=mg\) a velikosti svislého průmětu magnetické síly Fy:
\[ F_\mathrm T=f\cdot(mg-F_\mathrm y).\]Nyní dáme oba vztahy dohromady a píšeme
\[f \left(mg-F_\mathrm y\right)=F_\mathrm x.\]Z obrázku výše si vyjádříme oba průměty pomocí velikosti magnetické síly Fm a úhlu α, který magnetická síla svírá s vodorovným směrem. Píšeme
\[f\left(mg - F_\mathrm m \sin{\alpha}\right)=F_\mathrm m \cos{\alpha}. \] Teď už jen vyjádříme Fm: \[ F_\mathrm m=\frac{fmg}{\cos{\alpha}+f\sin{\alpha}}. \]Potřebujeme zjistit, pro jaký úhel je uvedená síla minimální. V čitateli máme konstantu, určíme maximum výrazu ve jmenovateli, a tak zajistíme, že bude daná velikost síly skutečně minimální. Jmenovatele tedy zderivujeme a derivaci položíme rovnu nule.
\[ \frac{\mathrm d(\cos{\alpha}+f\sin{\alpha})}{\mathrm d\alpha}=-\sin{\alpha}+ f\cos{\alpha} \] \[ -\sin{\alpha}+f\cos{\alpha}=0 \] \[ \tan{\alpha}=f \qquad \Rightarrow \qquad \alpha=\arctan{f}, \] \[\alpha=\arctan{f}=\arctan{0{,}6}\,\dot{=}\,31^{\circ}.\]Pozn. Dosazením hodnot větších a menších úhlů, než je námi vypočítaná α, do vztahu pro velikost magnetické síly bychom ověřili, že se jedná skutečně o nejmenší možnou velikost síly.
Toto vyjádření úhlu α dosadíme do vztahu pro velikost magnetické síly Fm, který jsme si spočítali výše, a dostáváme
\[ F_\mathrm m=\frac{fmg}{\cos{\alpha}+f\sin{\alpha}}=\frac{fmg}{\cos{(\arctan{f})}+f\sin{(\arctan{f})}}. \]Použijeme vztah z nápovědy a pro velikost nejmenší magnetické indukce B pak vychází
\[ B=\frac{F_\mathrm m}{Il}=\frac{fmg} {\left[\cos{(\arctan{f})}+f\sin{(\arctan{f})} \right]Il}. \]Směr magnetické indukce je kolmý na směr magnetické síly, tzn. svírá úhel α se svislým směrem. Dále je kolmý na směr rychlosti, která má směr pohybu, a konkrétní směr určíme ze směru proudu.
Zápis a číselné dosazení
m = 0,4 kg hmotnost tyče l = 1 m vzdálenost kolejnic I = 20 A proud protékající tyčí a kolejnicemi f = 0,6 součinitel klidového tření mezi kolejnicí a tyčí B = ? (T) minimální velikost indukce Z tabulek: g = 9,81 m·s−2 tíhové zrychlení
\[ B=\frac{fmg} {\left[\cos{(\arctan{f})}+f\sin{(\arctan{f})} \right]Il}=\frac{0{,}6{\cdot} 0{,}4{\cdot} 9{,}81} {\left[\cos{(\arctan{0{,}6})}+0{,}6\sin{(\arctan{0{,}6})} \right]\cdot 20 {\cdot} 1}\,\mathrm T\,\dot{=}\,0{,}1\,\mathrm T \]Odpověď
Nejmenší magnetická indukce, která dokáže uvést tyč do pohybu, má velikost 0,1 T, je kolmá na magnetickou sílu i na směr pohybu a se svislým směrem svírá úhel 31°. Konkrétní orientaci směru bychom určili podle směru proudu.



