Dívka táhne sáňky po zasněženém chodníku
Úloha číslo: 23
Dívka táhne naložené sáňky o hmotnosti 20 kg po vodorovném zasněženém chodníku. Rychlost saní je konstantní. Koeficient dynamického tření mezi skluznicí a chodníkem je 0,1 a úhel, který svírá provaz s chodníkem, je 30°. Určete:
1) zrychlení sáněk,
2) velikost tažné síly, kterou dívka působí na sáňky,
3) velikost tlakové síly, kterou působí sáňky na chodník,
4) velikost třecí síly působící na sáňky.
Zápis
m = 20 kg hmotnost naložených sáněk fd = 0,1 koeficient dynamického tření mezi skluznicí a chodníkem φ = 30° úhel, který svírá provaz s chodníkem a = ? (m·s-2) zrychlení sáněk T = ? (N) velikost tažné síly, kterou dívka působí na sáňky N = ? (N) velikost tlakové síly, kterou působí sáňky na chodník Ft = ? (N) velikost třecí síly působící na sáňky Nápověda 1 - zrychlení saní, síly působící na sáně
Uvědomte si, co to znamená pro zrychlení (a tedy i výslednou sílu), když je rychlost konstantní. Nakreslete si obrázek a vyznačte v něm všechny síly, které působí na sáňky. Použijte 2. Newtonův zákon \(\mathrm{\Sigma}\vec{F}\,=\,m\vec{a}\) a napište pohybovou rovnici pro sáňky.
Nápověda 2 - pohybová rovnice skalárně
Pohybovou rovnici je třeba zapsat skalárně. Zvolte vhodně souřadný systém, najděte průměty sil do příslušných směrů a přepište v těchto směrech pohybovou rovnici.
Nápověda 3 - velikost tažné síly, třecí síla
Uvědomte si, na čem závisí velikost třecí síly a jak se dá vyjádřit.
Nápověda 4 - velikost tlakové síly
Síla, kterou tlačí sáňky na chodník, je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí chodník na sáňky. Velikost síly N, kterou tlačí chodník na sáně, je již vyjádřena vztahem (5):
\[N \,=\, mg - T\sin\varphi.\tag{5}\]Stačí pouze dosadit.
Nápověda 5 - velikost třecí síly
Velikost třecí síly Ft je již vyjádřena vztahem (4):
\[F_\mathrm{t} \,=\, Nf_\mathrm{d}.\tag{4}\]Stačí pouze dosadit.
CELKOVÉ ŘEŠENÍ BODU 1 - zrychlení saní
Pokud je rychlost sáněk konstantní, jejich rychlost se s časem nemění a zrychlení sáněk je tedy rovno nule (\(\vec{a} \,=\, 0\)).
Odpověď: Zrychlení sáněk a je nulové.
CELKOVÉ ŘEŠENÍ BODU 2 - velikost tažné síly
Síly působící na sáňky:
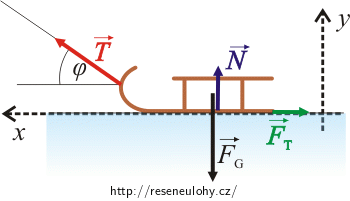
\(\vec{F}_\mathrm{G} \)...síla tíhová
\(\vec{N} \)...síla, kterou tlačí chodník na sáňe
\(\vec{T}\)...hledaná tahová síla, kterou dívka táhne sáňky po chodníku
\(\vec{F}_\mathrm{t}\)...síla třecí, určuje, jak se sáňky „brzdí“ o chodník
Pohybová rovnice pro sáňky:
\[\vec{F}_\mathrm{G}+\vec{N}+\vec{T}+\vec{F}_\mathrm{t}\,=\,m\vec{a}\,=\,0\tag{1}\]m…hmotnost saní
\(\vec{a}\)…zrychlení saní
Protože rychlost \(\vec{v}\) je konstantní, pak je zrychlení \(\vec{a}\) nulové a výslednice sil působících na sáně je tedy také nulová.

Zvolíme vhodně souřadný systém a pohybovou rovnici (1) přepíšeme skalárně. Osu x volíme vodorovně ve směru pohybu a osu y volíme svisle — podle obrázku.
Průmět do osy x:
\[ T\cos\varphi - F_\mathrm{t} \,=\, 0. \tag{2}\]Průmět do osy y:
\[N + T\sin\varphi - F_\mathrm{G} \,=\, 0. \tag{3}\]Třecí síla je úměrná síle, kterou tlačí sáňky na chodník, ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí chodník na sáňky.
Třecí sílu Ft můžeme tedy vyjádřit jako:
\[F_\mathrm{t} = Nf_\mathrm{d}.\tag{4}\]Sílu N, kterou tlačí chodník na sáňky, vyjádříme z rovnice (3):
\[N \,=\, mg - T\sin\varphi.\tag{5}\]Z rovnic (4) a (5):
\[F_\mathrm{t} \,=\, f_\mathrm{d}\left(mg - T\sin\varphi\right).\tag{6}\]Po dosazení rovnice (6) do rovnice (2) můžeme průmět sil do osy x napsat jako:
\[T\cos\varphi - f_\mathrm{d}\left(mg - T\sin\varphi\right) \,=\, 0.\tag{7}\]Z rovnice (7) už jen vyjádříme tahovou sílu:
\[T \,=\, \frac{mgf_\mathrm{d}}{\cos\varphi + f_\mathrm{d}\sin\varphi}.\tag{8}\]Do rovnice (8) dosadíme číselně:
\[T \,=\, \frac{20{\cdot}9{,}81{\cdot}0{,}1}{\cos 30^{\circ} + 0{,}1\cdot\sin30^{\circ}}\,\mathrm{N} \,=\,\frac{19{,}62}{\frac{\sqrt{2}}{2} + 0{,}1{\cdot}0{,}5}\,\mathrm{N},\] \[T\,=\,21{,}4\,\mathrm{N}.\]Odpověď: Velikost tažné síly T, kterou táhne dívka sáňky, je 21,4 N.
CELKOVÉ ŘEŠENÍ BODU 3 - velikost tlakové síly
Síla, kterou tlačí sáňky na chodník, je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí chodník na sáňky. Síla N, kterou tlačí chodník na sáně, je daná vztahem (5):
\[N \,=\, mg - T\sin\varphi.\tag{5}\]Dosadíme-li za T ze vztahu (7), dostaneme výraz:
\[N \,=\, mg - \frac{mgf_\mathrm{d}}{\cos\varphi + f_\mathrm{d}\sin\varphi}\sin\varphi \,=\, mg \left(1 - \frac{f_\mathrm{d}\sin\varphi}{\cos\varphi + f_\mathrm{d}\sin\varphi}\right)\,=\,\] \[\,=\, mg\left(\frac{\cos\varphi}{\cos\varphi + f_\mathrm{d}\sin\varphi}\right) \,=\, mg\left(\frac{1}{1 + f_\mathrm{d}\tan\varphi}\right).\tag{9}\]Dosadíme číselně do rovnice (9):
\[N \,=\, 20{\cdot}9{,}81\left(\frac{1}{1 + 0{,}1\tan30^{\circ}}\right)\,\textrm{N}\,=\, 196{,}2\left(\frac{1}{1 + 0{,}1\frac{\sqrt{3}}{3}}\right)\,\mathrm{N},\] \[N\,=\,185{,}5\,\mathrm{N}.\]Odpověď: Velikost tlakové síly N, kterou působí sáňky na chodník, je 185,5 N.
CELKOVÉ ŘEŠENÍ BODU 4 - velikost třecí síly
Třecí síla Ft je dána vztahem (4):
\[F_\mathrm{t} \,=\, Nf_\mathrm{d}.\tag{4}\]Dosadíme-li do rovnice (4) za N z rovnice (9), pak:
\[F_\mathrm{t} \,=\, mg\left(\frac{1}{1 + f_\mathrm{d}\tan{\varphi}}\right)f_\mathrm{d}.\tag{10}\]Do rovnice (10) dosadíme číselně:
\[F_\mathrm{t}\,=\, 20{\cdot} 9{,}81\left(\frac{1}{1 + 0{,}1\,\tan{30^{\circ}}}\right)0{,}1\,\mathrm{N}\,=\, 19{,}62\,\left(\frac{1}{1 + 0{,}1\frac{\sqrt{3}}{3}}\right)\,\mathrm{N},\] \[F_\mathrm{t}\,=\,18{,}6\,\mathrm{N}.\]Odpověď: Velikost třecí síly Ft působící na sáňky je 18,6 N.
CELKOVÁ ODPOVĚĎ
1) Zrychlení sáněk a je rovno nule.
2) Velikost tažné síly, kterou dívka působí na sáňky, je
\[T \,=\, \frac{mgf_\mathrm{d}}{\cos\varphi + f_\mathrm{d}\sin\varphi}\,=\,21{,}4\,\mathrm{N}.\]
3) Velikost tlakové síly, kterou působí sáňky na chodník, je
\[N \,=\, mg\left(\frac{1}{1 + f_\mathrm{d}\tan\varphi}\right)\,=\,185{,}5\,\mathrm{N}.\]
4) Velikost třecí síly působící na sáňky je
\[F_\mathrm{t} \,=\, mg\left(\frac{1}{1 + f_\mathrm{d}\tan\varphi}\right)f_\mathrm{d}\,=\,18{,}6\,\mathrm{N}.\]







