Setrvačník II
Úloha číslo: 210
Setrvačník o průměru 2 m se rozbíhá z klidu a za čas 20 s dosáhne frekvence 50 otáček za sekundu. Určete jeho úhlovou a obvodovou rychlost na konci rozběhu a počet otočení, které během rozběhu vykoná.
Zápis
D = 2 m průměr setrvačníku tr = 20 s doba rozběhu setrvačníku f0 = 50 Hz frekvence otáčení na konci rozběhu ω = ? úhlová rychlost na konci rozběhu v = ? obvodová rychlost na konci rozběhu i = ? počet otočení během rozběhu Typový příklad
Nápověda 1 – obvodová a úhlová rychlost
Napište si vztah pro výpočet úhlové rychlosti otáčení a vztah mezi touto rychlostí a obvodovou rychlostí.
Nápověda 2 – počet otočení graficky
Nakreslete graf závislosti frekvence otáčení setrvačníku na čase. Kde je v grafu schovaný celkový počet otáček?
Nápověda 3 – počet otočení pomocí integrace
Napište matematicky, jak závisí počet otáček setrvačníku na čase. Jak pomocí této závislosti určíte celkový počet otáček v daném časovém intervalu?
Nápověda 4 – počet otočení úvahou
Rozmyslete si, jak lze celkový počet otáček určit pomocí toho, že se frekvence otáčení mění rovnoměrně.
Celkové řešení
Výpočet úhlové a obvodové rychlosti
Pro úhlovou rychlost platí ω = 2πf.
Na konci rozběhu bude mít setrvačník úhlovou rychlost
\[\omega = 2 \pi f_0 = \left( 2\,\cdot\,\pi\,\cdot\,50\right) \,\mathrm{s^{-1}} \dot{=}\, 314\,\mathrm{s^{-1}}\, . \]Pro obvodovou rychlost platí v = ωr, kde r je vzdálenost otáčejícího se bodu od osy otáčení. Pro bod na okraji setrvačníku je r polovina průměru setrvačníku.
Po dosazení za ω a r dostaneme pro obvodovou rychlost výraz v = πfD.
Obvodová rychlost bodu na okraji setrvačníku na konci rozběhu je
\[v = \pi f_0 D = \left( \pi\,\cdot\, 50\,\cdot\, 2\right) \,\mathrm{m\cdot s^{-1}} \dot{=}\, 314 \,\mathrm{m\cdot s^{-1}}\, .\]Výpočet počtu otočení setrvačníku během rozběhu
a) Grafické řešení
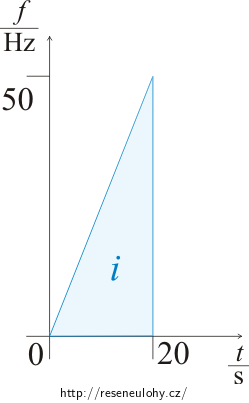
Počtu otáček odpovídá plocha pod křivkou znázorňující závislost frekvence na čase (viz obrázek).
\[i\,=\,\frac{f_{0}t_\mathrm{r}}{2}\]Číselně:
\[i\,=\, \frac{50\,\cdot\,20}{2}\,=\, 500.\]b) Řešení pomocí integrace
Frekvence otáčení se s časem mění podle vztahu:
\(f\left(t\right)\,=\, kt\,,\)kde \(\{k\}\,=\,\frac{50}{20} = \frac{5}{2}\,\)
(směrnice přímky v grafu výše).
Počet otáček setrvačníku od začátku brzdění do zastavení pak můžeme spočítat jako integrál funkce f(t) v daném časovém intervalu (obsah plochy pod křivkou):
\[i\,=\,\int_{0}^{t_\mathrm{r}}{f(t)}\,\mathrm{d}t\,=\, \int_{0}^{t_\mathrm{r}}{(kt)}\,\mathrm{d}t\,,\] \[i\,=\,\left[\frac{kt^{2}}{2}\right]_{0}^{t_\mathrm{r}}\,=\,k\frac{{t_\mathrm{r}}^{2}}{2}\,.\]Číselně:
\[i\,=\, \frac{5}{2}\,\cdot\,\frac{20^{2}}{2}\,=\, 500\,.\]c) Řešení úvahou
Protože frekvence otáčení roste rovnoměrně, můžeme určit průměrnou frekvenci jako aritmetický průměr krajních hodnot. Frekvence vzrostla z nuly na 50 otáček za sekundu. Aritmetický průměr je 25 otáček za sekundu.
Můžeme si představit, že s touto průměrnou frekvencí se setrvačník otáčí po celou dobu rozběhu, tj. 20 s. Celkový počet vykonaných otáček je součin průměrné frekvence a doby rozběhu, tedy 500.
Výsledek
Úhlová rychlost setrvačníku na konci rozběhu je \(\omega = 2\pi f_0 \dot{=}\, 314\,\mathrm{s^{-1}}\,.\)
Jeho obvodová rychlost je \(v = \pi f_0 D \,\dot{=}\, 314 \,\mathrm{m\cdot s^{-1}}\,.\)
Počet otočení, které setrvačník během rozběhu vykoná, je \(i\,=\,\frac{f_{0}t_\mathrm{r}}{2} = 500\).
Podobná úloha
Výpočet počtu otáček si můžete vyzkoušet v úloze Rotor turbíny, podobná metoda výpočtu se využívá i v úloze Snášení letadla.