Zapeklitý padostroj
Úloha číslo: 1231
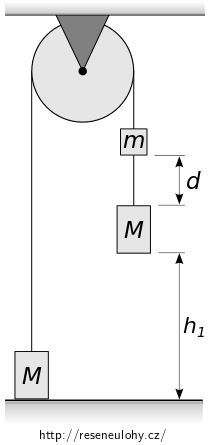
Přes kladku zprvu zajištěnou proti otáčení jsou na tenkém pevném vlákně zavěšena dvě stejná závaží o hmotnostech \(2{,}0~\mathrm{kg}\).
Levé závaží stojí na podlaze, pravé se nachází ve výšce \(1{,}0~\mathrm{m}\) nad podlahou.
Nad pravým závažím ve vzdálenosti \(20~\mathrm{cm}\) je další závaží o hmotnosti \(0{,}5~\mathrm{kg}\).
Vlákno je s výjimkou kladky napnuté ve svislém směru. Kladku v určitém okamžiku uvolníme.
- Jakou rychlostí dopadne pravé dolní závaží na podlahu?
- Do jaké výšky vystoupí levé závaží poté, co pravé dolní závaží dopadne nepružně na podlahu?
- Do jaké maximální výšky pak opět vystoupí pravé dolní závaží?
Hmotnost vlákna i kladky, deformaci vlákna tahem a tření zanedbejte.
Jednotlivé části úlohy řešte nejprve obecně a až následně pro zadané číselné hodnoty.
Průpravná rukojeť před řešením úlohy
K řešení úlohy budeme potřebovat:
- Newtonovy zákony,
- Zákon zachování hybnosti,
- Zákon zachování mechanické energie (není nutný – podle chuti).
Neztratí se nám ani následující dovednosti:
- vědět, jaké síly na těleso působí;
- zapsat pohybovou rovnici pro dané těleso;
- vhodně zavést systém souřadnic a převést vektorové rovnice na skalární;
- řešit jednoduchou soustavu rovnic.
Osvěžme si některé kinematické vztahy:
- Dráha rovnoměrně zrychleného pohybu s nulovou počáteční rychlostí: \[s = \frac{1}{2}at^2\mathrm{.}\]
- Rychlost rovnoměrně zrychleného pohybu s nulovou počáteční rychlostí: \[v = at.\]
Nemáte-li žádné zkušenosti s příklady s kladkou a provázky, zkuste nejprve vyřešit neméně zajímavou úlohu Pevná kladka.
Pozn.: Vektorové veličiny jsou v obrázcích této úlohy značeny tučně.
Zápis
\(M=2{,}0~\mathrm{kg}\) Hmotnost velkého závaží \(m=0{,}5~\mathrm{kg}\) Hmotnost malého závaží \(d=20~\mathrm{cm}\) Vzdálenost závaží na pravé straně \(h_1=1{,}0~\mathrm{m}\) Počáteční výška pravého závaží nad podlahou a) Nápověda 1 – zrychlení soustavy
Naším úkolem je vypočítat rychlost \(v_1\), kterou dopadne pravé dolní závaží na podlahu. Budeme-li znát průběh pohybu závaží, snadno se znalostí \(h_1\) rychlost vypočítáme.
- Jak se bude soustava po uvolnění kladky pohybovat?
- Dokážete určit zrychlení tohoto pohybu?
Pro lepší představu si nakreslete obrázek se všemi silami, které na závaží působí. Vektorově zapište pohybové rovnice. Vhodně zaveďte osu \(y\) a pohybové rovnice přepište do skalárního tvaru. Vypočtěte zrychlení soustavy.
a) Nápověda 2 – dopadová rychlost závaží
Na obrázku máme rozkreslený pohyb závaží od uvolnění kladky (1) přes rovnoměrně zrychlený pohyb soustavy se zrychlením \(a_1\) (2) až po zkoumaný okamžik – dopad pravého dolního závaží na podlahu (3).
Dokážete vypočítat rychlost \(v_1\) pravého dolního závaží při dopadu na podlahu z výšky \(h_1\), víte-li, že se jedná o pohyb s konstantním zrychlením \(a_1\) a počáteční rychlost závaží je nulová?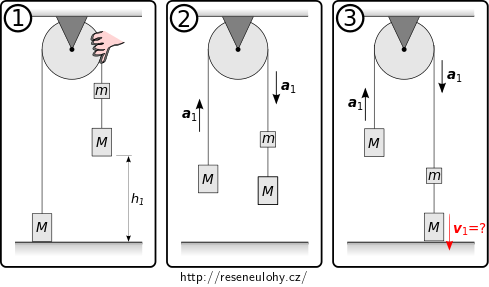
a) Alternativní řešení
Rychlost dopadu pravého dolního závaží na podlahu lze rychleji určit užitím zákona zachování mechanické energie.
Zkoumejme následující stavy soustavy:
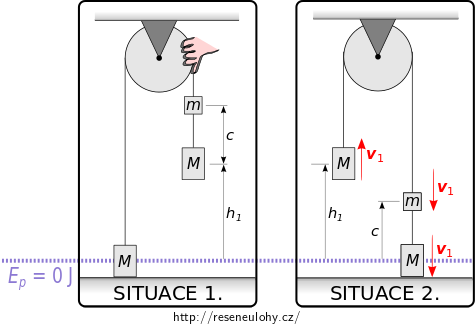
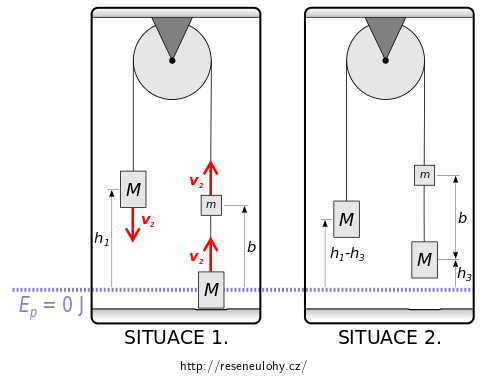
První situace, ve které budeme sledovat celkovou mechanickou energii soustavy, je okamžik těsně před uvolněním soustavy. (SITUACE 1.)
Druhá situace, která je tou nejzazší, při které se původní mechanická energie ještě zachovává, je okamžik bezprostředně před vlastní srážkou pravého spodního závaží s podlahou. (SITUACE 2.)
Zákon zachování mechanické energie:
Energie kladky i vlákna je nulová, neboť jejich hmotnost zanedbáváme. \[ \begin{eqnarray*} E_{\mathrm{situace~1}} & =& E_{\mathrm{situace~2}} \\ Mgh_1 + mg(h_1+c) & =& Mgh_1 + mgc + \frac{1}{2} M v_1^2 + \frac{1}{2} M v_1^2 + \frac{1}{2} m v_1^2\\ mgh_1 &= & \frac{1}{2}(2M+m)v_1^2 \tag{16} \end{eqnarray*} \] Z rovnice (16) vyjádříme hledanou rychlost \(v_1\): \[ v_1 = \sqrt\frac{2mgh_1}{2M+m}. \]b) Nápověda 1 – zrychlení soustavy
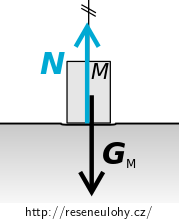
Uvažujte situaci bezprostředně po dopadnutí pravého dolního závaží na podlahu (viz obrázek).
- Jakou rychlost mají jednotlivá závaží bezprostředně po dopadu pravého dolního závaží na podlahu?
- V jakém stavu bude provázek spojující závaží na pravé straně?
- Změní se zrychlení soustavy? Jak?
- Jaký pohyb bude následovat?
Určete velikost a směr zrychlení \(a_2\) soustavy po dopadnutí pravého dolního závaží na podlahu.
b) Nápověda 2 – výška výstupu
Zjistili jsme, že redukovaná soustava, skládající se ze závaží vlevo o hmotnosti \(M\) a vpravo o hmotnosti \(m\), se bude pohybovat nejprve rovnoměrně zpomaleným pohybem se zrychlením \(a_2\). Počáteční rychlost pohybu je \(v_1\).
Dokážete vypočítat dráhu \(s\) tohoto pohybu, kterou urazí závaží do okamžiku zastavení? Jaká bude hledaná výška \(h_2\) levého závaží nad podlahou?
Diskutujte případ, kdy by dráha \(s\gt d\).
b) Alternativní řešení
Výšku \(h_2\), do které vystoupí levé závaží poté, co pravé dolní dopadne nepružně na podlahu, lze určit rychleji užitím zákona zachování mechanické energie.
Při dokonale nepružné srážce pravého spodního závaží s podlahou se mechanická energie soustavy sníží o kinetickou energii příslušící pravému spodnímu závaží bezprostředně před srážkou. Tato část mechanické energie soustavy se přemění ve vnitřní energii dotčených těles.
Po této srážce se celková mechanická energie soustavy sice sníží, ale až do další srážky se tato energie zachovává.
Zkoumejme proto následující stavy soustavy:
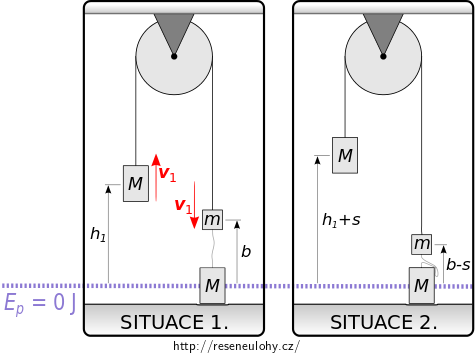
První situace zachycuje okamžik bezprostředně po dokonale nepružné srážce spodního pravého závaží s podlahou. Zbývající závaží se pohybují rychlostí \(v_1\), vypočítanou v části a) této úlohy. (SITUACE 1.)
Druhá situace, ve které budeme sledovat celkovou mechanickou energii soustavy, je okamžik, kdy je rychlost obou závaží na kladce nulová. V tomto okamžiku je totiž výška levého závaží nad podlahou maximální, tj. jedná se o hledanou výšku \(h_2\). (SITUACE 2.)
Zákon zachování mechanické energie:
Energie kladky i vlákna je nulová, neboť jejich hmotnost zanedbáváme. \[ \begin{eqnarray*} E_{\mathrm{situace~1}} & =& E_{\mathrm{situace~2}} \\ Mgh_1 + mgb + \frac12 M v_1^2 + \frac12 m v_1^2 & =& Mg(h_1 + s) + mg(b-s)\\ \frac12 (M+m) v_1^2 &= & (M-m)gs \tag{25} \end{eqnarray*} \] Z rovnice (25) vyjádříme posun soustavy \(s\). Za rychlost \(v_1\) dosadíme z rovnice (15): \[ s = \frac{v_1^2(M+m)}{2g(M-m)} = \frac{h_1 m(M+m)}{(2M+m)(M-m)}. \] Dosadíme číselné veličiny: \[ s = \frac{h_1 m(M+m)}{(2M+m)(M-m)} = \frac{1\cdot\, 0{,}5\cdot(2+0{,}5)}{(2{\cdot} 2 + 0{,}5)(2-0{,}5)}~\mathrm{m} = 0{,}185~\mathrm{m}. \]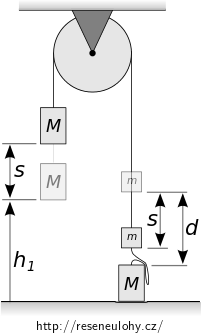
- Aby \(E_\mathrm{k}\) soustavy bylo nulové, musí závaží \(m\) klesnout o \(s=0{,}185~\mathrm{m}\).
- Původní vzdálenost mezi závažími na pravé straně je \(d = 20~\mathrm{cm}\).
Neboť \(s\lt d,\) zastaví se pravé horní závaží nad pravým dolním.
\[h_2 = h_1 + s = (1 + 0{,}185)~\mathrm{m}=1{,}185~\mathrm{m}.\]
Levé závaží vystoupí o \(s\) vzhůru, bude tedy ve výšceV případě, že by \(s\gt d\), došlo by k redukování soustavy pouze na závaží \(M\) na levé straně, které by se pohybovalo rovnoměrně zpomaleně se zrychlením \(g\). Další uražená dráha směrem vzhůru by se dopočítala obdobně.
c) Nápověda 1 – ráz při napnutí lana
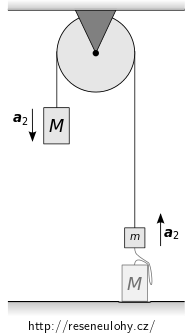
Na obrázku vpravo je zachycena soustava závaží na kladce ve stavu, ve kterém jsme ji ponechali v části b) této úlohy.
Uvědomte si, že soustava na kladce se nezměnila a že výsledné zrychlení soustavy je stále stejné.
- Jak se bude soustava dále pohybovat?
- Co se stane, až se uvolněné lano napne?
- Jakou rychlostí se soustava pohybuje těsně před napnutím lana?
- Jak se změní rychlost soustavy v okamžiku napnutí lana, tj. uvedení ležícího závaží do pohybu?
- S jakým zrychlením se bude soustava pohybovat po napnutí lana? Neznáme jej už?
Vypočtěte rychlost \(v_2\), s jakou se bude soustava pohybovat po napnutí lana, tj. po uvedení ležícího závaží do pohybu.
c) Nápověda 2 – maximální výška
Dokážete vypočítat, na jaké dráze soustava dosáhne nulové rychlosti, pohybuje-li se rovnoměrně zpomaleně se zrychlením \(a_1\) a její počáteční rychlost je \(v_2\)?
Jaká je maximální výška \(h_3\) pravého dolního závaží nad podlahou?
CELKOVÉ ŘEŠENÍ
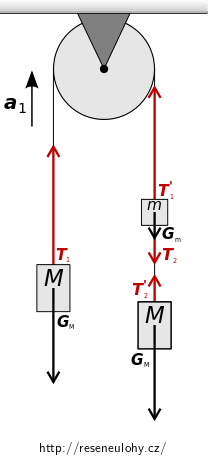
Jaké síly na závaží působí?
Na levé závaží o hmotnosti \(M\) působí:
- tíhová síla \(\vec{G_{\mathrm{M}}},\)
- tahová síla provázku \(\vec{T_{1}}.\)
Na pravé závaží o hmotnosti \(M\) působí:
- tíhová síla \(\vec{G_{\mathrm{M}}},\)
- tahová síla provázku \(\vec{T_{2}^\prime}.\)
Na pravé závaží o hmotnosti \(m\) působí:
- tíhová síla \(\vec{G_{\mathrm{m}}},\)
- tahová síla provázku \(\vec{T_{1}^\prime},\)
- tahová síla provázku \(\vec{T_{2}}.\)
Pohybové rovnice
Všechna závaží se pohybují se stejně velkým zrychlením \(a_1\).
Záváží M vlevo: \[ \vec{G_{\mathrm{M}}} + \vec{T_{1}} = M\vec{a_1}. \tag{1}\] Záváží M vpravo: \[ \vec{G_{\mathrm{M}}} + \vec{T_{2}^\prime} = M\vec{a_1}. \tag{2}\] Záváží m vpravo: \[ \vec{G_{\mathrm{m}}} + \vec{T_{1}^\prime} + \vec{T_{2}} = m\vec{a_1}. \tag{3}\]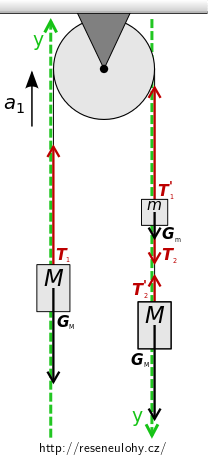
Pohybové rovnice skalárně
Zavedeme vhodně osu \(y\), ve směru předpokládaného zrychlení.Rovnice (1), (2), (3) přepíšeme skalárně:
\[T_{1} - G_{\mathrm{M}} = Ma_1 \qquad\tag{4}\] \[G_{\mathrm{M}} - T_{2}^\prime= Ma_1 \qquad\tag{5}\] \[G_{\mathrm{m}} + T_{2} - T_{1}^\prime= ma_1\qquad\tag{6}\]Akce a reakce, tahové síly
Hmotnost kladky dle zadání zanedbáváme. Kladka tedy nemá žádný moment setrvačnosti a neovlivňuje tahové síly provázku. Závaží M nalevo působí prostřednictvím provázku na závaží m napravo a naopak. Obdobně na sebe působí závaží m a M na pravé straně. Dle 3. Newtonova zákona lze pro velikosti tahových sil psát:
\(T_{1}^\prime = T_{1}, \qquad\)(7)
\(T_{2}^\prime = T_{2}. \qquad\)(8)
Řešení soustavy pohybových rovnic
Sečteme rovnice (4), (5), (6), (7), (8):
\[G_\mathrm{m} = (2M+m)a_1.\tag{9}\]Vyjádříme tíhovou sílu \(G_\mathrm{m}\):
\[G_{\mathrm{m}} = mg. \tag{10}\]Tíhovou sílu z (10) dosadíme do (9):
\[mg = (2M+m)a_1.\tag{11}\]Z (11) vyjádříme hledané zrychlení \(a_1\):
\[a_1 = \frac{mg}{2M+m}.\tag{12}\]Pravé dolní závaží se na počátku nachází ve výšce \(h_1\) nad podlahou a je vůči ní v klidu. Po uvolnění se soustava začne pohybovat se zrychlením \(a_1\). Zkoumané závaží na zem dopadne za čas \(t_1\).
Pro uraženou dráhu za čas \(t_1\) platí:
\[h_1 = \frac{1}{2}a_1 t_1^2.\tag{13}\]Rychlost v čase \(t_1\) je:
\[v_1 = a_1 t_1.\tag{14}\] Z rovnic (13) a (14) vyloučíme čas a vyjádříme hledanou rychlost \(v_1\). Dále za zrychlení \(a_1\) dosadíme výraz (12): \[v_1 = \sqrt{2a_1 h_1} = \sqrt\frac{2mgh_1}{2M+m}.\tag{15}\] Číselným dosazením dostáváme výsledek části a): \[v_1 = \sqrt\frac{2mgh_1}{2M+m} = \sqrt{\frac{2{\cdot} 0{,}5 {\cdot} 9{,}81 {\cdot} 1}{2{\cdot}2 + 0{,}5}}\mathrm{m\cdot s^{-1}} = 1{,}48~\mathrm{m\cdot s^{-1}}.\]
Jak vypadá situace po dopadu závaží?
Bezprostředně po dopadu pravého dolního závaží se bude soustava snažit setrvávat v pohybu rychlostí \(v_1\), kterou jsme vypočítali v části a) této úlohy.
Provázek, kterým jsou závaží na pravé straně spojena, přestane být po dopadu napjat. Tíhová síla \(\vec{G_\mathrm{M}}\) působící na závaží dopadnuté na podlahu bude kompenzována reakcí podložky \(\vec N\), a závaží tak bude setrvávat v klidu.
V souvislosti s uvolněním provázku mezi závažími na pravé straně přestane na závaží o hmotnosti \(m\) působit tahová síla \(\vec{T_2}\). Změní se tak pohybové rovnice, a tedy i zrychlení soustavy.
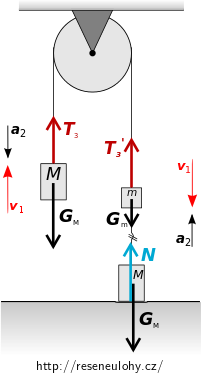
Podle rozložení závaží můžeme soudit, že nové zrychlení \(a_2\) bude mít směr opačný k rychlosti \(v_1\), lze tedy očekávat rovnoměrně zpomalený pohyb s počáteční rychlostí \(v_1\).
Závaží se tedy pohybují zpomaleně v původním směru až do zastavení, pak se směr pohybu otočí a závaží se rozjedou se zrychlením \(a_2\) opačným směrem.
Jaké síly na závaží působí?
Na levé závaží o hmotnosti \(M\) působí:
- tíhová síla \(\vec{G_{\mathrm{M}}},\)
- tahová síla provázku \(\vec{T_{3}}.\)
Na pravé závaží o hmotnosti \(m\) působí:
- tíhová síla \(\vec{G_{\mathrm{m}}},\)
- tahová síla provázku \(\vec{T_{3}^\prime}.\)
Pohybové rovnice
Všechna závaží se pohybují se stejným zrychlením \(a_2\).
Záváží M vlevo: \[ \vec{G_{\mathrm{M}}} + \vec{T_{3}} = M\vec{a_2} \tag{17}\] Záváží m vpravo: \[ \vec{G_{\mathrm{m}}} + \vec{T_{3}^\prime} = m\vec{a_2} \tag{18}\]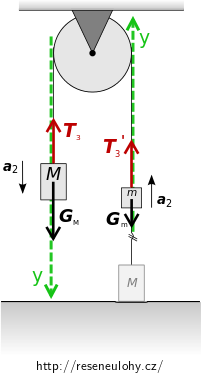
Pohybové rovnice skalárně
Zavedeme vhodně osu \(y\), ve směru předpokládaného zrychlení.Rovnice (17), (18) přepíšeme skalárně:
\(G_{\mathrm{M}} - T_{3} = Ma_2 \qquad\)(19)
\(T_{3}^\prime - G_{\mathrm{m}} = ma_2\qquad\)(20)
Akce a reakce, tahové síly
Hmotnost kladky dle zadání zanedbáváme. Kladka tedy nemá žádný moment setrvačnosti a neovlivňuje tahové síly provázku. Závaží M nalevo působí prostřednictvím provázku na závaží m napravo a naopak. Dle 3. Newtonova zákona lze pro velikosti tahových sil psát:
\(T_{3} = T_{3}^\prime. \qquad\)(21)
Řešení soustavy pohybových rovnic
Sečtením rovnic (19), (20), (21) získáme
\[G_\mathrm{M} - G_\mathrm{m} = a_2(M+m). \] Vyjádříme hledané zrychlení \(a_2\) a dosadíme za tíhové síly: \[ a_2 = \frac{G_\mathrm{M} - G_\mathrm{m}}{M+m} = g\frac{M-m}{M+m}. \tag{22}\]Soustava se bude pohybovat rovnoměrně zpomaleně se zrychlením \(a_2\) do zastavení. Probíha-li děj po dobu \(t_2\), lze počáteční rychlost a dráhu pohybu vyjádřit jako:
\[ v_1 = a_2 t_2, \tag{23}\] \[ s = \frac12 a_2 t_2^2. \tag{24}\] Do rovnice (24) dosadíme za čas \(t_2\) z rovnice (23). Dále dosadíme již vypočítané zrychlení \(a_2\) z rovnice (22) a rychlost \(v_1\) z rovnice (15): \[ s = \frac12 \frac{v_1^2}{a_2} = \frac{h_1 m(M+m)}{(2M+m)(M-m)}. \] Dosadíme číselné veličiny: \[ s = \frac{h_1 m(M+m)}{(2M+m)(M-m)} = \frac{1\cdot\, 0{,}5\cdot(2+0{,}5)}{(2{\cdot} 2 + 0{,}5)(2-0{,}5)}~\mathrm{m} = 0{,}185~\mathrm{m}. \]
- Soustava se bude snažit urazit dráhu \(s=0{,}185~\mathrm{m}\).
- Původní vzdálenost mezi závažími na pravé straně je \(d = 20~\mathrm{cm}\).
Neboť \(s\lt d,\) zastaví se pravé horní závaží nad pravým dolním.
\[h_2 = h_1 + s = (1 + 0{,}185)~\mathrm{m}=1{,}185~\mathrm{m}.\]
Levé závaží vystoupí o \(s\) vzhůru, bude tedy ve výšceV případě, že by \(s\gt d\), došlo by k redukování soustavy pouze na závaží \(M\) na levé straně, které by se pohybovalo rovnoměrně zpomaleně se zrychlením \(g\). Další uražená dráha směrem vzhůru by se dopočítala obdobně.
Lano spojující závaží na pravé straně je stálé volné. Pohybové rovnice uvažované v části b) stále platí a soustava se bude i nádale pohybovat se zrychlením \(a_2\), bude se však jednat o rovnoměrně zrychlený pohyb opačným směrem.
Soustava bude zrychlovat až do okamžiku, kdy se závaží o hmotnosti \(m\) dostane do výšky \(d\) nad spodní pravé závaží.
Celý tento pohyb je opačný k pohybu sledovanému v úloze b). Soustava se tedy bude těsně před napnutím lana pohybovat již známou rychlostí \(v_1\).
Napnutím lana spojujícího závaží na pravé straně se do pohybu uvede závaží dosud ležící na podlaze. Hmotnost soustavy na kladce vzroste na hodnotu \(2M+m\) a rychlost se skokově zmenší na hodnotu \(v_2\). Tento jev můžeme chápat jako analogii dokonale nepružné srážky.
Soustava je po dobu „srážky“ izolovaná a platí zákon zachování hybnosti:
\[\sum_i^N \vec{p_i} = \overset{\longrightarrow}{konst}.\]Celková hybnost soustavy před a po srážce jsou si rovny. \[ \begin{eqnarray} \vec{p_\mathrm{pred}} &= & \vec{p_\mathrm{po}}\\ M\vec{v_1} + m\vec{v_1} &= & M\vec{v_2} + m\vec{v_2} + M\vec{v_2} \end{eqnarray} \] Zavedeme-li osu \(y\) podle obrázku, lze psát zákon zachování hybnosti skalárně: \[ \begin{eqnarray} Mv_1 + mv_1 &= & Mv_2 + mv_2 + Mv_2 \\ v_1(M+m) &= & v_2(2M + m)\\ \end{eqnarray} \] Odtud vyjádříme hledanou velikost rychlosti \(v_2\). Za rychlost \(v_1\) dosadíme z rovnice (15): \[ v_2 = \frac{M+m}{2M+m}v_1 = \frac{M+m}{2M+m}\sqrt{\frac{2mgh_1}{2M+m}}. \tag{26}\]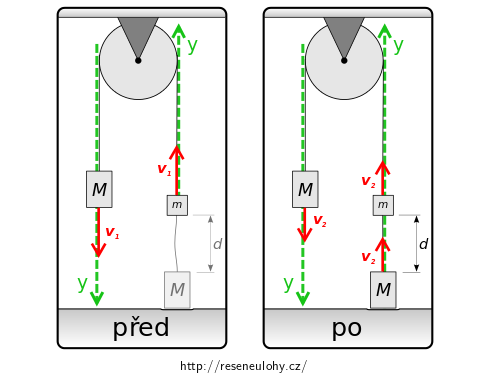
Napnutím lana se závaží dosud ležící na podlaze stalo součástí soustavy, jako tomu bylo na začátku. Soustava se nyní bude opět řídit pohybovými rovnicemi z části a) této úlohy. Následovat tedy bude pohyb rovnoměrně zpomalený s počáteční rychlostí \(v_2\) a zrychlením \(a_1\) vyjádřeným rovnicí (12).
Soustava se bude pohybovat rovnoměrně zpomaleně se zrychlením \(a_1\) do zastavení. Probíhá-li děj po dobu \(t_3\), lze počáteční rychlost a dráhu pohybu vyjádřit jako:
\[ v_2 = a_1 t_3, \tag{27}\] \[ h_3 = \frac12 a_1 t_3^2. \tag{28}\] Do rovnice (28) dosadíme za čas \(t_3\) z rovnice (27). Dále dosadíme již vypočítané zrychlení \(a_1\) z rovnice (12) a rychlost \(v_2\) z rovnice (26): \[ h_3 = \frac12 \frac{v_2^2}{a_1} = h_1\left(\frac{M+m}{2M+m}\right)^2. \] Číselným dosazením získáme hledanou maximální výšku \(h_3\) pravého spodního závaží nad podlahou: \[ h_3 = h_1\left(\frac{M+m}{2M+m}\right)^2 = 1\cdot\left(\frac{2+0{,}5}{2{\cdot} 2 + 0{,}5}\right)^2~\mathrm{m} = 0{,}31~\mathrm{m}. \]CELKOVÁ ODPOVĚĎ
- Pravé dolní závaží dopadne na podlahu rychlostí \(v_1 = 1{,}48~\mathrm{m\cdot s^{-1}}\).
- Poté, co pravé dolní závaží dopadne nepružně na podlahu, vystoupí levé závaží do výšky \(h_2 = 1{,}185~\mathrm{m}\).
- Maximální výška, do které poté pravé dolní závaží vystoupí, je \(h_3 = 0{,}31~\mathrm{m}\).