Moment setrvačnosti válce
Úloha číslo: 555
Určete moment setrvačnosti homogenního válce hmotnosti m a poloměru R:
A) vzhledem k ose procházející středy obou podstav (budeme značit J0),
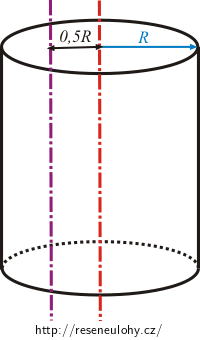
B) vůči ose rovnoběžné se spojnicí středů podstav, ale vzdálené od ní o 0,5R (budeme značit J1).
Bez výpočtu nejprve odhadněte, ve kterém případě bude mít válec větší moment setrvačnosti.
|
|
Komentář k odhadu poměru velikostí J
Moment setrvačnosti závisí na rozložení hmoty tuhého tělesa vzhledem k ose rotace. Není těžké si uvědomit, že tato veličina bude menší pro osu procházející těžištěm tělesa.
Přímým důsledkem Steinerovy věty (viz teorie u úlohy Kutálející se obruč) je tvrzení, že ze všech rovnoběžných os má tuhé těleso nejmenší moment setrvačnosti vůči té, která prochází jeho těžištěm (pouze vůči ní nebude ve vztahu vystupovat Steinerův doplněk).
Rozbor
K výpočtu momentu setrvačnosti válce můžeme vyjít z definičního vztahu \(J = \int_{V} \rho r^2 dV\) a objemový element volit obecně. Výpočet pak vede k trojnému integrálu.
Nechceme-li počítat trojný integrál, můžeme zvolit šikovně objemový element tak, aby byly všechny jeho body stejně vzdálené od osy rotace. Válec „rozřežeme“ na válcové slupky. Moment setrvačnosti jedné slupky snadno vyjádříme. Celkový moment setrvačností pak získáme součtem příspěvků od všech slupek.
Nejjednodušší je ale využít toho, že známe moment setrvačnosti disku (Moment setrvačnosti obruče a disku). Představíme si, že válec „rozřežeme“ na tenké disky. Celkový moment setrvačností pak získáme posčítáním momentů setrvačnosti všech disků.
Postupně si ukážeme všechny možnosti.
Nápověda 1A – řešení úvahou a přes disky
Projděte si teorii a osu řešení u příkladu Moment setrvačnosti tyče. Nebude možné použít některé z řešení úlohy Moment setrvačnosti obruče a disku?
Řešení nápovědy 1A – úvahou a přes disky
Víme-li, že moment setrvačnosti disku hmotnosti md a poloměru R vzhledem k ose procházející jeho středem je \(\frac{1}{2}m_\mathrm{d}R^2\), máme obdobnou otázku týkající se momentu setrvačnosti válce v podstatě vyřešenou.
Moment setrvačnosti tělesa závisí na rozložení hmoty vzhledem k ose otáčení a toto rozložení má homogenní disk a homogenní válec stejné.
Jednoduchou úvahou tedy dojdeme k tomu, že moment setrvačnosti válce vůči ose procházející středy obou podstav je:
\[J_0 = \frac{1}{2}mR^2\,.\]Můžeme si také představit, že válec „rozřežeme“ na tenké disky.
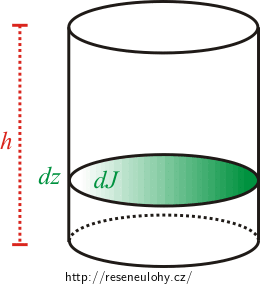
Moment setrvačnosti jednoho disku je:
\[dJ_0 = \frac{1}{2}dmR^2\,.\]kde dm je hmotnost disku:
\[dm = \rho \pi R^2 dz\,,\]ρ je hustota, pro kterou platí:
\[\rho = \frac{m}{V} = \frac{m}{\pi R^2h}\,.\]Pak:
\[dJ_0 = \frac{1}{2}\rho \pi R^4 dz\,.\]Celkový moment setrvačnosti válce získáme posčítáním momentů setrvačnosti všech disků:
\[J_0 = \int dJ_0= \int_{0}^{h} \frac{1}{2}\rho \pi R^4 dz = \frac{1}{2}\rho \pi R^4h\,.\]Dosadíme za hustotu:
\[J = \frac{1}{2}\frac{m}{\pi R^2h}\pi R^4 h= \frac{1}{2} mR^2\,.\]Nápověda 2A – řešení přes slupky
Pokud neznáte moment setrvačnosti disku, můžete si představit, že válec „rozřežete“ na tenké válcové slupky rovnoběžně s osou rotace. Vyjádřete si nejprve moment setrvačnosti jedné slupky a pak posčítejte momenty setrvačnosti všech slupek.
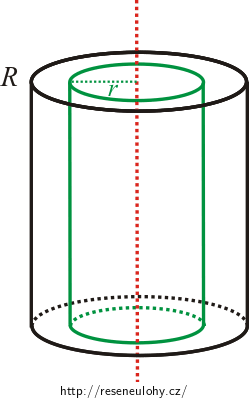
Nápověda 3A – trojný integrál
Můžete vyjít z definice momentu setrvačnosti a objemový element volit obecně. Výpočet pak vede k trojnému integrálu. Vhodné je použít válcové souřadnice.
Řešení nápovědy 3A – trojný integrál
Vyjdeme z definice momentu setrvačnosti tuhého tělesa:
\[J=\int_V \rho r^2 dV\,.\]Válec jednoduše popíšeme v cylindrických (válcových) souřadnicích. Pro přechod \(\vec{r}(x,y,z)\) → \[\vec{r}(r,\varphi,z),\] platí:
\[x=r\cos \varphi\,,\] \[y=r\sin \varphi\,,\] \[z=z\,,\]
kde r náleží <0, R>, φ náleží <0, 2π) a z náleží <0, h>.
Je zřejmé, že objemový integrál můžeme přepsat na trojný. Nesmíme zapomenout na člen, který do integrovaného výrazu přibude kvůli přechodu z kartézských do cylindrických souřadnic.
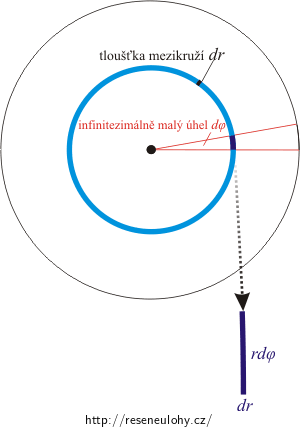
Z obrázku je patrné, že objemový element můžeme vyjádřit jako:
\[dV = r d\varphi dr dz,\] \[J_0 = \int_{0}^{h} \int_{0}^{2\pi} \int_{0}^{R} \rho r^3 dr d\varphi dz = \rho \int_{0}^{h} \int_{0}^{2\pi} \frac{1}{4}R^4 d\varphi dz =\] \[= \rho \int_{0}^{h} 2\pi \frac{1}{4}R^4 dz =\rho h 2\pi \frac{1}{4}R^4\,.\]Upravíme a ve výrazu nalezneme vztah pro výpočet objemu válce:
\[J_0 = \rho h 2\pi \frac{1}{4}R^4 = \frac{1}{2}\rho(\pi R^2 h) R^2 = \frac{1}{2}\rho V R^2\,,\] \[J_0 = \frac{1}{2} m R^2\,.\]Nápověda 1B
Zcela obecné vztahy pro výpočet momentu setrvačnosti tuhého tělesa nejsou příliš jednoduché. Pro speciální případ momentu setrvačnosti homogenního tělesa vůči ose rovnoběžné s osou procházející jeho těžištěm ovšem existuje relativně jednoduchý vzorec známý jako Steinerova věta (viz teorie u úlohy Kutálející se obruč). Použijte tento vzorec pro náš konkrétní případ.
Řešení B
Už známý moment setrvačnosti J0 vůči ose procházející těžištěm válce dosadíme do Steinerovy věty:
\[J_1 = J_0 + md^2 = m(\frac{1}{2}R^2+d^2)\,.\]Kolmou vzdálenost os d máme zadánu. Odtud:
\[J_1 = m(\frac{1}{2}R^2+(\frac{R}{2})^2) = \frac{3}{4}mR^2\,.\]Odpověď
Bez výpočtu je možné určit, že moment setrvačnosti vůči ose procházející těžištěm bude menší než vůči jakékoli ose od těžiště posunuté.
Moment setrvačnosti válce poloměru R a hmotnosti m vůči ose procházející středy obou podstav je:
\[J_0 = \frac{1}{2}mR^2\,.\]Vůči ose rovnoběžné se spojnicí středů podstav vzdálené od ní o 0,5R je moment setrvačnosti roven:
\[J_0 = \frac{3}{4}mR^2\,.\]


