Brzdná síla a auto
Úloha číslo: 196
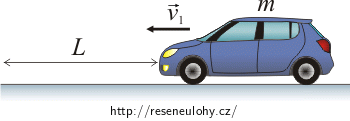
Auto se pohybuje po dráze délky 100 m. Působí na něj brzdná síla velikosti 200 N. Počáteční rychlost auta je 100 km·h−1, hmotnost auta je 1000 kg.
Jaká je rychlost auta na konci dráhy?
Jaké je jeho zrychlení?
Zápis
L = 100 m dráha pohybu auta F = 200 N velikost brzdné síly v1 = 100 km·h−1 počáteční rychlost auta m = 1000 kg hmotnost auta v2 = ? rychlost auta na konci dráhy a = ? zrychlení auta Nápověda 1
K jakým přeměnám energie zde dochází?
Rozmyslete si, kterou fyzikální veličinu je možno vyjádřit jako rozdíl energií.
Nápověda 2: Určení rychlosti
Určete práci vykonanou brzdnou silou a rozdíl kinetických energií na počátku a na konci uvažovaného pohybu.
Jaký vztah mají mezi sebou vykonaná práce a rozdíl energií?
Jak lze ze získaného vztahu určit hledanou rychlost?
Nápověda 3: Zrychlení auta
Rozmyslete si, pomocí kterého fyzikálního zákona můžeme určit zrychlení auta.
Celkové řešení
Asi nejjednodušší bude počítat tuto úlohu přes zákon zachování energie.
Rychlost auta
Při brzdění auta se snižuje jeho rychlost, tedy klesá jeho kinetická energie.
Změna kinetické energie auta je rovna práci vykonané brzdící silou. Ta se projeví zahřátím pneumatik i silnice. Platí:
\[W = \mathrm{\Delta} E_\mathrm{k}.\]Pro práci, vykonanou brzdnou silou, která je konstantní a rovnoběžná se směrem pohybu, platí:
\[W = FL.\]Rozdíl kinetických energií je:
\[\mathrm{\Delta} E_\mathrm{k} = E_\mathrm{k1}-E_\mathrm{k2}=\frac{1}{2}mv_{1}^{2}-\frac{1}{2}mv_{2}^{2}=\frac{1}{2}m\,\left(v_{1}^{2} - v_{2}^{2}\right).\]Z předcházejících rovnic dostáváme:
\[FL = \frac{1}{2}m\,\left(v_{1}^{2} - v_{2}^{2}\right).\]Z této rovnosti vyjádříme hledanou rychlost v2:
\[ \frac{2FL}{m} = v_{1}^{2} - v_{2}^{2}\, \Rightarrow \, v^{2}_{2} = v_{1}^{2}\,-\,\frac{2FL}{m},\] \[v_{2} = \sqrt{v_{1}^{2} - \frac{2FL}{m}}.\]Zrychlení auta
Zrychlení auta vypočítáme z 2. Newtonova zákona:
\[F = ma \, \Rightarrow \, a = \frac{F}{m}.\]Číselné dosazení
Rychlost auta na konci dráhy
\[v_{2} = \sqrt{v_{1}^{2} - \frac{2FL}{m}} = \sqrt{\left(\frac{100}{3{,}6}\right)^{2} - \frac{2{\cdot}200\cdot100}{1000}}\, \mathrm{m \cdot s^{-1}}\dot{=} 27{,}0\, \mathrm{m \cdot s^{-1}}.\]Zrychlení auta:
\[a = \frac{F}{m}= \frac{200}{1000} \,\mathrm{m \cdot s^{-2}}= 0{,}2\,\mathrm{m \cdot s^{-2}}.\]Výsledek
Rychlost auta na konci dráhy:
\[v_{2} = \sqrt{v_{1}^{2} - \frac{2FL}{m}} \dot{=} 27{,}0\, \mathrm{m \cdot s^{-1}} = 97{,}4\, \mathrm{km \cdot h^{-1}}.\]Zrychlení auta:
\[a = \frac{F}{m} \,=\,0{,}2\, \mathrm{m \cdot s^{-2}}.\]Komentář: Alternativní řešení
Rychlost auta na konci dráhy můžeme spočítat i pomocí kinematických vztahů. Určíme nejprve velikost zrychlení auta.
Zrychlení auta vypočítáme z 2. Newtonova zákona:
\[F = ma \, \Rightarrow \, a = \frac{F}{m}.\]Zrychlení auta je konstantní, síla míří proti směru počáteční rychlosti, auto se tedy pohybuje rovnoměrně zpomaleným pohybem. Pro rychlost platí:
\[v_{2} = v_{1} - at.\]Odtud vyjádříme čas brzdění:
\[t = \frac{\left(v_{1} - v_{2}\right)}{a}.\]Pro dráhu rovnoměrně zpomaleného pohybu platí:
\[L\,=\,v_{1}t\,-\,\frac{1}{2}at^{2}.\]Dosadíme za čas t a zrychlení a:
\[L\,=\,\frac{v_{1}\left(v_{1} - v_{2}\right)}{a}\,-\,\frac{1}{2}a \frac{\left(v_{1} - v_{2}\right)^{2}}{a^{2}}\,=\,\] \[\,=\,\frac{1}{2a} \left(2v_{1}^{2} - 2v_{1}v_{2} - v_{1}^{2} + 2v_{1}v_{2} - v_{2}^{2}\right) \,=\,\frac{m}{2F}\left(v_{1}^{2} - v_{2}^{2}\right).\]Odtud:
\[ \frac{2FL}{m} = v_{1}^{2} - v_{2}^{2}\, \Rightarrow \, v^{2}_{2} = v_{1}^{2}\,-\,\frac{2FL}{m},\] \[v_{2} = \sqrt{v_{1}^{2} - \frac{2FL}{m}}.\]



