Pružinové váhy na pólu a na rovníku

Úloha číslo: 201

Pružinové váhy jsme ocejchovali na severním pólu a poté je převezli na rovník.

Budou na rovníku ukazovat stejné údaje jako na pólu? Zdůvodněte.

Nápověda 1 – princip pružinových vah
Na jakém principu pružinové váhy pracují? Jakou fyzikální veličinu vlastně měří?
Řešení k nápovědě 1
Pružinové váhy využívají pro určení hmotnosti závaží elastickou deformaci pružiny. Podle Hookova zákona je relativní prodloužení pružiny přímo úměrné síle, kterou zavěšené závaží na pružinu působí. Této síle říkáme tíha. Pružinové váhy tedy prostřednictvím prodloužení pružiny měří tíhu závaží.
Nápověda 2 – tíha a tíhová síla
Co víte o tíze? Jaký je její vztah k tíhové síle?
Řešení k nápovědě 2
Tíha \(\vec{G}\) (jak jsme už dříve uvedli) je v tomto případě síla, kterou působí zavěšené závaží na pružinu.

Oproti tomu tíhová síla \(\vec{F}_G\) je síla, kterou působí tíhové pole Země na zavěšené závaží.

V daném místě nad zemským povrchem se tyto síly liší pouze působištěm, ale jsou si rovny co do velikosti i směru. Na úlohu lze tedy dále nahlížet tak, že změříme-li pružinovými vahami tíhu, změřili jsme současně i tíhovou sílu.
Nápověda 3 – z čeho je složena tíhová síla
Řekli jsme si, že tíha závaží naměřená pružinovými vahami je rovna tíhové síle, která na závaží působí. Tíhová síla ale vzniká (a její velikost je tedy ovlivněna) složením dvou jiných sil – kterých? Jaký mají tyto síly směr?
Řešení k nápovědě 3
Z hlediska našeho problému je Země neinerciální vztažnou soustavou, která se otáčí kolem své osy s úhlovou rychlostí \(\omega\). Tíhová síla \(\vec{F}_G\) je tedy složením (vektorovým součtem):

a) gravitační síly\(\,\vec{F}_\mathrm{g}\), kterou je závaží přitahováno k Zemi a která míří do středu Země,

b) odstředivé síly\(\,\vec{F}_\mathrm{od}\), která vzniká v důsledku otáčení Země kolem vlastní osy a míří kolmo od osy otáčení (tzv. setrvačná či fiktivní síla, u níž nenajdeme, kdo či co ji působí).

Tedy: \(\vec{F}_\mathrm{G}\,=\,\vec{F}_\mathrm{g}\,+\,\vec{F}_\mathrm{od}.\)
Nápověda 4 – gravitační a odstředivá síla
Už víme, že velikost tíhové síly (a tedy i tíhy měřené pružinovými vahami) závisí na velikosti gravitační síly a odstředivé síly.

Je gravitační síla pro dané závaží všude na povrchu Země stejná? Pokud ne, kde je největší a kde nejmenší?

Je odstředivá síla pro dané závaží všude na povrchu Země stejná? Pokud ne, kde je největší a kde nejmenší?
Řešení k nápovědě 4
Gravitační síla:

Považujeme-li Zemi za kouli, je velikost gravitační síly na jejím povrchu dána Newtonovým gravitačním zákonem:
\[F_\mathrm{g}\,=\,\kappa\frac{mM_\mathrm{z}}{R_\mathrm{z}^2}\,,\]
kde \(\kappa\) je gravitační konstanta, m hmotnost závaží, M_z hmotnost Země a R_z vzdálenost závaží od středu Země – tedy poloměr Země. Velikost této síly je tedy všude na povrchu stejná.

Odstředivá síla:

Každý bod na zemském povrchu se vzhledem k ose otáčení Země pohybuje po kružnici (s výjimkou pólů). Velikost odstředivé síly je dána vztahem:
\[F_\mathrm{od}\,=\,m{\omega^2}r\,=\,m(\frac{2\pi}{T})^{2}r\,,\]
kde m je hmotnost závaží, \(\omega\) úhlová rychlost otáčení, T doba jednoho otočení Země kolem své osy a r poloměr kružnice, po níž bod obíhá vzhledem k ose otáčení. Je zřejmé, že největší je poloměr obíhané kružnice (a tedy i velikost odstředivé síly) pro body na rovníku (zde je to přímo poloměr Země) a s větší zeměpisnou šířkou tento poloměr klesá. Na pólech je pak odstředivá síla nulová.
Nápověda 5
Co z toho vyplývá pro velikost tíhové síly (a tedy i údaje naměřeného pružinovými vahami) na pólu a na rovníku? Kde ukážou pružinové váhy větší hmotnost?
Řešení k nápovědě 5
Na pólu, kde r = 0, je odstředivá síla nulová, tedy platí, že tíhová síla je rovna gravitační co do směru i velikosti:
\[\vec{F}_\mathrm{G(pol)}\,=\,\vec{F}_\mathrm{g},\] \[F_\mathrm{G(pol)}\,=\,F_\mathrm{g}.\] Na rovníku je odstředivá síla maximální a má opačný směr než síla gravitační (viz obrázek): \[\vec{F}_\mathrm{G(rov)}\,=\,\vec{F}_\mathrm{g}\,+\,\vec{F}_\mathrm{od},\] \[F_\mathrm{G(rov)}\,=\,F_{g}\,-\,F_\mathrm{od}.\]
Protože pružinové váhy měří tíhu, jež je stejně velká jako tíhová síla, ukážou tyto váhy na rovníku menší hmotnost než na pólu.
Celkové řešení
Pružinové váhy měří tzv. tíhu − to je síla, kterou působí zavěšené závaží na pružinu. Tíha závaží má stejný směr i velikost jako tíhová síla, kterou na závaží působí Země. Lze se tedy dále zabývat tíhovou silou \(\vec{F}_\mathrm{G}\).

Z hlediska našeho problému je Země neinerciální vztažnou soustavou, která se otáčí kolem své osy s úhlovou rychlostí \(\omega\). Tíhová síla vzniká složením:

1) Gravitační síly \(\vec{F}_\mathrm{g}\) působící mezi Zemí a závažím – tato síla míří do středu Země a její velikost je všude na povrchu Země stejná, daná Newtonovým gravitačním zákonem:
\[F_\mathrm{g}\,=\,\kappa\frac{mM_\mathrm{z}}{R_\mathrm{z}^2}\,,\]
kde \(\kappa\) je gravitační konstanta, m hmotnost závaží, M_z hmotnost Země a R_z vzdálenost závaží od středu Země – tedy poloměr Země.

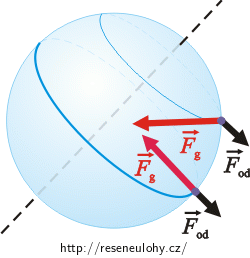
2) Odstředivé síly \(\vec{F}_\mathrm{od}\), která vzniká v důsledku rotace Země kolem své osy (tzv. setrvačná či fiktivní síla, u níž nenajdeme, kdo či co ji způsobuje). Její vektor leží v rovině kolmé na osu otáčení (zemskou osu) a její velikost závisí na místě na povrchu Země. Je vyjádřena vztahem:
\[F_\mathrm{od}\,=\,m{\omega^2}r\,=\,m(\frac{2\pi}{T})^{2}r\,,\]
kde m je hmotnost závaží, \(\omega\) úhlová rychlost otáčení, T doba jednoho otočení Země kolem své osy a r poloměr kružnice, po níž bod obíhá vzhledem k ose otáčení (na rovníku je to poloměr Země).

Platí tedy: \[\vec{F}_\mathrm{G}\,=\,\vec{F}_\mathrm{g}\,+\,\vec{F}_\mathrm{od}.\]

Na pólu, kde r = 0, je odstředivá síla nulová, tedy platí, že tíhová síla je rovna gravitační co do směru i velikosti:
\[\vec{F}_\mathrm{G(pol)}\,=\,\vec{F}_\mathrm{g},\] \[F_\mathrm{G(pol)}\,=\,F_\mathrm{g}.\] Na rovníku je odstředivá síla maximální a má opačný směr než síla gravitační (viz obrázek): \[\vec{F}_\mathrm{G(rov)}\,=\,\vec{F}_\mathrm{g}\,+\,\vec{F}_\mathrm{od},\] \[F_\mathrm{G(rov)}\,=\,F_\mathrm{g}\,-\,F_\mathrm{od}.\]
Protože pružinové váhy měří tíhu, jež je stejně velká jako tíhová síla, ukážou tyto váhy na rovníku menší hmotnost než na pólu.

Pro závaží o hmotnosti 1 kg:
\[M_\mathrm{z}\,=\,5{,}98{\cdot}10^{24}\,\mathrm{kg},\] \[R_\mathrm{z}\,=\,6{,}378{\cdot}10^{6}\,\mathrm{m},\] \[\kappa\,=\,6{,}67{\cdot}10^{-11}\,\mathrm{N\cdot{m^2}\cdot{kg^{-2}}},\] \[T\,=\,24\,\mathrm{h}\,=\,86400\,\mathrm{s},\]
\[F_\mathrm{G(pol)}\,=\,\kappa\frac{mM_\mathrm{z}}{R_\mathrm{z}^2}\,=\,(6{,}67{\cdot}10^{-11}\cdot\frac{1{\cdot}5{,}98{\cdot}10^{24}}{(6{,}378{\cdot}10^6)^2})\,\mathrm{N}\,=\,9{,}805\,\mathrm{N},\]

\[F_\mathrm{G(rov)}\,=\,\kappa\frac{mM_\mathrm{z}}{R_\mathrm{z}^2}\,-\,m(\frac{2\pi}{T})^{2}R_\mathrm{z}\,=\\=\,(6{,}67{\cdot}10^{-11}\cdot\frac{1{\cdot}5{,}98{\cdot}10^{24}}{(6{,}378{\cdot}10^6)^2}\,-\,1\cdot(\frac{2\pi}{86400})^2\cdot{6{,}378{\cdot}10^6})\,\mathrm{N}\,=\,9{,}771\,\mathrm{N}.\]
Výsledek
Pružinové váhy budou pro stejné závaží ukazovat na rovníku nižší hmotnost než na pólu.
Odkaz na podobnou úlohu
Odstředivá síla na rovníku