Malý Pavlík
Úloha číslo: 112
Malý Pavlík se rozjel na kole po přímé cestě. Závislost jeho zrychlení na čase udává následující tabulka:
| t / 10-1s | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a / m·s-2 | 4,0 | 3,7 | 3,3 | 3,0 | 2,6 | 2,3 | 1,9 | 1,6 | 1,2 | 0,8 | 0,4 |
Narýsujte graf a určete tvar funkce a(t). Určete odtud průběh rychlosti a polohy Pavlíka v závislosti na čase.
Předpokládejte, že v čase t = 0 s byl Pavlík v klidu a v počátku soustavy souřadnic.
Poznámka: Přesněji bychom měli mluvit o velikosti zrychlení a velikosti rychlosti. Vzhledem k tomu, že se jedná o přímočarý pohyb a jejich směr se nemění, píšeme jen zrychlení a rychlost.
Nápověda 1: Graf závislosti zrychlení Pavlíka na čase
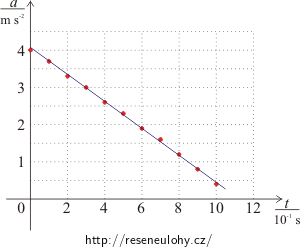
Ze zadané tabulky si nejprve nakreslete graf závislosti zrychlení Pavlíka na čase.
Co je grafem dané závislosti?
Nápověda 2: Vyjádření funkce a(t)
Pro vyjádření funkce a(t) použijte směrnicový tvar přímky.
Nápověda 3: Průběh rychlosti Pavlíka
Víte, jak se s časem mění zrychlení Pavlíka. Jak odtud zjistíte závislost jeho rychlosti na čase?
Nápověda 4: Průběh polohy Pavlíka
Průběh rychlosti Pavlíka již znáte.
Jakým způsobem odvodíte průběh závislosti jeho polohy na čase?
CELKOVÉ ŘEŠENÍ
Poznámka: Rovnice by měly být zapsány ve tvaru např.:
\[y\,=\,1\,\mathrm{m}-2\,\mathrm{m \cdot s^{-1}}\cdot t\,.\]Pro zjednodušení zápisu jednotky ve vztazích nepíšeme.
Podle zadané tabulky nakreslíme graf závislosti zrychlení Pavlíka na čase:
Grafem je přímka.
Pro vyjádření funkce a(t) použijeme směrnicový tvar přímky:
\[a\left(t\right)\,=\,-kt+q\,,\]\(q\, =\, 4\) (průsečík se svislou osou)
\(k\,=\,tg\,\alpha\) (směrnice)
\[tg\alpha\,=\,\frac{\Delta{a}}{\Delta{t}} \,=\, \frac{4-0{,}4}{1} \,=\, 3{,}6\,.\](α je úhel, který přímka svírá s osou x)
Platí: \[a\left(t\right)\,=\,-3{,}6t+4\,.\]Průběh rychlosti získáme integrací vztahu a(t):
\[v\left(t\right)\,=\,\int{a\left(t\right)}dt\,=\,\int{\left(-3{,}6t+4\right)}dt\,,\] \[v\left(t\right)\,=\,-\frac{3{,}6}{2}t^{2}+4t+C\,=\,-1{,}8^{2}+4t+C\,.\]Konstantu C zjistíme z počátečních podmínek:
pro t = 0 s je v = 0 m s-1,
tedy C = 0
Platí:
\[v\left(t\right)\,=\,-1{,}8t^{2}+4t\,.\]Průběh polohy získáme integrací vztahu v(t):
\[s\left(t\right)\,=\,\int{v\left(t\right)}dt\,=\,\int{\left(-1{,}8t^{2}+4t\right)}dt\,,\] \[s\left(t\right)\,=\, -\frac{1{,}8}{3}t^{3}+\frac{4}{2}t^{2}+D \,=\, -0{,}6t^{3}+2t^{2}+D\,.\]Konstantu D zjistíme z počátečních podmínek:
pro t = 0 s je s = 0 m,
tedy D = 0
Platí:
\[s\left(t\right)\,=\,-0{,}6t^{3}+2t^{2}\,.\]Odpověď
Graf závislosti zrychlení Pavlíka na čase:
Vyjádření funkce a(t) je:
\[a\left(t\right)\,=\,-3{,}6t+4\,.\]Průběh rychlosti v(t) je:
\[v\left(t\right)\,=\,-1{,}8t^{2}+4t\,.\]Průběh polohy s(t) je:
\[s\left(t\right)\,=\,-0{,}6t^{3}+2t^{2}\,.\]
