Kladkostroj
Úloha číslo: 100
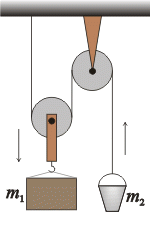
Na soustavě kladek na obrázku je zavěšen kbelík o hmotnosti m2 a kvádr o hmotnosti m1. Určete velikost zrychlení, se kterým se kbelík a kvádr pohybují, a velikost síly T namáhající provaz. Hmotnost kladek a provazu neuvažujte. Kbelík se pohybuje směrem nahoru, kvádr směrem dolů.
Zápis
m1 hmotnost kvádru m2 hmotnost kbelíku a1 = ? velikost zrychlení, se kterým se pohybuje kvádr a2 = ? velikost zrychlení, se kterým se pohybuje kbelík T = ? velikost síly namáhající provaz Nápověda 1 – působící síly a pohybové rovnice
Uvědomte si, jaké síly působí na kbelík a kvádr. Nakreslete si obrázek. Napište pohybové rovnice pro kbelík a pro kvádr.
Nápověda 2 – pohybové rovnice skalárně, provazové síly
Zvolte souřadný systém a pohybové rovnice přepište skalárně. Rozmyslete si, jaké vztahy budou platit pro velikosti provazových sil T, T' a T''.
Nápověda 3 – zrychlení
Rozmyslete si, jaká bude velikost zrychlení a1 vůči a2. Představte si, že kbelík povyjede o vzdálenost s, o jakou vzdálenost klesne kvádr?
Nápověda 4 – velikosti zrychlení, síla T
Dostali jste 2 rovnice (8) a (9) o dvou neznámých T a a1. Vyřešte je a z rovnice (7) dopočítejte velikost zrychlení a2.
CELKOVÉ ŘEŠENÍ
Do obrázku nakreslíme všechny síly působící na kbelík a na kvádr a napíšeme pro ně pohybové rovnice.
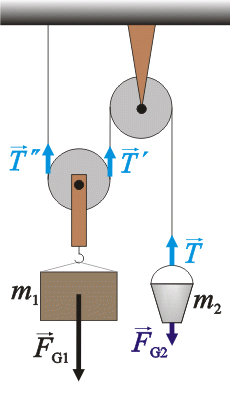
Síly působící na kbelík m2:
\(\vec{F}_\mathrm{G_2}\)…síla tíhová
\(\vec{T}\)…síla, kterou provaz působí na kbelík
Síly působící na kvádr m1:
\(\vec{F}_\mathrm{G_1}\)…síla tíhová
\(\vec{T}^{\prime}\)…síla, kterou provaz působí na kvádr
\(\vec{T}^{\prime\prime}\)…síla, kterou provaz působí na kvádr
Pohybová rovnice pro kbelík:
\[\vec{F}_\mathrm{G_2}+\vec{T}=m_2\vec{a}_2.\tag{1}\]
Pohybová rovnice pro kvádr:
\[\vec{F}_\mathrm{G_1}+\vec{T}^{\prime}+\vec{T}^{\prime\prime}=m_1\vec{a}_1.\tag{2}\]
Zvolme si osu y, jak je vyznačeno na obrázku.
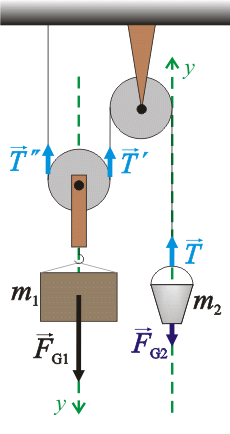
Přepíšeme rovnice (1) a (2) skalárně:
\[T-F_\mathrm{G_2}= m_2a_2,\tag{3}\]
\[F_\mathrm{G_1}-T^{\prime}-T^{\prime\prime} = m_1a_1.\tag{4}\]
Jelikož hmotnost kladek zanedbáváme, nemají žádný moment setrvačnosti a neovlivňují provazové síly. Pro velikosti provazových sil platí:
\[|\vec{T}|=|\vec{T}^{\prime}|=|\vec{T}^{\prime\prime}|.\]
Přepíšeme rovnice (3) a (4):
\[T-F_\mathrm{G_2}= m_2a_2,\tag{5}\]
\[F_\mathrm{G_1}-2T= m_1a_1.\tag{6}\]
Vztah mezi velikostmi zrychlení a1 a a2:
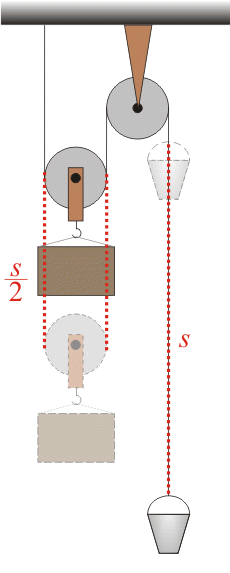
Povyjede-li kbelík o vzdálenost s, poklesne kvádr o vzdálenost \(\frac{s}{2}\):
\[s=\frac{1}{2}a_2t^2,\]
\[\frac{s}{2}=\frac{1}{2}a_1t^2.\]
První rovnici vydělíme druhou rovnicí a dostáváme:
\[2=\frac{a_2}{a_1},\]
\[a_2=2a_1.\tag{7}\]
Rovnice (5) a (6) tedy můžeme přepsat:
\[T-m_2g= m_22a_1,\tag{8}\]
\[m_1g-2T= m_1a_1.\tag{9}\]
Dostáváme dvě rovnice o dvou neznámých, spočteme z nich velikost zrychlení a1 a síly T. První rovnici vynásobíme dvěma a rovnice sečteme:
\[T-m_2g= m_22a_1 \qquad /\cdot2,\]
\[m_1g-2T= m_1a_1.\]
Odtud:
\[m_1g-2m_2g= m_1a_1+4m_2a_1,\]
\[(m_1-2m_2)g= (m_1+4m_2)a_1,\]
\[a_1=\frac{(m_1-2m_2)g}{m_1+4m_2}.\tag{10}\]
Podle vztahu (7) platí:
\[a_2=2a_1=2\frac{(m_1-2m_2)g}{m_1+4m_2}=\frac{(2m_1-4m_2)g}{m_1+4m_2}.\tag{11}\]
Velikost síly T spočteme např. ze vztahu (8):
\[T-m_{2}g= m_22a_1,\] \[T=m_22a_1+m_{2}g=m_2\frac{2(m_1-2m_2)g}{m_1+4m_2}+m_2g,\] \[T=\frac{2(m_2m_1-2m_2^2)g}{m_1+4m_2}+m_2g =\frac{(2m_2m_1-4m_2^2+m_2(m_1+4m_2))g}{m_1+4m_2},\] \[T=\frac{(2m_2m_1-4m_2^2+m_2m_1+4m_2^2)g}{m_1+4m_2}= \frac{3m_2m_1g}{m_1+4m_2},\] \[T=\frac{3m_2m_1g}{m_1+4m_2}.\tag{12}\]CELKOVÁ ODPOVĚĎ
Velikost zrychlení, se kterým se pohybuje závaží, je \[a_1\,=\,\frac{(m_1-2m_2)g}{m_1+4m_2}.\]
Velikost zrychlení, se kterým se pohybuje kbelík, je \[a_2\,=\,2a_1\,=\,\frac{(2m_1-4m_2)g}{m_1+4m_2}.\]
Velikost síly T namáhající provaz je \[T\,=\,\frac{3m_2m_1g}{m_1+4m_2}.\]





