Střela a tyč I
Úloha číslo: 2162
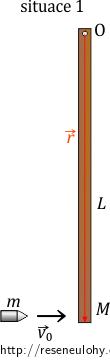
Vodorovně letící střela o hmotnosti \(m\) a rychlosti \(\vec{v_{0}}\) zasáhne dolní konec visící dřevěné tyče délky \(L\) a hmotnosti \(M\) a uvázne v ní. Tyč je volně otáčivá kolem vodorovné osy procházející horním koncem.
a) Určete moment setrvačnosti tyče vzhledem k ose otáčení.
b) Vypočtěte úhlovou rychlost, se kterou se tyč začne otáčet.
c) Vypočtěte poměr změny vnitřní energie soustavy střely a tyče \(\Delta U\) ku počáteční kinetické energii soustavy \(E_\mathrm{k_{0}}\).
Rozbor
Budeme předpokládat, že se střela do tyče po nárazu velmi rychle zaryje a pak se začne tyč se střelou otáčet hledanou úhlovou rychlostí. K řešení úlohy využijeme zákon zachování momentu hybnosti. Vybereme dvě situace: první těsně před nárazem střely do tyče a druhou těsně po nárazu. Zapíšeme si celkový moment hybnosti soustavy střely a tyče v těchto situacích. Z rovnosti velikostí obou momentů hybnosti vyjádříme hledanou úhlovou rychlost.
Při nárazu se střela i tyč zahřívají a deformují, mechanická energie tedy není v tomto případě zachována. Z rozdílu celkové mechanické energie soustavy střely a tyče před nárazem a po něm určíme změnu vnitřní energie soustavy.
Nápověda a)
Předpokládejte, že tyč je homogenní a tenká. Připomeňte si, co nám říká moment setrvačnosti a jak je definován. Rozdělte tyč na menší části (podle délky, hmotnosti) a zapište, jak bude vypadat moment setrvačnosti pro jeden takový kousek tyče.
Nápověda b)
Budeme předpokládat, že se střela po nárazu do tyče rychle zaryje a pak se společně dají do pohybu. K řešení využijeme jeden ze zákonů zachování. Rozmyslete si, která veličina se v dané situaci zachovává.
Nápověda c)
Zapište si, čemu je rovna počáteční mechanická energie soustavy střely a tyče před nárazem střely do tyče a těsně po nárazu. Zamyslete se, zda budou energie stejně velké či ne. Jak vyjádříte změnu vnitřní energie soustavy?
Řešení a)
Představme si homogenní tenkou tyč délky L a hmotnosti M rozsekanou na malé kousky délky \(\Delta\)l a hmotnosti \(\Delta\)M.

Pro moment setrvačnosti jednoho takového kousku \(\Delta J_\mathrm{tyč}\) platí:
\[ \Delta J_\mathrm{tyč} = \Delta M l^2. \tag{1}\]
Tyč považujeme za tenkou a homogenní, hmotnost jednoho kousku \(\Delta\)M tak můžeme vyjádřit pomocí lineární hustoty \(\lambda = \frac{M}{L} \) a jeho délky \(\Delta\)l. Tedy:
\[ \Delta M = \frac{M}{L} \Delta l. \tag{2}\]
Dosadíme z rovnice (2) do rovnice (1). Abychom získali celkový moment setrvačnosti, musíme sečíst příspěvky od všech nekonečně malých kousků, to znamená integrovat. Pro moment setrvačnosti tyče máme:
\[ J_\mathrm{tyč}= \int_0^{L}{\frac{M}{L}l^2}\,\mathrm{d}l. \]
Tyč je zavěšena na jednom svém konci, integrovat budeme přes celou délku tyče, tj. od 0 do L:
Vypočteme integrál:
\[ J_\mathrm{tyč}= \frac{M}{L} \int_0^{L}l^2\,\mathrm{d}l = \frac{M}{L}\left [\frac{l^3}{3} \right ]_0^L = \frac{M}{L}\left [\frac{L^3}{3} \right ]=\frac{ML^2}{3}. \]
Řešení b)
Pro určení úhlové rychlosti využijeme zákon zachování momentu hybnosti. Budeme uvažovat dvě situace, ve kterých se musí celkový moment hybnosti soustavy střela a tyč rovnat. Získáme tak rovnici, ze které úhlovou rychlost vyjádříme.
Moment hybnosti hmotného bodu \(\vec{L}\) vzhledem k bodu O je definován jako vektorový součin polohového vektoru \(\vec r\) a hybnosti \(\vec p\) hmotného bodu:
\[\vec{L} = \vec{r} \times \vec{p}\,.\]Pro velikost vektorového součinu platí
\[L = rp\sin\varphi \,,\]kde φ je úhel sevřený oběma vektory.
Vektor momentu hybnosti je kolmý k rovině určené vektory \(\vec{r}\) a \(\vec{p}\). Jeho orientaci lze určit pravidlem pravé ruky: prsty dáme tak, aby směřovaly od \(\vec{r}\) k \(\vec{p}\), napnutý palec pak ukazuje směr vektoru \(\vec{L}\).
Pro moment hybnosti tuhého tělesa vzhledem k pevné ose otáčení platí
\[\vec{L} = J\vec{\omega}\,,\]kde J je moment setrvačnosti tělesa vzhledem k pevné ose otáčení a \(\vec{\omega}\) je úhlová rychlost otáčení.
Pro velikost momentu hybnosti platí
\[L = J\omega\,.\]Směr vektoru momentu hybnosti je daný směrem vektoru úhlové rychlosti \(\vec{\omega}\).
Moment hybnosti budeme určovat vzhledem k bodu závěsu tyče O.
V první situaci je tyč v klidu, celkový moment hybnosti je tedy roven momentu hybnosti střely. Střela se pohybuje rychlostí v0 kolmo k tyči, vektorový součin můžeme tedy zjednodušit (sinus úhlu mezi vektorem rychlosti a polohovým vektorem je 1). Velikost polohového vektoru \(\vec{r}\) je rovna délce tyče L.
Moment hybnosti pro první situaci je
\[\vec {L_{1}} = \vec {r}×\vec{p}.\]
Vektor momentu hybnosti míří před obrazovku. Pro jeho velikost platí
\[L_{1} = Lp = mv_{0}L.\tag{3}\]
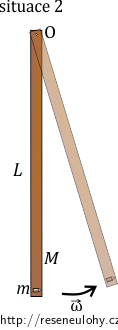
Ve druhé situaci musíme již počítat s otáčivým pohybem tyče kolem osy. Moment setrvačnosti tyče vzhledem k dané ose jsme určili v první části úlohy. V tyči je nyní zaražena střela, musíme tedy ještě přičíst její vliv (střelu považujeme za hmotný bod). Jelikož se střela i tyč pohybují stejnou úhlovou rychlostí, můžeme momenty setrvačnosti tyče Jtyč a střely Jstřela sečíst:
\[ \vec{L_{2}} = \left(J_\mathrm{tyč} + J_\mathrm{střela}\right)\vec{\omega}\,, \]
\[ \vec{L_{2}} = \left(\frac{1}{3}ML^2 + mL^2\right)\vec{\omega}\,. \]
Moment hybnosti míří stejně jako v první situaci před obrazovku. Pro jeho velikost platí
\[ L_{2} = \left(\frac{1}{3}ML^2 + mL^2\right)\omega. \tag{4}\]Ze zákona zachování momentu hybnosti vyplývá rovnost vztahů (3) a (4):
\[ L_{1}=L_{2}, \]
\[ mv_{0}L = \left(\frac{1}{3}ML^2 + mL^2\right)\omega. \]
Vyjádříme úhlovou rychlost \(\omega\):
\[ mv_{0} = \left(\frac{1}{3}M + m\right)L\omega, \]
\[ \omega = \frac{mv_{0}}{\left(\frac{1}{3}M + m\right)L}. \]
Výraz můžeme ještě upravit:
\[ \omega = \frac{3mv_{0}}{\left(M + 3m\right)L}. \]
Řešení c)
Nejprve určíme změnu vnitřní energie soustavy tyče a střely těsně před a těsně po nárazu střely do tyče. Ta je daná rozdílem celkové mechanické energie soustavy před nárazem střely a po něm.
Potenciální energie tyče i střely bude stejná těsně před nárazem a po něm, takže dále se budeme zabývat již jen kinetickou energií. Na počátku má celá soustava jen kinetickou energii střely \(E_\mathrm{k_{0}}\), kinetická energie tyče je nulová, tedy
\[E_\mathrm{k_{0}} = \frac{1}{2}mv_{0}^2.\]Po nárazu střely se dá tyč se zarytou střelou do pohybu úhlovou rychlostí \(\omega\). Vztah pro kinetickou energii rotačního pohybu tělesa vypadá podobně jako v případě kinetické energie translačního pohybu, jen uvažujeme úhlovou rychlost namísto rychlosti a celkový moment setrvačnosti tělesa namísto hmotnosti:
\[E_\mathrm{k} = \frac{1}{2}J_\mathrm{celk} \omega^2.\]Při určování momentu setrvačnosti nesmíme zapomenout, že střela v tyči uvízla a dál se pohybují společně. Momenty setrvačnosti tyče (první část úlohy) a střely (kterou považujeme za hmotný bod) je proto nutné sečíst. Získáváme
\[E_\mathrm{k} = \frac{1}{2}\left(\frac{1}{3}ML^2+mL^2\right)\omega^2.\]Změnu vnitřní energie určíme jako rozdíl počáteční a konečné kinetické energie, tedy:
\[ \Delta U = E_\mathrm{k_{0}} − E_\mathrm{k}. \]
Nyní můžeme vyjádřit hledaný poměr změny vnitřní energie soustavy střely a tyče \(\Delta U\) ku počáteční kinetické energii soustavy \(E_{k_{0}}\) s využitím výše uvedených vztahů:
\[ \frac{\Delta U}{E_\mathrm{k_{0}}} =\frac{E_\mathrm{k_{0}} − E_\mathrm{k}}{E_\mathrm{k_{0}}} =\frac{\frac{1}{2}mv_{0}^2−\frac{1}{2}\left(\frac{1}{3}ML^2+mL^2\right) \omega^2}{\frac{1}{2}mv_{0}^2}. \]
Z druhé části úlohy dosadíme za úhlovou rychlost \(\omega\) a výraz upravíme na
\[ \frac{\Delta U}{E_\mathrm{k_{0}}}=\frac{\frac{1}{2}mv_{0}^2−\frac{1}{6}L^2\left(M+3m\right) \frac{9m^2v_{0}^2}{\left(M + 3m\right)^2L^2}}{\frac{1}{2}mv_{0}^2} = \frac{\frac{1}{2}m−\frac{3}{2} \frac{m^2}{\left(M + 3m\right)}}{\frac{1}{2}m} = 1−\frac{3m}{\left(M + 3m\right)}. \]
Získáváme poměr
\[ \frac{\Delta U}{E_\mathrm{k_{0}}}= \frac{M}{\left(M + 3m\right)}. \]
Odpověď a)
Moment setrvačnosti tyče vzhledem k vodorovné ose otáčení procházející jejím koncem je
\[J_\mathrm{tyč}= \frac{1}{3}ML^2. \]Odpověď b)
Úhlová rychlost, se kterou se začne tyč se střelou otáčet, je \[ \omega = \frac{3mv_{0}}{\left(M + 3m\right)L}. \]
Odpověď c)
Poměr změny vnitřní energie soustavy střely a tyče \(\Delta U\) ku počáteční kinetické energii soustavy \(E_\mathrm{k_{0}}\) je
\[ \frac{\Delta U}{E_\mathrm{k_{0}}} = \frac{M}{\left(M + 3m\right)}. \]
Podobná úloha
Můžete zkusit podobnou úlohu Náraz střely na konec otočné tyče.
Chcete-li zkusit vyřešit o něco těžší úlohu podobného stylu, podívejte se na Střela a tyč II.



