Kubický krystal a hydrostatický tlak
Úloha číslo: 2146
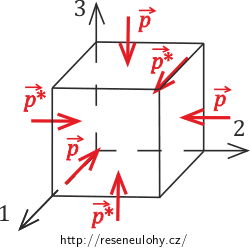
Kubický krystal je podroben hydrostatickému tlaku. Ukažte, v jakém vztahu je stlačitelnost krystalu a modul objemové pružnosti k elastickým konstantám. Krystal uvažujte jako dost malou krychli a tlak berte ve všech třech směrech stejný.
Zápis
sij; i, j = (1; 2; 4) elastické konstanty K = ? (Pa) modul objemové pružnosti γ = ? (Pa−1) stlačitelnost Teorie a značení
V Hookově zákoně pro anizotropní látku používáme soustavu rovnic:
\[\varepsilon_{xx}\,=\,s_{11}\sigma_{xx}+s_{12}\sigma_{yy}+s_{13}\sigma_{zz}+s_{14}\tau_{yz}+s_{15}\tau_{zx}+s_{16}\tau_{xy},\] \[\varepsilon_{yy}\,=\,s_{21}\sigma_{xx}+s_{22}\sigma_{yy}+s_{23}\sigma_{zz}+s_{24}\tau_{yz}+s_{25}\tau_{zx}+s_{26}\tau_{xy},\] \[\varepsilon_{zz}\,=\,s_{31}\sigma_{xx}+s_{32}\sigma_{yy}+s_{33}\sigma_{zz}+s_{34}\tau_{yz}+s_{35}\tau_{zx}+s_{36}\tau_{xy},\] \[\gamma_{yz}\,=\,s_{41}\sigma_{xx}+s_{42}\sigma_{yy}+s_{43}\sigma_{zz}+s_{44}\tau_{yz}+s_{45}\tau_{zx}+s_{46}\tau_{xy},\] \[\gamma_{zx}\,=\,s_{51}\sigma_{xx}+s_{52}\sigma_{yy}+s_{53}\sigma_{zz}+s_{54}\tau_{yz}+s_{55}\tau_{zx}+s_{56}\tau_{xy},\] \[\gamma_{xy}\,=\,s_{61}\sigma_{xx}+s_{62}\sigma_{yy}+s_{63}\sigma_{zz}+s_{64}\tau_{yz}+s_{65}\tau_{zx}+s_{66}\tau_{xy},\]kde
\[\sigma_{xx}, \sigma_{yy}, \sigma_{zz}\]jsou tahová napětí,
\[\tau_{yz}, \tau_{zx}, \tau_{xy}\]jsou smyková napětí,
\[\varepsilon_{xx}, \varepsilon_{yy}, \varepsilon_{zz}\]jsou normálové deformace,
\[\gamma_{yz}, \gamma_{zx}, \gamma_{xy}\]jsou smykové deformace a
\[s_{ij}\]jsou elastické konstanty.
Tenzorem napětí zde rozumíme:
\[\begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \sigma_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \\ \end{bmatrix}.\]Tenzor je symetrický, to znamená, že platí
\[\tau_{yx} = \tau_{xy},\] \[\tau_{zx} = \tau_{xz},\] \[\tau_{zy} = \tau_{yz}.\]Stačí nám tedy uvažovat pouze členy
\[\sigma_{xx}, \sigma_{yy}, \sigma_{zz}, \tau_{yz}, \tau_{zx}, \tau_{xy}.\]Tenzorem deformace je:
\[\begin{bmatrix} \varepsilon_{xx} & \gamma_{xy} & \gamma_{xz} \\ \gamma_{yx} & \varepsilon_{yy} & \gamma_{yz} \\ \gamma_{zx} & \gamma_{zy} & \varepsilon_{zz} \\ \end{bmatrix}.\]I tento tenzor je symetrický, takže
\[\gamma_{yx} = \gamma_{xy}\] \[\gamma_{zx} = \gamma_{xz}\] \[\gamma_{zy} = \gamma_{yz}.\]Máme tedy celkově šest členů pro deformaci
\[\varepsilon_{xx}, \varepsilon_{yy}, \varepsilon_{zz}, \gamma_{yz}, \gamma_{zx}, \gamma_{xy}.\]Soustavu rovnic můžeme uvažovat i inverzně, tedy složky tenzoru napětí lze napsat lineárními vztahy:
\[\sigma_{xx}\,=\,C_{11}\varepsilon_{xx}+C_{12}\varepsilon_{yy}+C_{13}\varepsilon_{zz}+C_{14}\gamma_{yz}+C_{15}\gamma_{zx}+C_{16}\gamma_{xy},\] \[\sigma_{yy}\,=\,C_{21}\varepsilon_{xx}+C_{22}\varepsilon_{yy}+C_{23}\varepsilon_{zz}+C_{24}\gamma_{yz}+C_{25}\gamma_{zx}+C_{26}\gamma_{xy},\] \[\sigma_{zz}\,=\,C_{31}\varepsilon_{xx}+C_{32}\varepsilon_{yy}+C_{33}\varepsilon_{zz}+C_{34}\gamma_{yz}+C_{35}\gamma_{zx}+C_{36}\gamma_{xy},\] \[\tau_{yz}\,=\,C_{41}\varepsilon_{xx}+C_{42}\varepsilon_{yy}+C_{43}\varepsilon_{zz}+C_{44}\gamma_{yz}+C_{45}\gamma_{zx}+C_{46}\gamma_{xy},\] \[\tau_{zx}\,=\,C_{51}\varepsilon_{xx}+C_{52}\varepsilon_{yy}+C_{53}\varepsilon_{zz}+C_{54}\gamma_{yz}+C_{55}\gamma_{zx}+C_{56}\gamma_{xy},\] \[\tau_{xy}\,=\,C_{61}\varepsilon_{xx}+C_{62}\varepsilon_{yy}+C_{63}\varepsilon_{zz}+C_{64}\gamma_{yz}+C_{65}\gamma_{zx}+C_{66}\gamma_{xy},\]kde
\[C_{ij}\]jsou elastické moduly (moduly pružnosti).
Rozbor
Krychle se zde uvažuje dost malá na to, aby se tlak mohl brát ze všech stran konstantní. Není zde žádné smykové působení a jsou zde stejné vlastnosti ve všech třech směrech. Z matice elastických konstant tak dostaneme tři rovnice pro deformace. Pomocí deformací vyjádříme relativní objemovou změnu a z ní pak hledanou stlačitelnost.
Nápověda
Připomeňte si, jak je definovaná stlačitelnost a čemu je roven modul objemové pružnosti.
Vyjádřete si přechod od napětí k deformacím pomocí příslušné matice elastických konstant. Neuvažujte zde rovnice pro úhlové deformace. Ve všech třech směrech budou podmínky stejné, takže všechna tři tahová napětí lze označit stejným tlakem, a budou zde hrát roli pouze dvě elastické konstanty. Získáte tři rovnice pro deformace. Použijte dále vztah mezi deformacemi a relativní objemovou změnou. Pak už lze vyjádřit stlačitelnost a v převrácené hodnotě i modul objemové pružnosti.
Řešení
Stlačitelnost je daná vztahem:
\[\gamma\,=\,-\frac{1}{V_0}\frac{\Delta V}{\Delta p}.\tag{1}\]Pro modul objemové pružnosti platí:
\[K\,=\,\frac{1}{\gamma}.\tag{2}\]Ze symetrie krystalu plyne, že zde stačí uvažovat pouze tři elastické konstanty:
\[s_{11}, s_{12}, s_{44}.\]Poznámka: Jako matici přechodu od složek tenzoru napětí do složek tenzoru deformace můžeme pro kubický krystal uvažovat:
\[\begin{pmatrix} s_{11} & s_{12} & s_{12} & 0 & 0 & 0 \\ s_{12} & s_{11} & s_{12} & 0 & 0 & 0 \\ s_{12} & s_{12} & s_{11} & 0 & 0 & 0 \\ 0 & 0 & 0 & s_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & s_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & s_{44} \end{pmatrix}.\]Hookův zákon pro kubický krystal má tedy tvar:
\[\varepsilon_{xx}\,=\,s_{11}\sigma_{xx}+s_{12}\sigma_{yy}+s_{12}\sigma_{zz},\tag{3}\] \[\varepsilon_{yy}\,=\,s_{12}\sigma_{xx}+s_{11}\sigma_{yy}+s_{12}\sigma_{zz},\tag{4}\] \[\varepsilon_{zz}\,=\,s_{12}\sigma_{xx}+s_{12}\sigma_{yy}+s_{11}\sigma_{zz},\tag{5}\] \[\gamma_{yz}\,=\,s_{44}\tau_{yz},\tag{6}\] \[\gamma_{zx}\,=\,s_{44}\tau_{zx},\tag{7}\] \[\gamma_{xy}\,=\,s_{44}\tau_{xy}.\tag{8}\]Tečná napětí jsou nulová:
\[\tau_{yz}\,=\,\tau_{zx}\,=\,\tau_{xy}\,=\,0.\]Krychli uvažujeme dost malou na to, abychom napětí působící na stěny kubického krystalu mohli brát za konstantní. Také zde uvažujme, že napětí je ve všech třech směrech stejné. Složky napětí v prvních třech rovnicích pak můžeme označit jako tlak p. Musíme ještě uvažovat záporné znaménko, jelikož jde o tlak, nikoliv tah.
Pak:
\[\sigma_{xx}\,=\,\sigma_{yy}\,=\,\sigma_{zz}\,=\,-p\]Z (3), (4), (5) dostáváme:
\[\varepsilon_{xx}\,=\,-p\left({s_{11}+2s_{12}}\right),\tag{9}\] \[\varepsilon_{yy}\,=\,-p\left({s_{11}+2s_{12}}\right),\tag{10}\] \[\varepsilon_{zz}\,=\,-p\left({s_{11}+2s_{12}}\right).\tag{11}\]Pro objemovou deformaci při počátečním objemu V0 platí:
\[\frac{\Delta V}{V_0}\,=\,\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}.\tag{12}\]Pravou stranu vztahu (12) můžeme získat sečtením rovnic (9), (10) a (11), takže získáme rovnici:
\[\frac{\Delta V}{V_0}\,=\,-3p\left({s_{11}+2s_{12}}\right).\tag{13}\]Tlak p je v podstatě tou změnou, kterou jsme potřebovali pro změnu původního objemu. Takže ještě můžeme (13) trochu upravit na:
\[\frac{\Delta V}{V_0}\,=\,-3\Delta p\left({s_{11}+2s_{12}}\right).\tag{14}\]Pro stlačitelnost pak podle (1) dostáváme:
\[\gamma\,=\,-\frac{1}{V_0}\frac{\Delta V}{\Delta p}\,=\,3\left({s_{11}+2s_{12}}\right).\tag{15}\]Modul objemové pružnosti K je jen převrácenou hodnotou stlačitelnosti γ, pak tedy:
\[K\,=\,\frac{1}{3\left({s_{11}+2s_{12}}\right)}.\]Poznámka: Kdybychom chtěli K vyjádřit pomocí elastických modulů C, pak platí:
\[C_{11}+2C_{12}\,=\,\frac{1}{\left({s_{11}+2s_{12}}\right)},\]a tedy
\[K\,=\,\frac{1}{3} {\left(C_{11}+2C_{12}\right)}.\]Odpověď
Stlačitelnost kubického krystalu při působení hydrostatického tlaku vzhledem k elastickým konstantám je:
\[\gamma\,=\,3\left({s_{11}+2s_{12}}\right).\]Pro modul objemové pružnosti platí:
\[K\,=\,\frac{1}{3\left({s_{11}+2s_{12}}\right)}.\]


