Klouzání úsečky I
Úloha číslo: 186
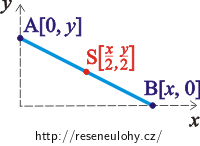
Úsečka AB konstantní délky l se pohybuje tak, že její koncové body kloužou po y-ové, resp. x-ové ose pravoúhlé soustavy souřadnic. (Obrázek ukazuje situaci v 1. kvadrantu.)
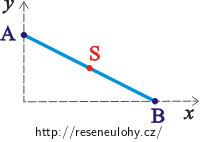
Zjistěte, jakou trajektorii bude při tomto pohybu opisovat střed S uvedené úsečky.
Nápověda 1
Napište si souřadnice bodů A, B. Souvisejí tyto souřadnice nějak s délkou l úsečky AB?
Nápověda 2
Napište si souřadnice bodu S. Pohyb tohoto bodu budeme sledovat – zkuste tedy pomocí jeho souřadnic vyjádřit souřadnice bodů A a B.
Nápověda 3
Sledujeme pohyb středu S, proto chceme „dostat“ do vztahu (1) jeho souřadnice. Dosaďte tedy za x, y výrazy s xs a ys a výraz upravte.
Jakou křivku popisuje výsledný vztah?
Celkové řešení
Vyjádříme souřadnice bodů A, B:
A=[0;y],
B=[x;0].
Označíme souřadnice středu úsečky: \(S = [x_\mathrm{s};y_\mathrm{s}]\) a vyjádříme \(S = [x_\mathrm{s};y_\mathrm{s}]=[\frac{x}{2};\frac{y}{2}].\)
Odtud lze určit x a y:
\[x_\mathrm{s}=\frac{x}{2}\Rightarrow x = 2x_\mathrm{s},\]
\[y_\mathrm{s}=\frac{y}{2}\Rightarrow y = 2y_\mathrm{s}.\]
Délku úsečky můžeme vyjádřit pomocí Pythagorovy věty a za x, y dosadit:
\[l^{2}=x^{2}+y^{2}=((2x_\mathrm{s})^{2}+(2y_\mathrm{s})^{2})=4(x_\mathrm{s}^{2}+y_\mathrm{s}^{2})\,.\]
Úpravou dostáváme:
\[(\frac{l}{2})^{2}=x_\mathrm{s}^{2}+y_\mathrm{s}^{2}\,,\]
což je rovnice kružnice.
Trajektorií bodu S je tedy kružnice. (Pokud necháme body A a B procházet pouze částí souřadnicových os ohraničující 1.kvadrant, jak ukazuje obrázek, bude se jednat o čtvrtinu kružnice.)
Poznámky:1) Na tomto principu je založena proužková metoda konstrukce kružnice: Nakreslete si na papír dvě navzájem kolmé přímky. Vezměte si proužek papíru (jeho délka je průměrem budoucí kružnice) a vyznačte na něm jeho střed. Položte proužek na papír tak, aby krajní body ležely každý na jiné přímce. V místě středu proužku vyznačte na papír bod kružnice. Posouváním krajních bodů proužku po přímkách vám začne střed proužku vykreslovat kružnici.
2) Pokud místo dvou kolmých přímek na začátku narýsujete dvě různoběžné přímky, získáte uvedeným postupem elipsu. Elipsu tímto postupem získáte také v případě, že přímky budou kolmé, ale místo středu proužku budete při konstrukci využívat jeho jiný libovolný bod (viz úloha Klouzání úsečky II).
Výsledek
Trajektorií středu úsečky je kružnice.
Vizualizace pomocí apletu
Kliknutím na tlačítko „Zapnout animaci“ se spustí animace klouzání úsečky po souřadnicových osách, opětovné kliknutí animaci zastaví. Čas \(t\) je možné měnit na posuvníku. Tlačítko „Zapnout stopu“ zapíná/vypíná stopu bodu S. Po zaškrtnutí tlačítka „Zobrazit trajektorii“ se zobrazí trajektorie bodu S bez nutnosti vykreslení stopou bodu S. Tlačítko „Reset“ zastaví animaci a vrátí aplet do původního stavu.
Z apletu je dobře vidět, že bod S opisuje kružnici se středem v počátku souřadnic.