Hráz přehradní nádrže z hlediska mechaniky
Úloha číslo: 1152
Hladina vody dosahuje u hráze přehrady výšky h (viz obrázek hráze z boku), hráz má délku l. Určete:
- Velikost výsledné síly F, která se snaží odsunout hráz ve vodorovném směru.
- Velikost výsledného momentu síly M, který se snaží hráz otočit kolem bodu O.
- Výšku nad patou hráze H, ve které by výše určená síla F měla moment M.
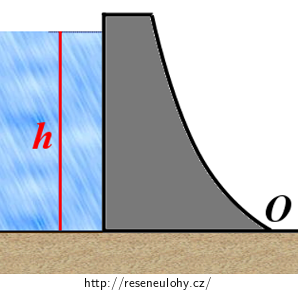
Rozbor
Intuitivně tušíme, že síla snažící se hráz odsunout ve vodorovném směru bude v různé hloubce pod hladinou různá. Musíme se tedy zaměřit nejdříve na zkoumání konkrétní, velmi malé části hráze v konkrétní hloubce. Proto v hloubce y pod hladinou vody vyznačte v tělese hráze vodorovný pruh o výšce dy, který budeme považovat za infinitezimálně tenký. Tím vznikne na vnější i vnitřní straně hráze plošný element dS, pro který zjevně platí:
\[dS\,=\,ldy,\tag{1}\]kde l je délka hráze. (Protože tloušťka dy je infinitezimálně malá, můžeme si dovolit považovat vnitřní i vnější plošný element za shodné obdélníky.) Geometrii úlohy ukazují obrázky níže.
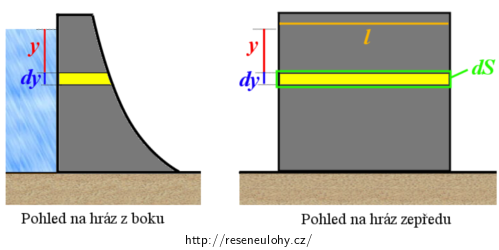
Nyní budeme dále zkoumat, jaké tlakové síly působí ve vodorovném směru na tyto dva vzniklé plošné elementy.
Nápověda 1 (k části a.)
Jaký tlak působí na plošku o obsahu dS na vnitřní straně hráze (tj. té, která je zalita vodou)? Určete tlakovou sílu na uvedenou plošku. Analogicky postupujte v případě vnější stěny hráze.
Nápověda 2 (k části a.)
Síly získané v předcházejícím kroku zakreslete do obrázku. Jaká výsledná síla dF bude na plošný element dS působit?
Nápověda 3 (k části a.)
Hydrostatický tlak ph působící na plošku dS vyjádřete jako funkci hloubky y a za dS dosaďte ze vztahu (1). Tím je úprava výrazu dF u konce. Jak z této infinitezimální síly určíme celkovou sílu F působící na stěnu hráze?
Nápověda 4 (k části b.)
V případě momentu síly postupujte obdobně. Vyjádřete si nejprve infinitezimální moment dM síly dF vzhledem k bodu O jako funkci hloubky y.
Nápověda 5 (k části b.)
Integrálem přejděte od infinitezimálního výrazu dM k celkovému momentu M.
Nápověda 6 (k části c.)
Známe nyní výslednou sílu a její výsledný moment. Jak zjistíme výšku H, ve které by síla F musela bodově působit, aby byl její moment roven M? Uvědomte si, jaký je vztah mezi hledanou výškou H a ramenem, které by měla síla F.
Celkové řešení
Část a.
Intuitivně tušíme, že síla snažící se hráz odsunout ve vodorovném směru bude v různé hloubce pod hladinou různá. Musíme se tedy zaměřit nejdříve na zkoumání konkrétní, velmi malé části hráze v konkrétní hloubce. Proto v hloubce y pod hladinou vody vyznačte v tělese hráze vodorovný pruh o výšce dy, který budeme považovat za infinitezimálně tenký. Tím vznikne na vnější i vnitřní straně hráze plošný element dS, pro který zjevně platí:
\[dS\,=\,ldy,\tag{1}\]kde l je délka hráze. (Protože tloušťka dy je infinitezimálně malá, můžeme si dovolit považovat vnitřní i vnější plošný element za shodné obdélníky.) Geometrii úlohy ukazují obrázky níže.

Nyní budeme dále zkoumat, jaké tlakové síly působí ve vodorovném směru na tyto dva vzniklé plošné elementy.
Na vnitřní straně hráze působí na plošku dS hydrostatický tlak ph, vyvolaný tíhou vodního sloupce nad ploškou, a atmosférický tlak pa. Celkový tlak na plošku je tedy:
\[p\,=\,p_\mathrm{h}\,+\,p_\mathrm{a}.\tag{2}\]Pro velikost infinitezimální tlakové síly dF1 na plošku platí:
\[dF_1\,=\,pdS\,=\,p_\mathrm{h}dS\,+\,p_\mathrm{a}dS.\tag{3}\]Na vnější straně hráze působí na plošku dS pouze atmosférický tlak pa, pro velikost infinitezimální tlakové síly dF2 tedy platí:
\[dF_2\,=\,p_\mathrm{a}dS.\tag{4}\]Poznámka: Atmosférický tlak jsme uvažovali na obou stranách hráze stejný, což představuje určité zanedbání. Kdybychom chtěli být zcela precizní, měli bychom započítat skutečnost, že na vnější straně hráze je vzduchový sloupec o výšku y mohutnější, a tudíž je zde atmosférický tlak větší. Nicméně vzhledem k tomu, že se atmosférický tlak v závislosti na počasí běžně mění v řádu minut až o stovky pascalů, můžeme si naše zjednodušení dovolit.
Dopočtené síly dF1 a dF2 znázorníme v obrázku (níže).
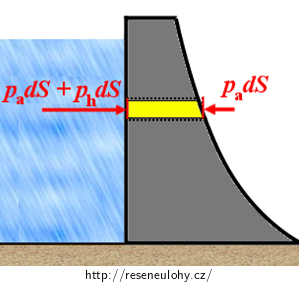
Z obrázku je patrné, že stejně velké atmosférické tlakové síly působí proti sobě a jejich účinky se vyruší. Výsledná infinitezimální síla dF působící na plošku dS má tedy velikost:
\[dF\,=\,dF_1\,-\,dF_2\,=\,p_\mathrm{h}dS.\tag{5}\]Pro hydrostatický tlak jako funkci hloubky platí známý vztah:
\[p_\mathrm{h}(y)\,=\,{\varrho}gy,\tag{6}\]kde ρ je hustota vody a g tíhové zrychlení. Protože ploška dS je infinitezimálně tenká, můžeme považovat hydrostatický tlak na ni působící za konstantní. Dosazením ze vztahů (1) a (6) do rovnice (5) dostáváme:
\[dF\,=\,p_\mathrm{h}dS\,=\,{\varrho}gyldy.\tag{7}\]Je vidět, že velikost síly F se mění s hloubkou, F = F(y). Chceme-li nyní určit výslednou sílu F, vyintegrujeme element dF přes y od 0 do h:
\[F\,=\,\int{dF}\,=\,{\varrho}gl\int_0^h{ydy}\,=\,{\varrho}gl[\frac{1}{2}y^2]_0^h\,=\,\frac{1}{2}{\varrho}glh^2.\tag{8}\]Část b.
Opět budeme pracovat nejdříve s infinitezimálními veličinami. Pro velikost infinitezimálního momentu dM platí:
\[dM\,=\,rdF,\tag{9}\]kde r je rameno síly dF. Toto rameno je maximální u hladiny a nulové u dna nádrže. Z dřívějších obrázků je vidět, že platí:
\[r\,=\,h\,-\,y.\tag{10}\]Dosazením vztahů (7) a (10) do výrazu (9) dostáváme:
\[dM\,=\,(h\,-\,y){\varrho}gyldy. \tag{11}\]Integrací výrazu dM přes všechna y od 0 do h dostáváme:
\[M\,=\,\int{dM}\,=\,{\varrho}gl\int_0^h{y(h-y)dy}\,=\,{\varrho}gl [\frac{hy^2}{2}-\frac{y^3}{3}]_0^h\,=\,\frac{{\varrho}glh^3}{6}.\tag{12}\]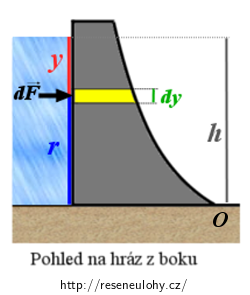
Část c.
Z dřívějších obrázků je patrné, že hledaná výška H by byla přímo ramenem síly F. Platí tedy:
\[M\,=\,HF\,\Rightarrow\,H\,=\,\frac{M}{F}.\tag{13}\]Po dosazení ze vztahů (8) a (12) do rovnice (13) dostáváme:
\[H\,=\,\frac{\frac{1}{6}{\varrho}glh^3}{\frac{1}{2}{\varrho}glh^2}\,=\,\frac{h}{3}.\tag{14}\]Odpověď
Část a: Pro velikost celkové síly F, kterou se voda snaží odsunout hráz ve vodorovném směru, platí:
\[F\,=\,\frac{1}{2}{\varrho}glh^2.\]Část b: Pro velikost celkového momentu síly M, kterou se voda snaží otočit hráz kolem bodu O, platí:
\[M\,=\,\frac{1}{6}{\varrho}glh^3.\]Část c: Kdybychom sílu F umístili do jednoho bodu, muselo by to být ve výšce h/3 nade dnem přehrady, aby měla síla F moment M.


