Pohyb daný graficky I
Úloha číslo: 15
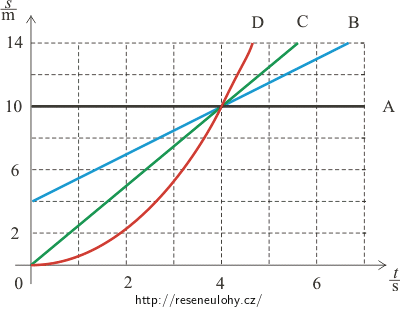
Na obrázku jsou grafy závislosti dráhy na čase přímočarých pohybů autíček A, B, C, D.
a) Charakterizujte slovy pohyb jednotlivých autíček.
b) Určete průměrnou velikost rychlosti jednotlivých autíček v časovém intervalu od 0 s do 4 s.
c) Určete velikost okamžité rychlosti jednotlivých autíček v čase 4 s.
d) Sestrojte do jednoho obrázku grafy závislosti rychlosti na čase pro jednotlivá autíčka.
e) Určete celkově uraženou dráhu v čase t1 = 10 s jednotlivých autíček (včetně případné počáteční nenulové dráhy), pokud by pohyb pokračoval podle uvedené grafické závislosti.
Nápověda 1 pro a): Popisy pohybů
Graf A: Mění se dráha s časem?
Graf B, C: Jaká matematická funkce popisuje závislost dráhy na čase těchto pohybů? Co můžete říct o přírůstku dráhy za stejné časové intervaly u těchto pohybů a co o rychlosti?
Graf D: Jaká matematická funkce popisuje závislost dráhy na čase u tohoto pohybu? Jak se bude měnit s časem rychlost tohoto pohybu?
Nápověda 2 pro b): Uražená dráha, průměrná rychlost
Jakou dráhu urazila autíčka v časovém intervalu od 0 s do 4 s?
Jak spočítáte průměrnou velikost rychlosti, znáte-li dráhu a čas?
Nápověda 3 pro c): Okamžitá rychlost
Graf A, B, C: Jak se s časem mění rychlost u těchto pohybů?
Kde je v grafech s(t) „schovaná“ rychlost?
Graf D: Jak se s časem mění dráha rovnoměrně zrychleného pohybu?
Umíte s využitím hodnot z grafu spočítat zrychlení? Co pak platí pro okamžitou rychlost?
Nápověda 4 pro d): Grafy v = v (t)
Z odpovědí na předchozí nápovědy víte, jak se s časem mění rychlost u jednotlivých pohybů, a znáte i její velikost v určitém čase. Stačí to jen zakreslit do grafu.
Nápověda 5 pro e): Uražená dráha
Vyjádřete matematicky závislosti dráhy na čase s(t) dané grafem. (Pro graf D najdete odpověď v řešení bodu c)).
Pak zjistěte hodnotu dráhy pro t = t1 = 10 s.
CELKOVÉ ŘEŠENÍ
a) Graf A: Dráha autíčka A se s časem nemění. Autíčko je v klidu. Počáteční uražená dráha je 10 m.
Graf B: Jedná se o lineární závislost dráhy na čase. Rychlost pohybu se nemění. Jde o rovnoměrný přímočarý pohyb s počáteční uraženou dráhou 4 m.
Graf C: Jedná se o lineární závislost dráhy na čase. Rychlost pohybu se nemění. Jde o rovnoměrný přímočarý pohyb s nulovou počáteční uraženou dráhou.
Graf D: Grafem dráhy je parabola – dráha narůstá kvadraticky s časem. Rychlost pak roste lineárně s časem. Jedná se o rovnoměrně zrychlený přímočarý pohyb s nulovou počáteční dráhou.
b) Průměrná velikost rychlosti vp je určena podílem uražené dráhy a odpovídajícího časového intervalu, tedy 4 s:
A: uražená dráha \(s_4 =\, 0\), \(v_\mathrm{p}=\,0\),
B: uražená dráha \(s_4 =\, 6 \,\mathrm{m}\), \(v_\mathrm{p} =\, \frac{6}{4}\,\mathrm{m \cdot s^{−1} }=\, 1{,}5\,\mathrm{m \cdot s^{−1} }\),
C: uražená dráha \(s_4 =\, 10 \,\mathrm{m}\), \(v_\mathrm{p} =\, \frac{10}{4}\,\mathrm{m \cdot s^{−1} }=\, 2{,}5\,\mathrm{m \cdot s^{−1} }\),
D: uražená dráha \(s_4 =\, 10 \,\mathrm{m}\), \(v_\mathrm{p} =\, \frac{10}{4}\,\mathrm{m \cdot s^{−1} }=\, 2{,}5\,\mathrm{m \cdot s^{−1} }\).
c) Graf A, B, C: Rychlost se s časem nemění. Okamžitá rychlost je tedy rovna průměrné rychlosti spočítané v b).
Rychlost je daná sklonem přímek – jejich směrnicí.
Graf D:
Dráha rovnoměrně zrychleného přímočarého pohybu je daná vztahem:
\[s=\,\frac{at^{2} }{2}\,.\](Dráha a rychlost v čase t = 0 s byla rovna nule.)
Z grafu odečteme:
v čase \(t = 4\,\mathrm{s}\) je \(s(4)=10\,\mathrm{m}\) .
Platí tedy:
\[10\,\mathrm{m}\,=\,\frac{a \cdot 4^{2}\,\mathrm{s^{2}}}{2}.\]Odtud:
\[a=1{,}25\,\mathrm{m \cdot s^{−2} }.\]Pro okamžitou rychlost platí:
\[v=at= (1{,}25 {\cdot} 4)\,\mathrm{m \cdot s^{−1}}=\, 5\,\mathrm{m \cdot s^{−1} }.\]d) Z odpovědí v předchozích částech víme, jak se s časem mění rychlost u jednotlivých pohybů, a známe i její velikost v určitém čase. Stačí to jen zakreslit do grafu.
Grafy závislostí rychlostí na čase jednotlivých pohybů:
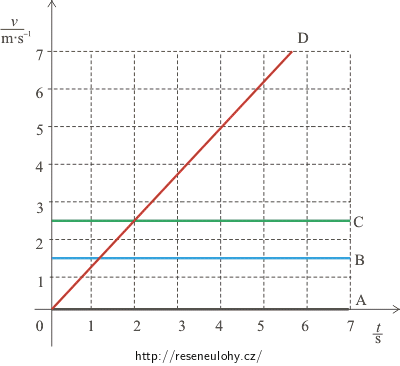
Rychlost autíček A, B, C se s časem neměnila:
Pohyb autíčka A: \(v_\mathrm{A} =\, 0\).
Pohyb autíčka B: \(v_\mathrm{B} =\, 1{,}5\,\mathrm{m \cdot s^{−1} }\).
Pohyb autíčka C: \(v_\mathrm{C} =\, 2{,}5\,\mathrm{m \cdot s^{−1} }\).
Pohyb autíčka D:
Z grafu závislosti dráhy na čase:
\[s=\,\frac{at^{2} }{2},\] \[10\,\mathrm{m} \,=\,\frac{a \cdot 4^{2}\,\mathrm{s^{2}}}{2},\] \[a=\,1{,}25\,\mathrm{m \cdot s^{−2} }.\]Pro závislost rychlosti na čase platí:
\[v=at\,,\] \[v=1{,}25\,\mathrm{m \cdot s^{−2} }\cdot t\,.\]e) Vyjádříme matematicky závislosti dráhy na čase s(t) dané grafem. (Pro graf D je odpověď v řešení bodu c)).
Pak zjistíme hodnotu dráhy pro t = t1 = 10 s.
A: Autíčko je stále v klidu:
\[s_0=s_1=\,10\,\mathrm{m}\,.\]B: Jedná se o rovnoměrný přímočarý pohyb s nenulovou počáteční dráhou:
\[s_1=s_0+v_\mathrm{B}t_1=\,(4+1{,}5{\cdot} 10)\,\mathrm{m}\,=19\,\mathrm{m}\,.\]C: Jedná se o rovnoměrný přímočarý pohyb s nulovou počáteční dráhou:
\[s_1=v_\mathrm{C}t_1=(2{,}5.10)\,\mathrm{m}=25\,\mathrm{m}\,.\]D: Jedná se o rovnoměrně zrychlený pohyb s nulovou počáteční dráhou:
\[s_1=\frac{at_1^{2}}{2}=\frac{(1{,}25{\cdot} 100)\,\mathrm{m} }{2}=62{,}5\,\mathrm{m}\,.\]Odpověď
a) A: Autíčko je v klidu. B, C: Jedná se o rovnoměrný přímočarý pohyb. D: Jedná se o pohyb rovnoměrně zrychlený přímočarý. b) A: Průměrná velikost rychlosti v časovém intervalu od 0 s do 4 s je nulová. B: Průměrná velikost rychlosti v časovém intervalu od 0 s do 4 s je 1,5 m·s−1. C: Průměrná velikost rychlosti v časovém intervalu od 0 s do 4 s je 2,5 m·s−1. D: Průměrná velikost rychlosti v časovém intervalu od 0 s do 4 s je 2,5 m·s−1. c) A: Okamžitá rychlost v čase 4 s je nulová. B: Velikost okamžité rychlosti v čase 4 s je 1,5 m·s−1. C: Velikost okamžité rychlosti v čase 4 s je 2,5 m·s−1. D: Velikost okamžité rychlosti v čase 4 s je 5 m·s−1. d)

e) A: Celková uražená dráha v čase 10 s je 10 m. B: Celková uražená dráha v čase 10 s je 19 m. C: Celková uražená dráha v čase 10 s je 25 m. D: Celková uražená dráha v čase 10 s je 62,5 m.





