Střela
Úloha číslo: 13
Střela o hmotnosti 10 g byla vypálena proti nepohyblivému dřevěnému kvádru o hmotnosti 1 kg, v němž pronikla do hloubky 10 cm. Do jaké hloubky by střela pronikla v kvádru, kdyby byl volně pohyblivý? Předpokládejme, že odpor, který dřevo klade pohybu střely, je stálý.
Zápis
m = 10 g hmotnost střely M = 1 kg = 1 000 g hmotnost kvádru h1 = 10 cm hloubka, do které střela pronikla h2 = ? hloubka, do které by střela pronikla, pokud by byl kvádr pohyblivý Nápověda 1 – zákony zachování
K řešení úlohy využijte zákon zachování energie a hybnosti.
Nápověda 2 – nepohyblivý kvádr
Co se děje s kinetickou energií střely v případě nepohyblivého kvádru. Zapište to rovnicí.
Nápověda 3 – volně pohyblivý kvádr
Rozepište ZZH a ZZE pro případ volně pohyblivého kvádru.
Nápověda 4 – hledaná hloubka
Získali jste 3 rovnice (1),(2),(3), vyjádřete z nich neznámou hloubku h2.
Číselný výpočet
m = 10 g hmotnost střely M = 1 kg = 1 000 g hmotnost kvádru h1 = 10 cm hloubka, do které střela pronikla h2 = ? hloubka, do které by střela pronikla, pokud by byl kvádr pohyblivý
\[h_{2}\,=\,\frac{h_{1}M}{m+M}\] \[h_{2}\,=\,\frac{10\,\cdot\,1\,000}{10\,+\,1\,000}\, \mathrm{cm}\] \[h_{2}\,\dot=\,9{,}9\,\mathrm{cm}\]Odpověď
V případě volně pohyblivého kvádru by střela pronikla do hloubky \[h_{2}=\frac{h_{1}M}{m+M}=9{,}9\,\mathrm{cm}.\]
Celkové řešení
K řešení úlohy využijeme zákony zachování hybnosti a energie.
Zákon zachování hybnosti (ZZH):
Součet hybností těles v izolované soustavě je konstantní, nebo-li celková hybnost izolované soustavy se zachováva.
Zákon zachování energie (ZZE):
Celková energie izolované soustavy se zachovává.
Nepohyblivý kvádr:
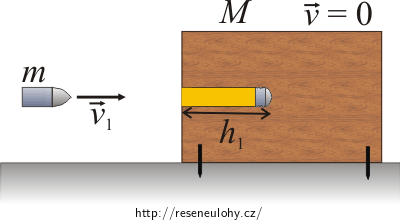
V případě nepohyblivého kvádru je kinetická energie střely před zásahem rovna práci, kterou vykoná odporová síla F při jejím zabrždění na dráze h1. Kinetická energie střely se mění na vnitřní energii dřeva a střely, což se projeví jejich zahřátím.
\[\frac{1}{2}mv_{1}^{2}\,=\,Fh_{1}\] \[F\,=\,\frac{mv_{1}^{2}}{2h_{1}}\tag{1}\]F … odporová síla
m … hmotnost střely
v1 … rychlost střely
h1 … hloubka, do které střela pronikne v případě nepohyblivého kvádru
Volně pohyblivý kvádr:
V případě volně pohyblivého kvádru platí:
\[\mathrm{ZZH:} \qquad \vec p_{1}+ \vec p_{2}\,=\, \vec p_{1}^{'}+ \vec p_{2}^{'}\,,\] kde\(\qquad \vec p_{1}\)… vektor hybnosti střely před nárazem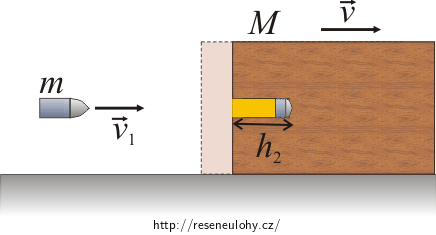
\(\vec p_{2}\)… vektor hybnosti kvádru před nárazem\(\vec p_{1}^{'}\)… vektor hybnosti střely po nárazu\(\vec p_{2}^{'}\)… vektor hybnosti kvádru po nárazu\[m\vec v_1+0\,=\,(M+m)\vec{v}\]skalárně:
\[mv_1\,=\,(M+m)v\,,\tag{2}\]kde m… hmotnost střely
v1… rychlost střely před nárazem
M… hmotnost kvádru
v… výsledná rychlost soustavy vzniklé spojením kvádru a střely.
\[ZZE:\]Střela se zaryje do kvádru do hloubky h2 a kvádr se střelou se bude pohybovat po zarytí rychlostí v. Počátěční kinetická energie střely se přemění jednak na práci odporové síly při zarytí střely do hloubky h2, což se projeví zahřátím střely a kvádru, a na kinetickou energii kvádru a střely.
\[\frac{1}{2}mv_{1}^{2}\,=\,Fh_{2}+\frac{1}{2}(m+M)v^{2}\,,\tag{3}\]kde F… odporová síla
h2… hloubka, do které pronikla střela v případě volně pohyblivého kvádru
Ze vztahu (2) si vyjádříme výslednou rychlost soustavy:
\[v\,=\,\frac{mv_{1}}{m\,+\,M}\,.\tag{4}\]Do rovnice (3) dosadíme získané vztahy pro výslednou rychlost (4) a pro odporovou sílu (1):
\[\frac{1}{2}mv_{1}^{2}\,=\,\frac{mv_{1}^{2}}{2h_{1}}h_{2}\,+\,\frac{1}{2}(m\,+\,M)\frac{m^{2}v_{1}^{2}}{\left(m\,+\,M\right)^{2}}\,.\]Vynásobíme celou rovnici dvěma:
\[mv_{1}^{2}\,=\,\frac{mv_{1}^{2}}{h_{1}}h_{2}\,+\,(m\,+\,M)\frac{m^{2}v_{1}^{2}}{\left(m\,+\,M\right)^{2}}\,.\]Víme, že rychlost střely před zarytím v1 je nenulová, a proto jí můžeme celou rovnici vydělit.
Dostaneme:
\[m\,=\,\frac{m}{h_{1}}h_{2}\,+\,\left(m\,+\,M\right)\frac{m^{2}}{(m\,+\,M)^{2}}\,.\]Úpravami získame tvar:
\[m\,=\,\frac{m}{h_{1}}h_{2}\,+\,\frac{m^{2}}{\left(m\,+\,M\right)}\,.\]Rovnici vydělíme hmotností střely:
\[1\,=\,\frac{h_{2}}{h_{1}}\,+\,\frac{m}{\left(m\,+\,M\right)}\,.\]Vynásobíme celou rovnici h1:
\[h_{1}\,=\,h_{2}\,+\,\frac{h_{1}m}{m\,+\,M}\,.\]Převedeme zlomek \[\frac{h_{1}m}{m\,+\,M}\] na druhou stranu a vytkneme h1 před závorku:
\[h_{2}\,=\,h_{1}\left(1\,-\,\frac{m}{m\,+\,M}\right)\,.\]Upravíme výraz v závorce tak, že jej převedeme na společný jmenovatel:
\[h_{2}\,=\,h_{1}\left(\frac{m\,+\,M\,-\,m}{m\,+\,M}\right)\,=\,\frac{h_{1}M}{m\,+\,M}\,.\] \[h_{2}\,=\,\frac{10\,\cdot\,1\,000}{10\,+\,1\,000}\,\mathrm{cm}\] \[h_{2}\,\dot=\,9{,}9\,\mathrm{cm}\]Odpověď: V případě volně pohyblivého kvádru by střela pronikla do hloubky 9,9 cm.
