Hustota koule
Úloha číslo: 1029
Koule o hmotnosti 5,67 kg je ponořena do vody a napíná lano, na kterém visí, silou o velikosti 50,7 N. Určete hustotu koule.
Zápis
m = 5,67 kg hmotnost koule F = 50,7 N síla napínající závěsné lano ρ = ? hustota koule Nápověda 1
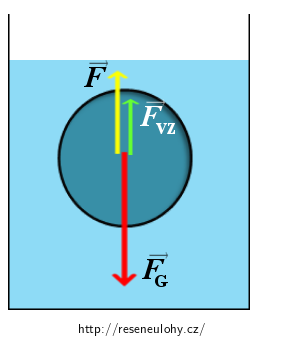
Jaké síly na kouli ponořenou ve vodě působí? Jaký mají směr? Zakreslete je do obrázku.
Nápověda 2
Co platí pro výslednici těchto sil? (Připomeňte si 1. Newtonův zákon.) Zapište vztah vektorově i pro velikosti jednotlivých sil.
Nápověda 3 – určení tíhové a vztlakové síly
Ve vztahu (1) známe pouze sílu F, zbylé dvě síly musíme dopočítat. Jak určíte tíhovou a vztlakovou sílu?
Nápověda 4
Dosaďte vztahy pro tíhovou a vztlakovou sílu do rovnice (1) a vyjádřete z ní hledanou hustotu.
Celkové řešení
Na kouli působí následující tři síly:
- tíhová síla FG svisle dolů,
- vztlaková síla Fvz svisle vzhůru,
- síla závěsného lana F svisle vzhůru.
Protože koule je vzhledem k nádobě (či experimentátorovi) v klidu, je podle 1. Newtonova zákona výslednice sil na ni působící nulová, tj.:
\[\vec{F}_\mathrm{G}\,+\,\vec{F}_\mathrm{vz}\,+\,\vec{F}\,=\,\vec{o}\,. \]Protože tíhová síla má opačný směr než zbylé dvě síly, lze pro velikosti sil psát:
\[-F_\mathrm{G}\,+\,F_\mathrm{vz}\,+\,F\,=\,0\,\Rightarrow\,F_\mathrm{G}\,=\,F_\mathrm{vz}\,+\,F\,.\tag{1}\]Tíhovou sílu určíme snadno jako:
\[F_\mathrm{G}\,=\,mg\,,\tag{2}\]kde m je hmotnost koule a g tíhové zrychlení.
Také pro výpočet vztlakové síly použijeme známý vztah:
\[F_\mathrm{vz}\,=\,V{\rho}_\mathrm{k}g\,,\tag{3}\]kde V je objem ponořené části tělesa, ρk hustota kapaliny – v našem případě vody – a g opět tíhové zrychlení.
Ve vztahu (3) ovšem stále neznáme objem ponořené koule, a protože není zadán její poloměr, použijeme k výpočtu objemu definiční vztah pro hustotu:
\[{\rho}\,=\,\frac{m}{V}\,\Rightarrow\,V\,=\,\frac{m}{{\rho}}\,,\tag{4}\]kde m je hmotnost koule a ρ její hustota. Dosazením vztahu (4) do vztahu (3) dostáváme rovnici pro výpočet vztlakové síly, ve které figuruje už pouze jediná neznámá – hledaná hustota koule:
\[F_\mathrm{vz}\,=\,V{\rho}_\mathrm{k}g\,=\,\frac{m}{{\rho}}{\rho}_\mathrm{k}g\,.\tag{5}\]Dosazením vztahů (2) a (5) do rovnice (1) dostáváme:
\[mg\,=\,\frac{m}{\rho}{\rho}_\mathrm{k}g\,+\,F\,.\] Úpravou: \[\rho\,=\,\frac{m{\rho}_\mathrm{k}g}{mg\,-\,F}\,.\] Číselně: \[\rho\,\dot=\,\frac{5{,}67{\cdot}1000{\cdot}9{,}81}{5{,}67{\cdot}9{,}81\,-\,50{,}7}\,\mathrm{kg{\cdot}m^{-3}}\,\dot=\,11\,300\,\mathrm{kg{\cdot}m^{-3}}\,.\]Odpověď
Hustota koule je přibližně 11 300 kg·m-3. Tato hodnota hustoty odpovídá hustotě olova.