Náboj ve vakuu
Úloha číslo: 129
Náboj byl vystřelen ve vakuu vodorovně rychlostí o velikosti v0. Určete závislost velikosti rychlosti v a velikosti tečného at a normálového zrychlení an na čase t tohoto pohybu.
Odvoďte i průběh poloměru křivosti ρ trajektorie v závislosti na čase t.
Nápověda 1: Obrázek situace
Nakreslete obrázek situace a označte si souřadnicové osy x a y.
Do obrázku vyznačte vektor počáteční rychlosti náboje \(\vec{v}_0\) a jeho rychlost \(\vec{v}\) v libovolném bodě pohybu i její složky ve směru souřadnicových os.
Nápověda 2: Průběh velikosti rychlosti
Rozmyslete si, jakým pohybem se náboj pohybuje ve směru souřadnicových os.
Vyjádřete si nejprve složky rychlosti náboje vx, vy. Z nich pak snadno zjistíte průběh velikosti rychlosti náboje.
Nápověda 3: Velikost tečného zrychlení
Využijte znalost průběhu velikosti rychlosti náboje z předchozí nápovědy. Jak z něj vyjádříte velikost tečného zrychlení náboje?
Nápověda 4: Velikost normálového zrychlení
Pro určení velikosti normálového zrychlení náboje budete potřebovat kromě velikosti jeho tečného zrychlení (znáte z předchozí nápovědy) také velikost jeho celkového zrychlení. To získáte ze složek zrychlení ax, ay ve směru souřadnicových os.
Víte, jaký platí vztah mezi celkovým, tečným a normálovým zrychlením náboje?
Nápověda 5: Poloměr křivosti trajektorie
Trajektorii pohybu náboje máte naznačenu v obrázku situace.
Jaký je vztah mezi poloměrem křivosti trajektorie, velikostí rychlosti a normálového zrychlení náboje?
CELKOVÉ ŘEŠENÍ:
Obrázek situace:
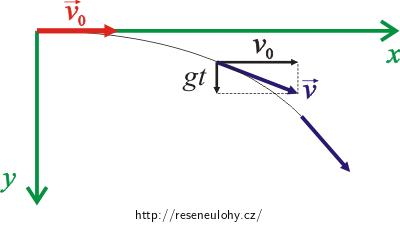
Ve směru osy x: Rovnoměrný přímočarý pohyb rychlosti o velikosti v0.
Ve směru osy y: Volný pád.
Velikost rychlosti:
Složky rychlosti (ve směru osy x a osy y ):
\[v_\mathrm{x}\,=\,v_0\,,\] \[v_\mathrm{y}=gt\,.\]Průběh velikosti rychlosti:
\[v(t) \,=\, \sqrt{v_\mathrm{x}^{2}\,+\,v_\mathrm{y}^{2}}\,=\,\sqrt{v_0^{2}\,+\,g^{2}t^{2}}\,.\]Velikost tečného zrychlení:
Velikost tečného zrychlení získáme časovou derivací velikosti celkové rychlosti:
\[a_\mathrm{t}\,=\,\frac{\mathrm{d}v}{\mathrm{d}t}\,=\,\frac{\mathrm{d}\left(\sqrt{v_0^{2}+g^{2}t^{2}}\right)}{\mathrm{d}t}\,=\,\frac{g^{2}t}{ \sqrt{v_0^{2}+g^{2}t^{2}}}\,.\]Velikost normálového zrychlení:
Velikost normálového zrychlení získáme ze vztahu:
\[a_\mathrm{c}\,=\,\sqrt{a_\mathrm{t}^{2}+ a_\mathrm{n}^{2}}\,.\]Odtud:
\[a_\mathrm{n}\,=\,\sqrt{a_\mathrm{c}^{2}-a_\mathrm{t}^{2}}\,.\]Složky celkového zrychlení:
\[a_\mathrm{x}\,=\,\frac{\mathrm{d}v_\mathrm{x}}{\mathrm{d}t}\,=\,\frac{\mathrm{d}(v_0)}{\mathrm{d}t} \,=\, 0\,,\] \[a_\mathrm{y}\,=\,\frac{\mathrm{d}v_\mathrm{y}}{\mathrm{d}t}\,=\, \frac{\mathrm{d}(gt)}{\mathrm{d}t} \,=\, g\,,\]\[a_\mathrm{c} \,=\, \sqrt{a_\mathrm{x}^{2}+ a_\mathrm{y}^{2}} \,=\, g\,,\] \[a_\mathrm{n}\,=\,\sqrt{g^{2}-\frac{g^{4}t^{2}}{v_0^{2}+g^{2}t^{2}}} \,=\, \sqrt{\frac{g^{2}v_0^{2}}{v_0^{2}+g^{2}t^{2}}}\,,\] \[a_\mathrm{n}\,=\,\frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\, .\]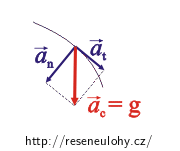
Poloměr křivosti trajektorie:
Pro velikost normálového zrychlení platí:
\[a_\mathrm{n} \,=\,\frac{v^{2}}{\rho}\,.\]Pro poloměr křivosti trajektorie pak platí:
\[\rho\,=\,\frac{v^{2}}{a_\mathrm{n}}\,,\]kde
\[v \,=\, \sqrt{v_0^{2}+g^{2}t^{2}}\,,\] \[a_\mathrm{n}\,=\,\frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\,.\] \[\rho(t)\,=\,\frac{ (v_0^{2}+g^{2}t^{2})\sqrt{v_0^{2}+g^{2}t^{2}}}{gv_0}\,=\,\frac{\sqrt{( v_0^{2}+g^{2}t^{2})^{3}}}{gv_0}\,.\]Odpověď
Průběh velikosti rychlosti náboje je
\[v(t) \,=\, \sqrt{v_0^{2}+g^{2}t^{2}}\,.\]Velikost tečného zrychlení náboje je
\[a_\mathrm{t}(t) \,=\, \frac{g^{2}t}{ \sqrt{v_0^{2}+g^{2}t^{2}}}\,.\]Velikost normálového zrychlení náboje je
\[a_\mathrm{n}(t) \,=\, \frac{gv_0}{\sqrt{v_0^{2}+g^{2}t^{2}}}\,.\]Pro poloměr křivosti trajektorie náboje platí
\[\rho(t) \,=\, \frac{\sqrt{( v_0^{2}+g^{2}t^{2})^{3}}}{v_0g}\,.\]




