Kutálející se obruč
Úloha číslo: 528
Zápis
m = 10 kg hmotnost obruče r = 0,5 m poloměr obruče α = 30° úhel, který svírá nakloněná rovina s vodorovnou rovinou s = 5 m uběhnutá dráha v = ? (m·s−1) rychlost těžiště Rozbor
Úlohu je možné řešit dvěma způsoby. Buď pomocí zákona zachování mechanické energie (A), nebo přes impulsové věty (B).
V prvním případě je třeba zvolit dvě vhodné situace, ve kterých budete mechanickou energii obruče srovnávat. Uvědomte si, že obruč se jednak otáčí kolem svého těžiště, jednak koná posuvný pohyb.
Při řešení přes impulsové věty je třeba uvážit, které všechny síly na obruč působí, co platí pro jejich výslednici a co platí pro výslednici momentů těchto sil. Je třeba také zvážit, vzhledem ke kterému bodu budete momenty sil psát, a s ohledem na to napsat správný vztah pro moment setrvačnosti obruče vzhledem k ose procházející tímto bodem.
1. a 2. věta impulsová (a něco navíc)
1. věta impulsová (jako věta o pohybu hmotného středu soustavy) říká, že:
Hmotný střed soustavy se pohybuje jako hmotný bod o celkové hmotnosti soustavy, na který působí výslednice vnějších sil působících na soustavu.
\[\vec{F}_\mathrm{v} = m_\mathrm{s} \vec{a}\]2. věta impulsová říká, že:
Časová změna momentu hybnosti soustavy se rovná celkovému momentu vnějších sil.
\[\vec{M}=\frac{d\vec{L}}{dt}\](\(\vec{M}\) a \(\vec{L}\) jsou vztahovány k témuž bodu.)
V případě rotace tuhého tělesa kolem pevné osy platí:
\[L = J \omega\,,\] \[\vec{M}=\frac{d\vec{L}}{dt} = J\vec{\epsilon}\,,\]kde:
J … moment setrvačnosti tělesa vůči pevné ose otáčení,
\(\vec{\epsilon}\)… úhlové zrychlení (vektory \(\vec{\epsilon},\) \(\vec{M}\) míří ve směru osy otáčení).
Steinerova věta:
\[J = J_\mathrm{s} + mr^2\,,\]kde:
J … moment setrvačnosti tělesa vůči libovolné ose o,
Js … moment setrvačnosti vůči ose os procházející těžištěm tělesa (o je rovnoběžná s os),
m … hmotnost tělesa,
r … vzdálenost os o a os.
Königova věta:
Kinetická energie tělesa, které koná posuvný a otáčivý pohyb:
\[E_\mathrm{k} = \frac{1}{2}mv_\mathrm{s}^2 + \frac{1}{2}J_\mathrm{s}\omega^2\,,\]kde:
vs… rychlost hmotného středu S,
Js … moment setrvačnosti vůči ose procházející těžištěm tělesa.
Hmotný střed vs. těžiště
V úloze se mluví jednak o hmotném středu (popř. středu), jednak o těžišti. Autor má na mysli vždy ten samý bod.
V čem je rozdíl?
Těžiště je zavedeno jako působiště výsledné tíhové síly. Bez této síly nemá smysl o něm mluvit.
Naopak hmotný střed je dán matematicky. Jednoduše řečeno je souřadnice hmotného středu průměrem z souřadnic všech bodů tělesa, více zde.
Jejich polohy by se mohly lišit pouze ve značně nehomogenním tíhovém poli, například pokud by se náš problém odehrával v blízkosti drobné černé díry.
V praxi se s takovými problémy v podstatě nesetkáváme.
(Nemluvě o tom, že v blízkosti černých děr máme většinou jediný problém, a to jak dostatečně rychle utéci.)
Nápověda 1A
Vyberte dvě situace, ve kterých budete mechanickou energii obruče srovnávat. Nezapomeňte zvolit hladinu nulové potenciální energie.Nápověda 2A
Vyjádřete potenciální energii obruče v situaci (1) a kinetickou energii obruče v situaci (2). Dosaďte do vztahu (1) a odtud pak získáte hledanou rychlost.
Nápověda 1B
Nakreslete do obrázku všechny síly, které na obruč působí. Napište, co platí pro jejich výslednici.Nápověda 2B
Zvolte bod, vzhledem ke kterému budete vztahovat momenty působících sil, a napište, co pro ně platí.
Nápověda 3B
Pomocí rovnic (2) a (3) vyjádřete zrychlení obruče a odtud pak hledanou rychlost.
Komentář
Momenty působících sil můžeme vztahovat i k jinému bodu, např. bodu Q styku obruče s podložkou. Tím se vynuluje moment hned dvou sil, třecí a reakce podložky.
Zbývá moment síly tíhové:
\[\vec{M}=\vec{r}\times\vec{F}_\mathrm{g} = J_\mathrm{Q}\vec{\epsilon}.\]Přepíšeme skalárně:
\[M=F_\mathrm{g}r\sin\alpha= J_\mathrm{Q}\epsilon\,,\] \[mgr\sin\alpha = J_\mathrm{Q} \frac{a}{r}\,.\]Moment setrvačnosti obruče o hmotnosti m vzhledem k ose procházející středem je \(J=mr^2\), ovšem bod dotyku je od osy procházející středem vzdálen r, takže podle Steinerovy věty:
\[J_\mathrm{Q}=J+md^2=mr^2+mr^2=2mr^2\,.\]Pak:
\[mgr\sin\alpha = 2mr^2\frac{a}{r}\,.\]Odtud:
\[a = \frac{1}{2}g\sin\alpha\,.\]Dále je řešení stejné jako u nápovědy 3B.
Číselné dosazení
\[\alpha=30^{\circ}\] \[\sin\alpha=0{,}5\] \[s=5\,\mathrm{m}\] \[g=9{,}81\,\mathrm{m\cdot s^{-2}}\] \[v=\sqrt{gs \sin\alpha}=\sqrt{9{,}81{\cdot}5\cdot0{,}5} \,\mathrm{m\cdot s^{-1}}\dot{=}5 \,\mathrm{m\cdot s^{-1}}\]Celkové řešení pomocí zákona zachování mechanické energie
Vybereme dvě situace, ve kterých budeme mechanickou energii obruče srovnávat.
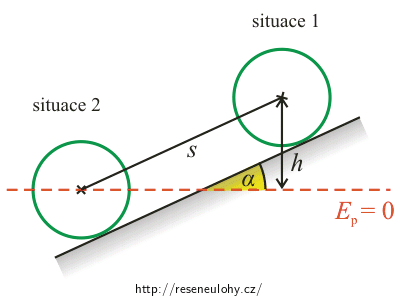
Všimneme si energie kinetické Ek0 a potenciální Ep0 na počátku pohybu a po uběhnutí dráhy s: Ek, Ep.
Podle zákona zachování mechanické energie platí:
\[E_\mathrm{k0}+E_\mathrm{p0} = E_\mathrm{k}+ E_\mathrm{p}\,.\]Rychlost na počátku je nulová, proto je:
\[E_\mathrm{k0}=0\,.\]Zvolíme hladinu nulové potenciální energie tak, aby byla po uražení dráhy s nulová:
\[E_\mathrm{p}=0\,.\]Platí tedy:
\[E_\mathrm{p0} = E_\mathrm{k}\,.\tag{1}\]Pro potenciální energii v situaci (1) platí
\[E_\mathrm{p0}=mgh\,,\]kde h, tedy rozdíl výšky, je v tomto případě
\[h=s\sin\alpha\,.\]Kinetická energie v situaci (2) se skládá ze dvou složek, a to energie otáčení obruče kolem středu a energie posuvného pohybu těžiště.
\[E_\mathrm{k}=\frac{1}{2} J\omega^2+ \frac{1}{2} mv^2.\]Moment setrvačnosti obruče vůči ose procházející středem je \(J=mr^2\).
Pro úhlovou rychlost otáčení obruče platí:
\[\omega=\frac{v}{r}.\]Postupně dosadíme do vztahu (1):
\[E_\mathrm{p0}=E_\mathrm{k}\,,\] \[mgh=\frac{1}{2} J\omega^2+ \frac{1}{2} mv^2\,,\] \[mgs \sin\alpha= \frac{1}{2} mr^2(\frac{v}{r})^2+\frac{1}{2}mv^2\,.\]Vydělíme m a sečteme pravou stranu:
\[gs \sin\alpha=v^2\,,\] \[v=\sqrt{gs \sin\alpha}\,.\]Celkové řešení pomocí impulsových vět
Nakreslíme do obrázku všechny síly, které na obruč působí. Napíšeme, co platí pro jejich výslednici.
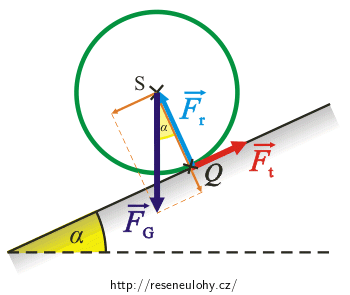
\(\vec{F}_\mathrm{g}\)...síla tíhová
\(\vec{F}_\mathrm{r}\)...tlaková síla, kterou působí podložka
\(\vec{F}_\mathrm{t}\)...klidová třecí síla, neboť obruč nepodkluzuje
Pro výslednici sil platí:
\[\vec{F}_\mathrm{g} + \vec{F}_\mathrm{t} + \vec{F}_\mathrm{r} = m\vec{a}\,,\]kde \(\vec{a}\) je zrychlení těžiště.
Přepíšeme skalárně. Osu x volíme ve směru pohybu těžiště, osu y kolmo na ni:
\[x: \hspace{10px} mgsin\alpha - F_\mathrm{t} = ma,\tag{1}\] \[y: \hspace{15px} F_\mathrm{r} - mg cos\alpha = 0\]Zvolíme bod, vzhledem ke kterému budeme vztahovat momenty působících sil, a napíšeme, co pro ně platí.
Vzhledem k bodu S:
Moment \(\vec{F}_\mathrm{g}\) a \(\vec{F}_\mathrm{r}\) je nulový. Takže:
\[\vec{M}=\vec{r}\times\vec{F}_\mathrm{t} = J\vec{\epsilon}\,.\]Přepíšeme skalárně:
\[F_\mathrm{t}r = J\epsilon = J \frac{a}{r}\,.\]Pro moment setrvačnosti platí: \(J = mr^2\). Pak:
\[F_\mathrm{t}r = mr^2\frac{a}{r}\,.\]Odtud:
\[F_\mathrm{t} = ma\,.\tag{2}\]Pomocí rovnic (1) a (2) vyjádříme zrychlení obruče a odtud pak hledanou rychlost.
Z (2) dosadíme za Ft do (1):
\[mg\sin\alpha = 2ma\,.\]Vydělíme m:
\[a = \frac{1}{2}g\sin\alpha\,.\tag{3}\]Pro uraženou dráhu platí:
\[s=\frac{1}{2}at^2\,,\]kde:
\[v=at\,.\]Odtud:
\[s=\frac{1}{2}a\frac{v^2}{a^2}\,,\] \[v^2 = 2sa\,,\] \[v=\sqrt{2sa}\,.\]Dosadíme z (3):
\[v=\sqrt{2s\frac{1}{2}g\sin\alpha}\,,\] \[v=\sqrt{gs\sin\alpha}\,.\]Odpověď
Rychlost těžiště obruče je:
\[v=\sqrt{gs \sin\alpha}\,.\]Číselně:
\[v \,\dot{=}\,5 \,\mathrm{m\cdot s^{-1}}\,.\]




