Sbírka řešených úloh

Klouzání úsečky II

Úloha číslo: 190

Úsečka AB konstantní délky l se pohybuje tak, že její koncové body kloužou po y-ové, resp. x-ové ose pravoúhlé soustavy souřadnic. (Obrázek ukazuje situaci v 1. kvadrantu.)

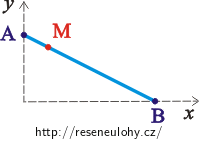
Zjistěte, jakou trajektorii bude při tomto pohybu opisovat libovolný bod M uvedené úsečky.

• Komentář: Podobný příklad

  Už jste vyřešili úlohu Klouzání úsečky I? Tato úloha se řeší podobným způsobem.

• Nápověda 1

  Určete obecně souřadnice bodů A, B. Znáte nějaký vztah, který je spojuje s délkou l úsečky AB?

• Řešení k nápovědě 1

  Souřadnice bodů A, B:

  A = [0; y],

  B = [x; 0].

  S délkou l úsečky AB jsou tyto souřadnice spojeny Pythagorovou větou:

  \[x^2\,+\,y^2\,=\,l^2.\tag{1}\]

• Nápověda 2

  Zajímají nás souřadnice bodu M − pokuste se pomocí nich vyjádřit souřadnice bodů A, B. Uvědomte si, že bod M leží na přímce vytyčené body A, B (označme tuto přímku například p). Pro nějakou hodnotu parametru tedy musí bod M splňovat parametrické rovnice přímky p.

• Řešení k nápovědě 2

  Označme souřadnice bodu M = [x_m; y_m].

  Přímku p popíšeme parametricky pomocí bodu A = [0; y] a jejího směrového vektoru \(\vec{u}\) = B − A = (x; −y).

  Pro každý bod X = [x₀; y₀] přímky p pak platí:

  \(X\,=\,A\,+\,s\cdot\vec{u}\), tedy:

  \(x_0\,=\,0\,+\,s\cdot x\,=\,s\cdot x,\)

  \(y_0\,=\,y\,+\,s\cdot (-y)\,=\,(1-s)\cdot y,\)

  kde s je libovolný reálný parametr.

  Speciálně pak pro bod M:

  \[x_\mathrm{m}\,=\,s_\mathrm{m}\cdot x,\tag{2}\]

  \[y_\mathrm{m}\,=\,(1-s_\mathrm{m})\cdot y,\tag{3}\]

  kde s_m je libovolný reálný parametr z intervalu (0, 1).

  Zúžením definičního oboru parametru se z celé přímky omezujeme pouze na vnitřní body úsečky AB. (Můžete vyzkoušet, že pro s_m = 0 dostáváme bod A, pro s_m = 1 bod B a pro 0<s_m<1 bod mezi A a B.) Číselnou volbou s_m dostáváme podmínky pro konkrétní bod M − např. pro s_m = 0,5 by to byl střed úsečky AB (viz úloha Klouzání úsečky I).

  Z rovnic (2) a (3) nyní již snadno vyjádříme souřadnice bodů A, B pomocí souřadnic bodu M:

  \[x\,=\,\frac{x_\mathrm{m}}{s_\mathrm{m}}\,\rightarrow\,B\,=\,[\frac{x_\mathrm{m}}{s_\mathrm{m}};\,0],\]

  \[y\,=\,\frac{y_\mathrm{m}}{1-s_\mathrm{m}}\,\rightarrow\,A\,=\,[0;\,\frac{y_\mathrm{m}}{1-s_\mathrm{m}}].\]

• Nápověda 3

  Dosaďte vyjádřené souřadnice bodů A, B do vztahu (1) a upravte. Jakou křivku popisuje vzniklá rovnice?

• Řešení k nápovědě 3

  Dosadíme do vztahu (1) souřadnice bodů A, B vyjádřené pomocí souřadnic bodu M:

  \[x^2\,+\,y^2\,=\,l^2\,,\]

  \[(\frac{x_\mathrm{m}}{s_\mathrm{m}})^2\,+\,(\frac{y_\mathrm{m}}{1-s_\mathrm{m}})^2\,=\,l^2\,,\]

  \[\frac{x_\mathrm{m}^2}{(s_{\mathrm{m}}l)^2}\,+\,\frac{y_\mathrm{m}^2}{[(1-s_\mathrm{m})l]^2}\,=\,1\,,\]

  což je rovnice elipsy se středem v počátku, délkou hlavní poloosy s_ml a délkou vedlejší poloosy (1−s_m)l.

• Celkové řešení

  Určíme souřadnice bodů A, B:

  A = [0; y],

  B = [x; 0].

  S délkou l úsečky AB jsou tyto souřadnice spojeny Pythagorovou větou:

  \[x^2\,+\,y^2\,=\,l^2.\tag{1}\]

  Označme souřadnice bodu M = [x_m; y_m].

  Přímku p určenou body A, B popíšeme parametricky pomocí bodu A = [0; y] a jejího směrového vektoru \(\vec{u}\) = B − A = (x; −y).

  Pro každý bod X = [x₀; y₀] přímky p pak platí:

  \(X\,=\,A\,+\,s\cdot\vec{u}\), tedy:

  \(x_0\,=\,0\,+\,s\cdot x\,=\,s\cdot x,\)

  \(y_0\,=\,y\,+\,s\cdot (-y)\,=\,(1-s)\cdot y\,,\)

  kde s je libovolný reálný parametr.

  Speciálně pak pro bod M:

  \[x_\mathrm{m}\,=\,s_\mathrm{m}\cdot x,\tag{2}\]

  \[y_\mathrm{m}\,=\,(1-s_\mathrm{m})\cdot y,\tag{3}\]

  kde s_m je libovolný reálný parametr z intervalu (0, 1).

  Zúžením definičního oboru parametru se z celé přímky omezujeme pouze na vnitřní body úsečky AB. (Můžete vyzkoušet, že pro s_m = 0 dostáváme bod A, pro s_m = 1 bod B a pro 0<s_m<1 bod mezi A a B.) Číselnou volbou s_m dostáváme podmínky pro konkrétní bod M − např. pro s_m = 0,5 by to byl střed úsečky AB (viz úloha Klouzání úsečky I).

  Z rovnic (2) a (3) nyní již snadno vyjádříme souřadnice bodů A, B pomocí souřadnic bodu M:

  \[x\,=\,\frac{x_\mathrm{m}}{s_\mathrm{m}}\,\rightarrow\,B\,=\,[\frac{x_\mathrm{m}}{s_\mathrm{m}};\,0],\]

  \[y\,=\,\frac{y_\mathrm{m}}{1-s_\mathrm{m}}\,\rightarrow\,A\,=\,[0;\,\frac{y_\mathrm{m}}{1-s_\mathrm{m}}].\]

  Dosadíme do vztahu (1) souřadnice bodů A, B vyjádřené pomocí souřadnic bodu M:

  \[x^2\,+\,y^2\,=\,l^2\,,\]

  \[(\frac{x_\mathrm{m}}{s_\mathrm{m}})^2\,+\,(\frac{y_\mathrm{m}}{1-s_\mathrm{m}})^2\,=\,l^2\,,\]

  \[\frac{x_\mathrm{m}^2}{(s_\mathrm{m}l)^2}\,+\,\frac{y_\mathrm{m}^2}{[(1-s_\mathrm{m})l]^2}\,=\,1\,,\]

  což je rovnice elipsy se středem v počátku, délkou hlavní poloosy s_ml a délkou vedlejší poloosy (1−s_m)l.

• Odpověď

  Trajektorií bodu je elipsa se středem v počátku, délkou hlavní poloosy s_ml a délkou vedlejší poloosy (1−s_m)l. (Omezíme-li se pouze na první kvadrant, který je znázorněn obrázkem, bude se jednat o čtvrtinu této elipsy.)

• Vizualizace pomocí apletu

  Kliknutím na tlačítko „Zapnout animaci“ se spustí animace klouzání úsečky po souřadnicových osách. Opětovné kliknutí animaci zastaví. Čas \(t\) je možné měnit na posuvníku. Tlačítko „Zapnout stopu“ zapíná/vypíná stopu bodu M. Po zaškrtnutí tlačítka „Zobrazit trajektorii“ se zobrazí trajektorie bodu M bez nutnosti vykreslení stopou bodu M. Tlačítko „Reset“ zastaví animaci a vrátí aplet do původního stavu.

   

   

  Z apletu je vidět, že bod M opisuje elipsu. Bodem M je ovšem možné libovolně posouvat po úsečce AB. Vyzkoušejte si, jaké další elipsy bude bod M opisovat pro různé polohy na úsečce AB.

   

• Podobná úloha

  Klouzání úsečky I je jednodušší obdobou této úlohy.