Hohmannova trajektorie
Úloha číslo: 1157
Země obíhá kolem Slunce přibližně po kružnici o poloměru \(149{,}6{\cdot}10^6 \mathrm{km}\), doba oběhu je \(365{,}25 \mathrm{dne}\). Také Mars obíhá kolem Slunce přibližně po kružnici a jeho doba oběhu je \(686{,}96 \mathrm{dne}\). Ze Země na Mars byly již vyslány kosmické lodi. Energeticky nejvýhodnější je tzv. Hohmannova trajektorie. Má tvar poloviny elipsy, která se ve výchozím bodě \(Z_{1}\) dotýká trajektorie Země a v koncovém bodě \(M_{2}\) trajektorie Marsu, přičemž tato místa musí ležet na opačných stranách od Slunce.
Historická poznámka
Německý vědec Walter Hohmann (1880-1945) přispěl k rozvoji nebeské mechaniky a teorie kosmických letů. Objevil energeticky výhodnou trajektorii, po které by se dal uskutečnit let mezi planetami. Tato trajektorie byla po něm nazvána Hohmannova.
Poznámka k obrázkům
V této úloze nejsou velikosti objektů v obrázcích v reálném poměru.
Zápis
\( r_\mathrm{Z}=149{,}6{\cdot}10^6 \mathrm{km}\) poloměr trajektorie, po které Země obíhá Slunce \(T_\mathrm{Z}=365{,}25 \mathrm{dne}=31 557 600 \mathrm{s}\) doba oběhu Země kolem Slunce \(T_\mathrm{M}=686{,}96 \mathrm{dne}=59 353 344 \mathrm{s}\) doba oběhu Marsu kolem Slunce \(Z_{1}\) poloha Země v okamžiku startu kosmické lodi \(M_{2}\) poloha Marsu v okamžiku přistání kosmické lodi a) \( r_\mathrm{M}= ? \mathrm{km}\) poloměr trajektorie, po které Mars obíhá Slunce \( v_\mathrm{M}= ? \mathrm{\frac{km}{s}}\) velikost rychlosti Marsu b) \( a= ? \mathrm{km}\) délka velké poloosy Hohmannovy trajektorie c) \( t= ? \mathrm{dne}\) doba letu kosmické lodi ze Země na Mars po Hohmannově trajektorii d) \(M_{1}\) poloha Marsu v okamžiku startu kosmické lodi e) \(Z_{2}\) poloha Země v okamžiku přistání kosmické lodi Nápověda a1) – poloměr trajektorie Marsu
K výpočtu poloměru trajektorie Marsu použijte třetí Keplerův zákon.
Nápověda a2) – velikost rychlosti Marsu
Využijte toho, že již znáte poloměr kružnice, po které obíhá Mars Slunce. Její délku jistě spočítáte. K určení velikosti rychlosti Marsu pak použijte ještě známou dobu oběhu.
Nápověda b1)
Nakreslete si obrázek trajektorií Země, Marsu a kosmické lodi a vyznačte v něm délku velké poloosy Hohmannovy trajektorie.
Nápověda b2)
Na základě obrázku, který je uvedený v „Řešení nápovědy b1)“, odvoďte vzorec pro výpočet délky velké poloosy Hohmannovy trajektorie.
Nápověda c)
K výpočtu doby letu kosmické lodi ze Země na Mars použijte třetí Keplerův zákon.
Nápověda d1) – úhel posunutí Marsu
Znáte dobu jednoho oběhu Marsu kolem Slunce a také dobu letu kosmické lodi. Určete, o jaký úhel se Mars posunul po své trajektorii za dobu od startu rakety do jejího přistání.
K výpočtu úhlu můžete využít například trojčlenku.
Nápověda d2) – úhel posunutí Země
Při určení úhlu posunutí Země postupujte podobně jako u Marsu.
Polohu Marsu v době startu kosmické lodi a polohu Země v době jejího přistání pak zakreslete do obrázku.
Celkové řešení
a) Poloměr trajektorie Marsu a velikost jeho rychlosti
Dle třetího Keplerova zákona vypočítáme poloměr trajektorie Marsu: \[\left(\frac{r_\mathrm{M}}{r_\mathrm{Z}}\right)^3=\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2.\] Obě strany rovnice vynásobíme \(r_\mathrm{Z}^3\): \[r_\mathrm{M}^3=r_\mathrm{Z}^3\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2.\] Obě strany rovnice odmocníme třetí odmocninou: \[r_\mathrm{M}=r_{Z}\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}.\tag{1}\]
Velikost rychlosti \(v\) Marsu vypočítáme dle vztahu: \[v=\frac{s}{T_\mathrm{M}},\tag{2}\] kde \(s\) je dráha, kterou Mars uběhne za dobu \(T_\mathrm{M}\).
Nejprve musíme vypočítat dráhu \(s\), kterou Mars uběhne za dobu \(T_\mathrm{M}\). Trajektorie Marsu je přibližně kruhová, bude tedy platit: \[s=2\pi r_\mathrm{M}.\tag{3}\] Do vztahu (2) dosadíme za \(s\) dle (3): \[v=\frac{2\pi r_\mathrm{M}}{T_\mathrm{M}}.\] Dosadíme za \(r_\mathrm{M}\) dle (1): \[v=\frac{2\pi r_\mathrm{Z}\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}}{T_\mathrm{M}}.\]
Číselné řešení:
\[r_\mathrm{M}=149{,}6{\cdot}10^6\sqrt[3] {\left(\frac{686{,}96}{365{,}25}\right)^2} \mathrm{km} \dot= 227{,}94{\cdot}10^6 \mathrm{km}.\]
\[v=\frac{2\pi 149{,}6{\cdot}10^6\sqrt[3] {\left(\frac{686{,}96}{365{,}25}\right)^2}}{59 353 344} \mathrm{\frac{km}{s}} \dot= 24{,}13 \mathrm{\frac{km}{s}}.\]
b) Délka velké poloosy Hohmannovy trajektorie
Nakreslíme si obrázek trajektorií Země, Marsu a kosmické lodi a vyznačíme v něm délku velké poloosy Hohmannovy trajektorie.
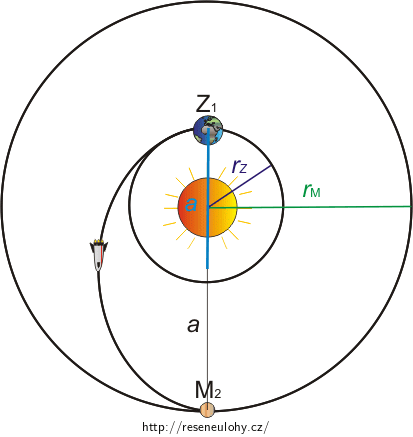
Z obrázku odvodíme, že bude platit: \[a=\frac{r_\mathrm{Z}+r_\mathrm{M}}{2}.\] Za \(r_\mathrm{M}\) dosadíme vztah (1): \[ a=\frac{r_\mathrm{Z}+r_\mathrm{Z}\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}}{2}.\] Vytkneme \(r_\mathrm{Z}\): \[ a=\frac{r_\mathrm{Z}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right]}{2}.\tag{4}\]
Číselné řešení:
\[ a=\frac{149{,}6{\cdot}10^6\left[1+\sqrt[3]{\left(\frac{686{,}96}{365{,}25}\right)^2}\right]} {2} \mathrm{km} \dot = 188{,}8{\cdot}10^6 \mathrm{km}.\]
c) Doba letu kosmické lodi ze Země na Mars po Hohmannově trajektorii
Dobu letu kosmické lodi označíme t. Doba celého obletu po Hohmannově elipse je tedy 2t.
Dle třetího Keplerova zákona bude platit: \[\left(\frac{2t}{T_\mathrm{Z}}\right)^2=\left(\frac{a}{r_\mathrm{Z}}\right)^3.\] Obě strany rovnice vynásobíme \(T_\mathrm{Z}^2\): \[\left(2t \right)^2 =T_\mathrm{Z}^2\left(\frac{a}{r_\mathrm{Z}}\right)^3.\] Obě strany rovnice odmocníme: \[ 2t =T_\mathrm{Z}\sqrt{\left(\frac{a}{r_\mathrm{Z}}\right)^3}.\] Obě strany rovnice vydělíme dvěma: \[ t =\frac{T_\mathrm{Z}}{2}\sqrt{\left(\frac{a} {r_\mathrm{Z}}\right)^3}.\] Za \(a\) dosadíme vztah (4): \[ t =\frac{T_\mathrm{Z}}{2}\sqrt{\left(\frac{\frac{r_\mathrm{Z}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right]}{2}} {r_\mathrm{Z}}\right)^3}.\] Vykrátíme \(r_\mathrm{Z}\) a zlomek upravíme: \[ t =\frac{T_\mathrm{Z}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right] ^3 }.\tag{5}\]
Číselné řešení:
\[ t =\frac{365{,}25}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{,}96}{365{,}25}\right)^2}\right]^3} \mathrm{dne} \dot= 258{,}86 \mathrm{dne} .\]
d) Poloha Marsu \(M_{1}\) v okamžiku startu kosmické lodi
Určíme, o jaký úhel \(\alpha_\mathrm{M}\) se Mars za dobu od startu rakety do jejího přistání posunul po své dráze.
Sestavíme trojčlenku: \[T_\mathrm{M} ..... 2\pi\] \[t ..... \alpha_\mathrm{M}.\] Jedná se o přímou úměrnost, bude tedy platit: \[\frac{t}{T_\mathrm{M}}=\frac{\alpha_\mathrm{M}}{2\pi}.\] Vyjádříme \(\alpha_\mathrm{M}\) tak, že obě strany rovnice vynásobíme \(2\pi\): \[\alpha_\mathrm{M}=2\pi\frac{t}{T_\mathrm{M}}.\] Za \(t\) dosadíme (5): \[\alpha_{M}=2\pi\frac{ \frac{T_{Z}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right] ^3 }}{T_\mathrm{M}}.\]
Číselné řešení:
Úhlu \(2\pi\) odpovídá ve stupňové míře úhel \(360\mathrm{°}.\) Při výpočtu budeme pracovat ve stupňové míře: \[\alpha_\mathrm{M}=360\frac{\frac{365{,}25}{2}\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{,}96}{365{,}25}\right)^2}\right]^3}}{686{,}96}\mathrm{°} \dot= 136\mathrm{°}.\]
Poloha Země \(Z_{2}\) v okamžiku jejího přistání
Určíme, o jaký úhel \(\alpha_\mathrm{Z}\) se Země za dobu od startu rakety do jejího přistání posunula po své dráze.
Sestavíme trojčlenku: \[T_\mathrm{Z} ..... 2\pi\] \[t ..... \alpha_\mathrm{Z}.\] Jedná se o přímou úměrnost, bude tedy platit: \[\frac{t}{T_\mathrm{Z}}=\frac{\alpha_\mathrm{Z}}{2\pi}.\] Vyjádříme \(\alpha_\mathrm{Z}\) tak, že obě strany rovnice vynásobíme \(2\pi\): \[\alpha_\mathrm{Z}=2\pi\frac{t}{T_\mathrm{Z}}.\] Za \(t\) dosadíme (5): \[\alpha_\mathrm{Z}=2\pi\frac{ \frac{T_\mathrm{Z}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right] ^3 }}{T_{Z}}.\] Vykrátíme \(2T_\mathrm{Z}\): \[\alpha_\mathrm{Z}=\pi \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right] ^3 }.\]
Číselné řešení:
Úhlu \(\pi\) odpovídá ve stupňové míře úhel \(180\mathrm{°}.\) Při výpočtu budeme pracovat ve stupňové míře: \[\alpha_\mathrm{Z}=180\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{686{,}96}{365{,}25}\right)^2}\right]^3}\mathrm{°} \dot= 255\mathrm{°}.\]
Polohu Marsu \(M_{1}\) v okamžiku startu kosmické lodi a polohu Země \(Z_{2}\) v okamžiku jejího přistání zakreslíme do obrázku.
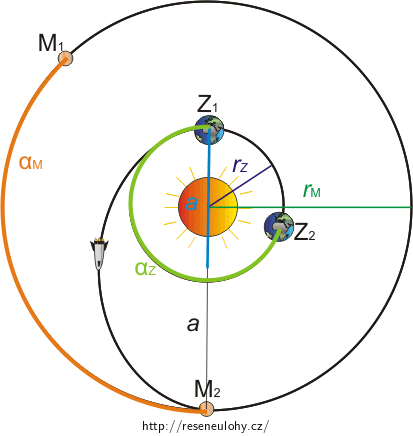
Odpověď
a) Poloměr trajektorie Marsu je roven: \(r_\mathrm{M}=r_\mathrm{Z}\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\) a velikost jeho rychlosti: \(v=\frac{2\pi r_\mathrm{Z}\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}}{T_\mathrm{M}}\).
Pro zadané hodnoty dostáváme: \(r_\mathrm{M}=227{,}94{\cdot}10^6 \mathrm{km}\) a \(v\dot=24{,}13 \mathrm{\frac{km}{s}}\).
b) Délka velké poloosy Hohmannovy trajektorie je rovna: \( a=\frac{r_\mathrm{Z}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right]}{2}\).
Pro zadané hodnoty dostáváme: \( a \dot = 188{,}8{\cdot}10^6 \mathrm{km}\).
c) Doba letu kosmické lodi ze Země na Mars po Hohmannově trajektorii je rovna: \( t =\frac{T_\mathrm{Z}}{2} \sqrt { \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right] ^3 }\).
Pro zadané hodnoty dostáváme: \( t \dot= 258{,}86 \mathrm{dne} .\)
d) Mars se při svém pohybu posunul o úhel: \(\alpha_\mathrm{M}=2\pi\frac{ \frac{T_\mathrm{Z}}{2} \sqrt {\frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right]^3}}{T_\mathrm{M}}\).
Pro zadané hodnoty dostáváme: \(\alpha_\mathrm{M} \dot= 136\mathrm{°}\).
Země se při svém pohybu posunula o úhel: \(\alpha_\mathrm{Z}=\pi\sqrt{ \frac{1}{8}\left[1+\sqrt[3]{\left(\frac{T_\mathrm{M}}{T_\mathrm{Z}}\right)^2}\right]^3}\) .
Pro zadané hodnoty dostáváme: \(\alpha_\mathrm{Z} \dot= 255\mathrm{°}\).




