Sbírka řešených úloh

Ocelová kulička

Úloha číslo: 110

• Zápis

  a = 0,5 m·s−2	zrychlení kuličky
  s =  20 m	celková dráha kuličky
  t = 12 s	celková doba pohybu kuličky
  t1 = ? (s)	doba pohybu kuličky po nakloněné rovině

• Nápověda 1: Dráha a rychlost kuličky na nakloněné rovině

  Nakreslete si obrázek situace a označte potřebné veličiny.

  Jakou dráhu urazí kulička po nakloněné rovině a jaké rychlosti při tom dosáhne?

• Řešení k nápovědě 1

  Obrázek:

  

  Kulička se po nakloněné rovině pohybuje rovnoměrně zrychleným přímočarým pohybem a na vodorovné rovině pohybem rovnoměrným přímočarým. Na nakloněné rovině se kulička pohybuje po dobu t₁ s daným zrychlením a. Za tento čas ujede dráhu

  \[s_1\,=\,\frac{1}{2}\,at_1^{2}\,\]

  a dosáhne rychlosti

  \[v\,=\,at_1\,.\]

• Nápověda 2: Pohyb kuličky po vodorovné dráze

  Jakým pohybem se pohybuje kulička po vodorovné části dráhy?

  Jakou má při tom rychlost?

  Jakou dráhu urazí?

• Řešení k nápovědě 2

  Po vodorovné části dráhy se kulička pohybuje pohybem rovnoměrným přímočarým.

  Pohybuje se rychlostí, kterou dosáhla při pohybu na nakloněné rovině, tedy v.

  Touto rychlostí se pohybuje po vodorovné rovině po dobu t − t₁ a ujede dráhu s₂:

  \[s_2\,=\,v(t\,-\,t_1)\,=\,at_1(t-t_1)\,.\]

• Nápověda 3: Celková dráha kuličky

  Vyjádřete celkovou dráhu, kterou kulička urazila.

  Řešte získanou kvadratickou rovnici pro hledaný čas t₁ a zvažte, který kořen vyhovuje podmínkám úlohy.

• Řešení k nápovědě 3

  Celková dráha bude:

  \[s\,=\,\frac{1}{2}\,at_1^{2}\,+\,at_1\left(t\,-\,t_1\right)\,.\]

  Po roznásobení závorky:

  \[s\,=\,-\frac{1}{2}\,at_1^{2}\,+\,at_1t\,.\]

  A po úpravě:

  \[t_1^{2}\,-\,2tt_1\,+\,\frac{2s}{a}\,=\,0\,.\]

  Řešením kvadratické rovnice dostaneme dva kořeny (ozn. t₁, t₂), z nichž vyhovuje pouze:

  \[t_1\,=\,t\,-\,\sqrt{t^{2}\,-\,\frac{2s}{a}}\,.\]

  Protože:

  \[t_1\,<\,t\,.\]

  Číselně:

  \[t_1\,=\,\left(12\,-\,\sqrt{(12)^{2}\,-\,\frac{2{\cdot} 20}{0{,}5}}\right) \,\mathrm{s} \,=\, 4\,\mathrm{s}\,.\]

• CELKOVÉ ŘEŠENÍ

  Obrázek a označení veličin:

  

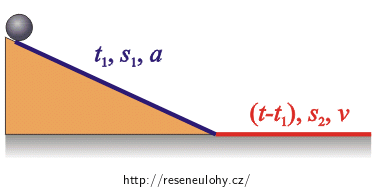
  Kulička se po nakloněné rovině pohybuje rovnoměrně zrychleným přímočarým pohybem a na vodorovné rovině pohybem rovnoměrným přímočarým. Na nakloněné rovině se kulička pohybuje po dobu t₁ s daným zrychlením a. Za tento čas ujede dráhu:

  \[s_1\,=\,\frac{1}{2}at_1^{2}\,.\]

  A dosáhne rychlosti:

  \[v\,=\,at_1\,.\]

  Touto rychlostí se pohybuje po vodorovné rovině po dobu t − t₁ a ujede dráhu:

  \[s_2\,=\,v\left(t-t_1\right)\,=\,at_1\left(t-t_1\right)\,.\]

  Celková dráha bude:

  \[s\,=\,\frac{1}{2}\,at_1^{2}\,+\,at_1\left(t-t_1\right)\,.\]

  Po roznásobení závorky:

  \[s\,=\,-\frac{1}{2}\,at_1^{2}\,+\,at_1t\,.\]

  A po úpravě:

  \[t_1^{2}\,-\,2tt_1\,+\,\frac{2s}{a}\,=\,0\,.\]

  Řešením kvadratické rovnice dostaneme dva kořeny (ozn. t₁, t₂), z nichž vyhovuje pouze:

  \[t_1\,=\,t\,-\,\sqrt{t^{2}\,-\,\frac{2s}{a}}\,.\]

  Protože:

  \[t_1\,<\,t\,.\]

  Číselně:

  \[t_1\,=\,\left(12\,-\,\sqrt{(12)^{2}\,-\,\frac{2{\cdot} 20}{0{,}5}}\right)\,\mathrm{s}\,=\,4\,\mathrm{s}\,.\]

• Odpověď

  Ocelová kulička se pohybuje po nakloněné rovině po dobu:

  \[t_1\,=\,t\,-\,\sqrt{t^{2}\,-\,\frac{2s}{a}}\,=\, 4\,\mathrm{s}\,.\]