Těžiště neobvyklého kruhu
Úloha číslo: 1128
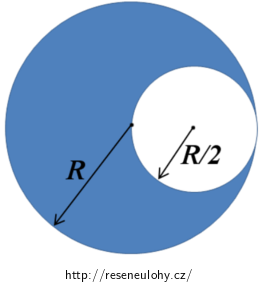
Určete polohu těžiště plošného útvaru znázorněného na obrázku níže.
Nápověda 1
Zamyslete se nad tím, co vlastně znamená úkol „určete polohu těžiště“. Co má být výstupem úlohy, co vlastně určujete?
Nápověda 2
Vhodně umístěte útvar do souřadného systému. Lze jeho polohu zvolit tak, aby se další výpočty zjednodušily, event. některé nebylo třeba vůbec dělat?
Popis metody
Polohový vektor rT popisující polohu těžiště obvykle počítáme pomocí integrálu:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\]Tvar tohoto zkoumaného objektu je ovšem netypický a získat x-ovou souřadnici těžiště integrací je – jemně řečeno – nesmírně obtížné. Níže se proto pokusíme daný problém vyřešit jiným způsobem (omezujeme se na rovinný problém). Pomohou nám dva různé pohledy na stejný celek:
Situace 1: Na chvíli si představíme, že do našeho útvaru doplníme zpátky vyříznutý malý kruh. Těžiště T1 doplněného velkého kruhu o hmotnosti m bude ležet v jeho středu, jeho souřadnice tedy bude xT1 = R.
Situace 2: Nyní si plný kruh opět rozdělíme na:
- „vykousnutý“ útvar o hmotnosti m1, jehož těžiště má hledanou souřadnici xT,
- malý kruh o hmotnosti m2, jehož těžiště T2 má souřadnici xT2 = 3R/2.
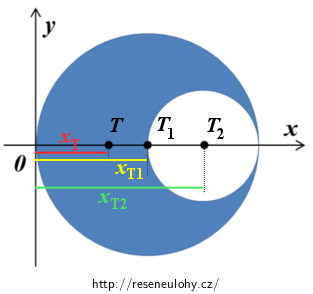
Protože jsme tentýž zkoumaný objekt popsali jednou jako celek, jednou jako systém dvou částí, je jasné, že těžiště soustavy „vykousnutý“ útvar + malý kruh musí být v místě těžiště celého plného kruhu. Tato myšlenka pro nás bude východiskem při dalších výpočtech.
Nápověda 3
Myšlenku uvedenou tučně v předcházející části „Popis metody“ převeďte do matematického vyjádření. Dosaďte známé souřadnice xT1 a xT2 a vyjádřete neznámou xT.
Nápověda 4
Pomocí plošné hustoty dopočtěte hmotnosti m1 a m2. Předpokládejte, že útvar je homogenní a jeho plošná hustota ρ je tedy všude stejná.
Nápověda 5
Dosaďte hmotnosti ze vztahů (5) a (6) do vztahu (4) a vyjádřete hledanou souřadnici xT.
Celkové řešení
Určit polohu těžiště znamená určit souřadnice těžiště v nějakém vhodně zvoleném souřadném systému. Protože daný útvar je rovinný (třetí rozměr, „výšku“, zanedbáváme), jsou výstupem úlohy dvě souřadnice těžiště T: xT, yT. Výhodné umístění útvaru do souřadného systému ukazuje obrázek níže – levý okraj útvaru prochází počátkem soustavy souřadnic.
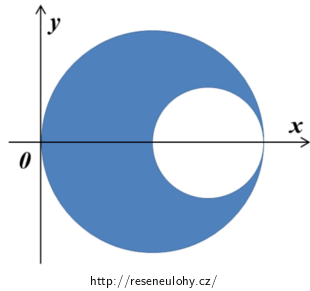
Protože takto umístěný útvar je osově symetrický podle osy x, musí jeho těžiště ležet na této ose – libovolný bod na ose x má ovšem nulovou y-ovou souřadnici, tedy ihned můžeme psát:
\[y_\mathrm{T}\,=\,0.\]Dále tedy stačí vypočítat pouze x-ovou souřadnici těžiště xT. Tento výpočet obvykle provádíme pomocí integrálu:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dm}{{\int}dm},\]kde rT je polohový vektor popisující polohu těžiště. Tvar tohoto zkoumaného objektu je ovšem netypický a získat x-ovou souřadnici těžiště integrací je – jemně řečeno – nesmírně obtížné. Níže se proto pokusíme daný problém vyřešit jiným způsobem (omezujeme se na rovinný problém). Pomohou nám dva různé pohledy na stejný celek:
Situace 1: Na chvíli si představíme, že do našeho útvaru doplníme zpátky vyříznutý malý kruh. Těžiště T1 doplněného velkého kruhu o hmotnosti m bude ležet v jeho středu, jeho souřadnice tedy bude xT1 = R.
Situace 2: Nyní si plný kruh opět rozdělíme na:
- „vykousnutý“ útvar o hmotnosti m1, jehož těžiště má hledanou souřadnici xT ,
- malý kruh o hmotnosti m2, jehož těžiště T2 má souřadnici xT2 = 3R/2.

Protože jsme tentýž zkoumaný objekt popsali jednou jako celek, jednou jako systém dvou částí, je jasné, že těžiště soustavy „vykousnutý“ útvar + malý kruh musí být v místě těžiště celého plného kruhu. Této myšlence lze dát následující matematickou podobu:
\[x_\mathrm{T1}\,=\,\frac{m_1x_\mathrm{T}\,+\,m_2x_\mathrm{T2}}{m_1\,+\,m_2},\tag{1}\]kde pravá strana rovnice vychází ze vzorce pro výpočet polohy těžiště soustavy hmotných bodů či těles – podrobněji například v úloze Těžiště různě uspořádaných soustav koulí.
Protože známe souřadnice xT1 a xT2, můžeme za ně do vztahu (1) dosadit a vyjádřit xT:
\[R\,=\,\frac{m_1x_\mathrm{T}\,+\,m_2{\cdot}\frac{3R}{2}}{m_1\,+\,m_2},\tag{2}\] \[R(m_1\,+\,m_2)\,-\,m_2\frac{3R}{2}\,=\,m_1x_\mathrm{T},\tag{3}\] \[x_\mathrm{T}\,=\,R(1\,-\,\frac{m_2}{2m_1}).\tag{4}\]Hmotnost malého kruhu m2 určíme jako součin obsahu malého kruhu a plošné hustoty:
\[m_2\,=\,{\pi}\frac{R^2}{4}\varrho.\tag{5}\]Hmotnost m1 „vykousnutého“ útvaru můžeme určit jako rozdíl hmotnosti m celého velkého kruhu a hmotnosti m2 malého kruhu:
\[m_1\,=\,m\,-\,m_2\,=\,{\pi}R^2\varrho\,-\,{\pi}\frac{R^2}{4}\varrho\,=\,\frac{3}{4}{\pi}R^2\varrho.\tag{6}\]Na závěr dosadíme ze vztahů (5) a (6) do vztahu (4):
\[x_\mathrm{T}\,=\,R(1\,-\,\frac{m_2}{2m_1})\,=\,R(1\,-\,\frac{{\pi}\frac{R^2}{4}\varrho}{2{\cdot}\frac{3}{4}{\pi}R^2\varrho})\,=\,\frac{5}{6}R.\tag{7}\]Souřadnice těžiště „vykousnutého“ útvaru xT je tedy rovna 5R/6.
Alternativní řešení
Jiná metoda řešení je postavená na znalosti práce s momenty sil. Využívá poznatku, že máme-li (v rovině) soustavu hmotných bodů či plošných útvarů podrobenou silám, můžeme vzhledem k libovolnému bodu roviny určit momenty těchto sil. Tyto síly mají dohromady na soustavu stejný otáčivý účinek jako jejich výslednice s působištěm v těžišti soustavy. Určíme tedy nejdříve momenty jednotlivých sil:
Určení momentu tíhové síly – útvar považujeme za celek:
Působiště tíhové síly FG je v těžišti T zkoumaného útvaru – rameno tíhové síly je tedy rovno hledané veličině xT (viz obrázek):
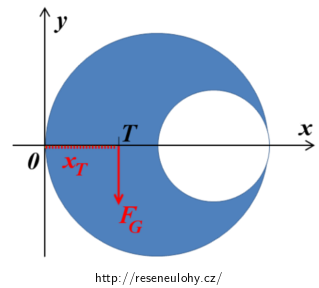
Pro velikost momentu tíhové síly FG vzhledem k počátku souřadného systému tedy platí:
\[M_1\,=\,F_Gx_\mathrm{T}\,=\,mgx_\mathrm{T}\,=\,{\varrho}Sgx_\mathrm{T},\tag{8}\]kde ρ je plošná hustota útvaru, S jeho plošný obsah a g tíhové zrychlení.
Z geometrických vlastností obrazce můžeme jeho obsah určit jako:
\[S\,=\,{\pi}R^2\,-\,{\pi}(\frac{R}{2})^2\,=\,\frac{3}{4}{\pi}R^2.\tag{9}\]Dosazením ze vztahu (9) do vztahu (8) dostáváme:
\[M_1\,=\,\frac{3}{4}{\pi}R^2{\varrho}g{\cdot}x_T.\tag{10}\]Určení momentů sil – útvar rozložíme na dvě části:
Nyní budeme uvažovat velký kruh bez jakýchkoli vyříznutí. Na takový kruh působí síla FG1, jejíž působiště je ve středu velkého kruhu, a pro velikost momentu tíhové síly FG1 vzhledem k počátku soustavy souřadnic tedy platí:
\[M_2\,=\,F_\mathrm{G1}R.\] Protože doplněním velkého kruhu o vyřízlou část jsme zvětšili jeho hmotnost, budeme nyní uvažovat, že malý kruh má efektivní hmotnost zápornou – tak dostaneme výslednou hmotnost útvaru. (Jako by vykrojený malý kruh nadlehčoval velký plný kruh.) Efektivní tíhová síla na malý kruh FG2 bude tedy směřovat svisle vzhůru a její působiště bude ve středu malého kruhu. Pro velikost momentu tíhové síly FG2 vzhledem k počátku soustavy souřadnic pak platí: \[M_3\,=\,F_\mathrm{G2}{\cdot}\frac{3R}{2}.\]Ramena sil lze snadno odečíst z obrázku:
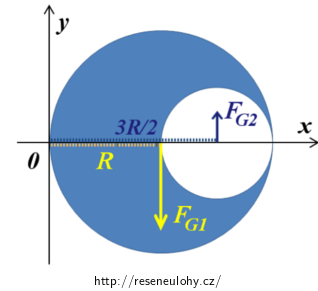
Výsledný moment sil FG1 a FG2 získáme jako rozdíl dílčích momentů (rozdíl proto, že síly mají opačné otáčivé účinky). Pro velikost výsledného momentu M tedy platí:
\[M\,=\,M_2\,-\,M_3\,=\,R(F_\mathrm{G1}\,-\,\frac{3}{2}F_\mathrm{G2}).\tag{11}\]Vztah (11) nyní upravíme pomocí plošné hustoty ρ podobně jako vztah (1):
\[M\,=\,Rg(m_1\,-\,\frac{3}{2}m_2)\,=\,Rg{\varrho}(S_1\,-\,\frac{3}{2}S_2),\tag{12}\]kde S1 je obsah velkého kruhu a S2 obsah malého kruhu. S přihlédnutím ke geometrii útvaru lze psát:
\[M\,=\,Rg{\varrho}({\pi}R^2\,-\,\frac{3}{2}{\pi}({\frac{R}{2}})^2)\,=\,\frac{5}{8}R^3g{\varrho}{\pi}.\tag{13}\]Porovnání výše vypočítaných momentů:
Podle základní úvahy našeho postupu platí:
\[M_1\,=\,M.\tag{14}\]Dosadíme do rovnosti (14) ze vztahů (10) a (13) a vyjádříme xT:
\[\frac{3}{4}{\pi}R^2{\varrho}g{\cdot}x_\mathrm{T}\,=\,\frac{5}{8}R^3g{\varrho}{\pi},\] \[\frac{3}{4}x_T\,=\,\frac{5}{8}R,\] \[x_\mathrm{T}\,=\,\frac{20}{24}R\,=\,\frac{5}{6}R.\]Souřadnice těžiště xT je rovna 5R/6.
Odpověď
Souřadnice těžiště zadaného útvaru v námi zvoleném souřadném systému jsou:
\[x_\mathrm{T}\,=\,\frac{5}{6}R,\] \[y_\mathrm{T}\,=\,0.\]




