Rotor turbíny
Úloha číslo: 208
Rotor turbíny se otáčel rychlostí 3000 otáček za minutu. Pak ho začali brzdit tak, že se otáčky rovnoměrně snižovaly. Rotor se zastavil za 2 min. Kolik otáček vykonal rotor od počátku brzdění až do svého zastavení?
Zápis
f0 = 3000 min−1 = 50 s−1 počáteční frekvence T = 2 min = 120 s doba brzdění n = ? počet otáček Nápověda 1 – řešení úvahou
Rozmyslete si, jak lze pro určení počtu otáček využít fakt, že klesají rovnoměrně.
Nápověda 2 – grafické řešení
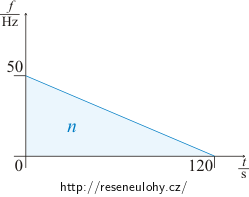
Nakreslete graf závislosti frekvence otáčení kola na čase. Kde je v grafu schovaný daný počet otáček?
Nápověda 3 – řešení integrací
Napište matematicky, jak závisí počet otáček rotoru na čase. Jak pomocí této závislosti určíte celkový počet otáček v daném časovém intervalu?
Celkové řešení
1. způsob řešení – úvahou:
Protože se frekvence otáčení snižuje rovnoměrně, můžeme určit průměrnou frekvenci jako aritmetický průměr krajních hodnot. Frekvence klesla z počátečních 3000 otáček za minutu na nulu během dvou minut. Aritmetický průměr tedy je 1500 otáček za minutu.
Můžeme si představit, že s touto průměrnou frekvencí se rotor otáčí po celé dvě minuty, tedy celkový počet vykonaných otáček je 3000.
2. způsob řešení – graficky:
Graf závislosti frekvence na čase:
Počtu otáček odpovídá plocha pod křivkou:
\[n\,=\,\frac{f_{0}T}{2}.\]Číselně:
\[n\,=\, \frac{50{\cdot}120}{2}\,=\, 3000.\]3. způsob řešení – integrací:
Frekvence otáčení se s časem mění podle vztahu:
\[f\left(t\right)\,=\, f_{0} - kt,\]kde
\[\{k\}\,=\,\frac{50}{120} = \frac{5}{12}\](směrnice přímky v grafu z Nápovědy 2).
Počet otáček rotoru od začátku brzdění do zastavení pak můžeme spočítat jako integrál funkce f(t) v daném časovém intervalu (obsah plochy pod křivkou):
\[n\,=\,\int_{0}^{T}{f(t)}\mathrm{d}t\,=\, \int_{0}^{T}{(f_{0} - kt)}\mathrm{d}t,\] \[n\,=\,\left[f_{0}t - \frac{kt^{2}}{2}\right]_{0}^{T}\,=\, f_{0}T - k\frac{T^{2}}{2}.\]Číselně:
\[n\,=\, 50{\cdot}120 \,-\, \frac{5}{12}\frac{120^{2}}{2}\,=\, 3000.\]Odpověď
Počet otáček:
\(n\,=\,\frac{f_{0}T}{2} = 3000\,.\)Rotor vykonal 3000 otáček.
Podobná úloha
Zkuste podobnou úlohu Otáčení kola.