Potopí se. Nebo ne?
Úloha číslo: 1033
Dřevěná tyč o průřezu 1 cm2 a délce 1,5 m je zatížena železným závažím o hmotnosti 40 g a je ponořena ve svislé poloze do dostatečně hlubokého rybníka s vodou.
- Určete, zda tyč se závažím klesne na dno rybníka.
- Pokud neklesne, určete, jaká část tyče bude vyčnívat nad hladinu.
Hustota dřeva tyče je 600 kg·m-3, hustota železa 7800 kg·m-3.
Zápis
S = 1 cm2 = 1·10-4 m2 obsah plochy průřezu tyče l = 1,5 m délka tyče m = 40 g hmotnost závaží ρD = 600 kg·m−3 hustota dřeva ρZ = 7800 kg·m−3 hustota železa x = ? délka části tyče vyčnívající nad hladinu Nápověda 1
Nakreslete si obrázek, který situaci zachycuje. Jaké síly na soustavu tyče a závaží působí? Co by pro ně muselo platit, aby soustava klesla ke dnu?
Nápověda 2
Napište podmínky, které musí síly splňovat, aby:
- se soustava zcela ponořila,
- zůstala část tyče vynořená.
Která z uvedených sil v závislosti na ponoření tyče mění svoji velikost a rozhodne tedy, který případ nastane?
Nápověda 3
Ve vztahu (1) jste schopni s pomocí definice hustoty a vztahu pro objem válce určit všechny síly, přímo tedy umíme rozhodnout, zda nerovnost platí, či ne. Udělejte to!
Nápověda 4
Zbývá dopočítat, jak velká část tyče bude vyčnívat nad hladinu. Již jsme zjistili, že s výjimkou jediné se působící síly nezmění. Využijte tedy předešlých výpočtů a s pomocí vztahu (2) určete délku vynoření tyče x.
Celkové řešení
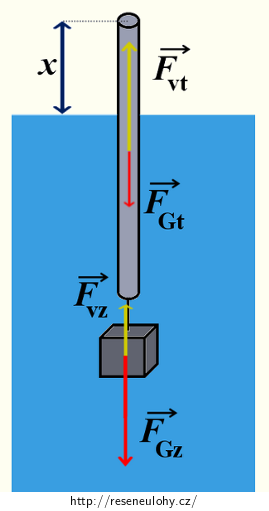
Na soustavu působí směrem svisle dolů tyto dvě síly:
- tíhová síla na závaží FGz,
- tíhová síla na tyč FGt.
Na soustavu působí směrem svisle nahoru tyto dvě síly:
- vztlaková síla na závaží Fvz,
- tíhová síla na tyč Fvt.
a. Aby se soustava zcela ponořila, musí být součet sil působících směrem dolů větší než součet sil působících vzhůru:
\[F_\mathrm{Gz}\,+\,F_\mathrm{Gt}\,>\,F_\mathrm{vz}\,+\,F'_\mathrm{vt}\,.\tag{1}\]Zde F´vt je vztlaková síla působící na zcela ponořenou tyč (pod vodou je celý objem tyče).
b. Pokud zůstane část tyče vynořená nad hladinou (a tedy v klidu), ustaví se rovnováha sil:
\[F_\mathrm{Gz}\,+\,F_\mathrm{Gt}\,=\,F_\mathrm{vz}\,+\,F''_\mathrm{vt}\,.\tag{2}\]Zde F´´vt je vztlaková síla působící na částečně ponořenou tyč (pod vodou je jen část objemu tyče).
(Poznámka: Mezním případem je pak situace, kdy nastane rovnost sil, ale celý objem tyče je ponořen – plování.)
Jediná síla, která mění svoji velikost v závislosti na ponoření, je vztlaková síla Fvt působící na tyč.
Postupně dopočítáme velikosti jednotlivých sil ze vztahu (1) a posoudíme platnost této nerovnosti:
\[F_\mathrm{Gz}\,=\,mg\,=\,0{,}040{\cdot}9{,}81\,\mathrm{N}\,\dot=\,0{,}39\,\mathrm{N}\,.\](Zde m je hmotnost závaží a g tíhové zrychlení.)
\[F_\mathrm{Gt}\,=\,m_\mathrm{t}g\,={\rho}_\mathrm{D}V_\mathrm{t}g\,=\,{\rho}_\mathrm{D}Slg\,=\,600{\cdot}1{\cdot}10^{-4}{\cdot}1{,}5{\cdot}9{,}81\,\mathrm{N}\,\\\dot=\,0{,}88\,\mathrm{N}\](Zde mt je hmotnost tyče, kterou určujeme jako součin hustoty tyče ρD a jejího objemu Vt; objem Vt je vzhledem k válcovému tvaru tyče dopočítán jako součin obsahu podstavy S a délky tyče l; g je tíhové zrychlení.)
\[F_\mathrm{vz}\,=\,{\rho}V_\mathrm{z}g\,=\,{\rho}\frac{m}{\rho_\mathrm{Z}}g\,=\,1000{\cdot}\frac{0{,}040}{7800}{\cdot}9{,}81\,\mathrm{N}\,\dot=\,0{,}05\,\mathrm{N}\](Zde ρ je hustota vody, Vz objem ponořeného závaží, který určíme jako podíl hmotnosti závaží m a jeho hustoty ρZ; g je tíhové zrychlení.)
\[F'_\mathrm{vt}\,=\,{\rho}V_\mathrm{t}g\,=\,{\rho}Slg\,=\,1000{\cdot}1{\cdot}10^{-4}{\cdot}1{,}5{\cdot}9{,}81\,\mathrm{N}\,\dot=\,1{,}47\,\mathrm{N}\](Zde ρ je hustota vody, Vt objem celé ponořené tyče, který vzhledem k válcovému tvaru tyče určíme jako součin obsahu podstavy S a délky tyče l; g je tíhové zrychlení.)
Po dosazení do nerovnosti (1) dostáváme:
\[(0{,}39\,+\,0{,}88)\,\mathrm{N}\,>\,(0{,}05\,+\,1{,}47)\,\mathrm{N}\,,\] \[1{,}27\,\mathrm{N}\,>\,1{,}52\,\mathrm{N}\,.\]Tato nerovnost zjevně neplatí, soustava závaží–tyč se tedy zcela ponořit nemůže – vztlaková síla působící na tyč by byla příliš velká.
Předchozích výpočtů využijeme nyní k tomu, abychom určili, jaká část tyče zůstane vynořena nad hladinou. Síly FGz, FGt i Fvz se nezměnily, je třeba znovu vyjádřit pouze vztlakovou sílu (nyní již značenou F´´vt) odpovídající pouze ponořené části tyče o délce l−x:
\[F''_\mathrm{vt}\,=\,{\rho}V_\mathrm{t}'g\,,\tag{3}\]kde ρ je hustota vody, Vt objem ponořené části tyče a g tíhové zrychlení. Objem ponořené části tyče zaujímá tvar válce a můžeme jej tedy určit jako:
\[V_\mathrm{t}'\,=\,S(l\,-\,x)\,.\tag{4}\]Ze vztahu (4) dosadíme do vztahu (3):
\[F''_\mathrm{vt}\,=\,{\rho}S(l\,-\,x)g\,.\tag{5}\]Současně lze ale sílu F´´vt vyjádřit ze vztahu (2):
\[F''_\mathrm{vt}\,=\,F_\mathrm{Gz}\,+\,F_\mathrm{Gt}\,-\,F_\mathrm{vz}\,.\tag{6}\]Porováním vztahů (5) a (6) dostáváme:
\[F_\mathrm{Gz}\,+\,F_\mathrm{Gt}\,-\,F_\mathrm{vz}\,=\,{\rho}S(l\,-\,x)g\,,\] \[x\,=\,l\,-\,\frac{F_\mathrm{Gz}\,+\,F_\mathrm{Gt}\,-\,F_\mathrm{vz}}{{\rho}Sg}\,.\]Číselně:
\[x\,\dot=\,(1{,}5\,-\,\frac{0{,}39\,+\,0{,}88\,-\,0{,}05}{1000{\cdot}1{\cdot}10^{-4}{\cdot}9{,}81})\,\mathrm{m}\,\dot=\,26\,\mathrm{cm}\,.\]Alternativní řešení
Jiný postup vypadá tak, že začnete počítat délku vyčnívající tyče x, aniž byste provedli ověření, že se celá soustava neponoří na dno. Samotný výsledek vám totiž napoví, zda se tak stane, či nikoliv.
Hledaná délka x té části tyče, která zůstane nad hladinou, je totiž jistě veličina, která nabývá kladných hodnot. Čím víc se bude tato hodnota blížit nule, tím méně bude tyč vyčnívat nad hladinu.
Pro x = 0 m je tyč zcela ponořena a plove ve vodě tak, že její horní okraj se zespoda dotýká hladiny.
Jakmile bychom získali hodnotu x zápornou, lze tento výsledek přirozeně fyzikálně interpretovat tak, že závaží i s tyčí se ponořilo na dno rybníka.
Můžete se tedy přímo pustit do výpočtu x a na základě znaménka získaného výsledku pak zpětně odpovědět také na první otázku.
Odpověď
Soustava závaží+tyč se na dno rybníka nepotopí, nad hladinou zůstane přibližně 26 cm dlouhá část tyče.




