Náraz střely na konec otočné tyče

Úloha číslo: 489

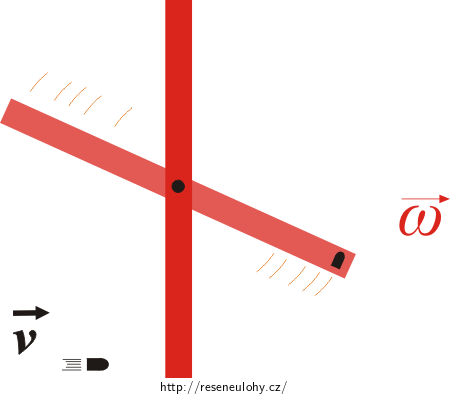
Dřevěná tyč délky 40 cm a hmotnosti 1 kg se může otáčet kolem osy kolmé na tyč a procházející jejím středem. Na konec tyče narazí střela o hmotnosti 10 g a rychlosti 200 m·s^-1 ve směru kolmém na osu i na tyč. Určete úhlovou rychlost, kterou se tyč dá do pohybu, když v ní střela uvázne.

Poznámka: Předpokládáme, že střela se do tyče nejprve velmi rychle zaryje a pak se dá celá soustava do pohybu hledanou úhlovou rychlostí.

Zápis

d = 40 cm	délka tyče
M = 1 kg	hmotnost tyče
m = 10 g	hmotnost střely
v₁ = 200 m·s⁻¹	rychlost střely
ω = ? (s⁻¹)	rychlost otáčení tyče

Teorie – vektorový součin
Vektorovým součinem vektorů \(\vec{a}\times \vec{b}\) rozumíme operaci, která dané dvojici přiřadí vektor \(\vec{c}\), pro nějž bude platit:
- \(\vec{c} = \vec{n} |\vec{a}||\vec{b}| sin \varphi\),
- \(\vec{a}\vec{b}\vec{c}\) tvoří pravotočivou bázi,
kde \( \vec{n}\) je jednotkový vektor kolmý na \(\vec{a}\) i \(\vec{b}\) a φ je úhel, který vektory \(\vec{a}\) a \(\vec{b}\) svírají.

Zda trojice vektorů \(\vec{a}\vec{b}\vec{c}\), kde \(\vec{c}\) je kolmý na dva zbylé, tvoří pravotočivou bázi, zjistíme podle pravidla pravé ruky. Pokud prsty pravé ruky ukazují směr nejkratší cesty, kterou by se na sebe přenesly \(\vec{a}\) a \(\vec{b}\), pak zdvižený palec ukazuje směr vektoru \(\vec{c}\). Není-li tato podmínka splněna, jedná se o bázi levotočivou.

Zvláště důležité jsou tedy případy:
- φ = 0 (vektory jsou rovnoběžné) → \(\vec{a}\times \vec{b} = 0,\)
- φ = π/2 nebo 3π/2 (vektory jsou kolmé) → \(\vec{a}\times \vec{b} = \vec{n} |\vec{a}||\vec{b}|,\)
\[\vec{a}\times \vec{b} = \vec{c},\] \[\vec{b}\times \vec{a} = -\vec{c},\] \[\vec{c}\times \vec{a} = \vec{b},\] \[\vec{c}\times \vec{b} = -\vec{a}.\]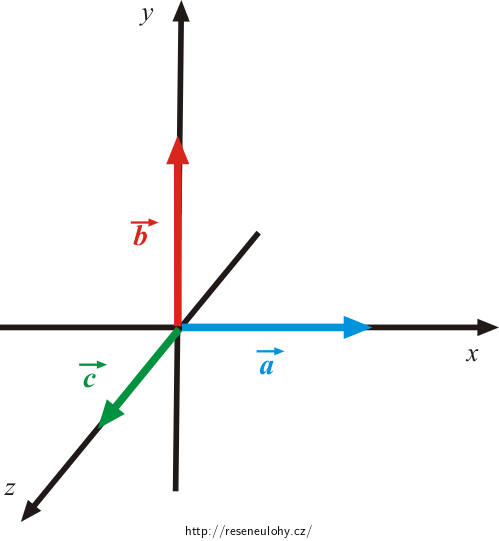
A tak dále...
Nápověda 1
Co musí platit pro soustavu tyč–střela těsně před a po nárazu střely do tyče? Nelze najít nějakou zachovávající se veličinu?
Řešení nápovědy 1
Je-li vzhledem k nějakému bodu soustavy moment vnějších sil na soustavu působící nulový, pak se celkový moment hybnosti vzhledem k uvažovanému bodu zachovává.

Uvedené větě se říká zákon zachování momentu hybnosti.

Budeme-li uvažovat soustavu tyč–střela ve dvou situacích — těsně před nárazem a těsně po nárazu střely — bude uvedená podmínka splněna.

Bude tedy platit:
\[\vec{L}_1 = \vec{L}_2,\]
kde

\(\vec{L}_1\) ... celkový moment hybnosti soustavy tyč–střela těsně před nárazem střely,

\(\vec{L}_2\) ... celkový moment hybnosti soustavy tyč–střela těsně po nárazu střely.
Nápověda 2
Jak je definován moment hybnosti? Zapište jeho definici pro hmotný bod a také vztah, který můžete použít v případě tuhého tělesa otáčejícího se okolo pevné osy.

Zapište i příslušné velikosti vektoru momentu hybnosti a uvědomte si, kam vektor míří.
Řešení nápovědy 2
Moment hybnosti hmotného bodu \(\vec{L}\) vzhledem k bodu S je definován jako vektorový součin polohového vektoru a hybnosti hmotného bodu:
\[\vec{L} = \vec{r} \times \vec{p}\,.\]
Pro velikost vektorového součinu platí:
\[L = rp\sin\varphi \,,\]
kde φ je úhel sevřený oběma vektory.

Vektor momentu hybnosti je kolmý k rovině určené vektory \(\vec{r}\) a \(\vec{p}\). Jeho orientaci lze určit pravidlem pravé ruky: prsty dáme tak, aby směřovaly od \(\vec{r}\) k \(\vec{p}\), napnutý palec pak ukazuje směr vektoru \(\vec{L}\).

Pro moment hybnosti tuhého tělesa vzhledem k pevné ose otáčení platí:
\[\vec{L} = J\vec{\omega}\,,\]
kde J je moment setrvačnosti tělesa vzhledem k pevné ose otáčení a \(\vec{\omega}\) úhlová rychlost otáčení.

Pro velikost momentu hybnosti platí:
\[L = J\omega\,.\]
Směr vektoru momentu hybnosti je daný směrem vektoru úhlové rychlosti \(\vec{\omega}\).
Nápověda 3
Zapište, čemu je roven moment hybnosti soustavy tyč–střela těsně před zásahem a těsně po zásahu. Zjistěte, jaký má směr, a napište i příslušné velikosti momentu hybnosti v obou situacích.
Řešení nápovědy 3
Situace (1) — těsně před nárazem střely:

Tyč je v této situaci v klidu, celkový moment hybnosti je tedy roven momentu hybnosti střely.

Moment hybnosti střely vzhledem k ose otáčení:
\[\vec{L}_1 = \vec{r} \times \vec{p}\,.\]
Vektor míří kolmo k obrazovce (papíru) a je orientován směrem před ni:

Pro velikost platí:
\[L_1 = rp\sin\varphi \,,\]
kde φ je rovno 90° a r je rovno d/2:
\[L_1 = pr = mvr = \frac{1}{2}mdv.\tag{1}\]
Situace (2) — těsně po nárazu střely:

Střela je již zaryta do tyče a začíná se spolu s ní otáčet. Pro moment hybnosti můžeme psát:
\[\vec{L}_2 = J\vec{\omega}\,,\]
kde J je moment setrvačnosti tyče plus střely vzhledem k ose otáčení procházející středem tyče a \(\vec{\omega}\) hledaná úhlová rychlost otáčení.

Pro velikost momentu hybnosti platí:
\[L = J\omega\,.\]
Směr vektoru momentu hybnosti je daný směrem vektoru úhlové rychlosti a míří kolmo k tyči, stejně jako osa otáčení, orientován je směrem před obrazovku (papír), tedy stejně jako \(\vec{L}_1.\)

Momenty setrvačnosti tenké tyče otáčející se kolem svého středu a moment setrvačnosti hmotného bodu otáčejícího se po kružnici o průměru d (jím nahradíme střelu) jsou:
\[J_\mathrm{tyc} = \frac{1}{12}Md^2\,,\] \[J_\mathrm{strela} = mr^2 = m\left(\frac{d}{2}\right)^2 = \frac{1}{4}md^2\,.\]
Odtud pro velikost momentu setrvačnosti ve druhé situaci:
\[L_2 = \omega(J_\mathrm{tyc} + J_\mathrm{strela})\,,\] \[L_2= \omega d^2(\frac{1}{12}M + \frac{1}{4}m)\,.\tag{2}\]
Nápověda 4
K vyjádření hledané úhlové rychlosti využijte zákon zachování momentu hybnosti.
Řešení nápovědy 4
Ze zákona zachování momentu hybnosti dostáváme:
\[\vec{L}_1 = \vec{L}_2\,.\]
Rovnost platí i pro velikosti momentů hybnosti:
\[L_1 = L_2.\]
Dosadíme ze vztahů (1) a (2):
\[\frac{1}{2}mdv = \omega d^2(\frac{1}{12}M + \frac{1}{4}m)\,.\]
Odtud dostáváme:
\[\omega = \frac{mv}{d(\frac{1}{6}M+\frac{1}{2}m)}\,,\]
\[\omega = \frac{0{,}01 {\cdot} 200}{0{,}4 \cdot (\frac{1}{6} \cdot 1+\frac{1}{2} \cdot 0{,}01)} \mathrm{s}^{-1} = 29{,}1 \mathrm{s}^{-1}.\]
Celkové řešení

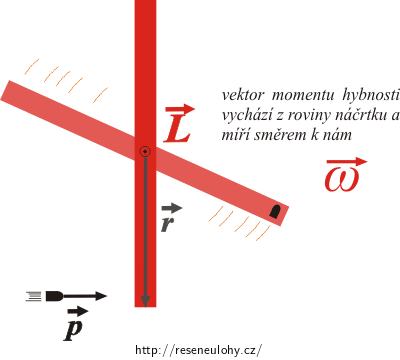
Při řešení úlohy vyjdeme ze zákona zachování momentu hybnosti. Budeme zkoumat situaci (1), těsně před nárazem střely, tj. v momentě, od kterého bude mít trajektorie střely už tvar kružnice, a situaci (2), těsně po nárazu střely, kdy už se střela dává do pohybu spolu s tyčí.

Ze zákona zachování momentu hybnosti dostáváme:
\[\vec{L}_1 = \vec{L}_2\,,\]
kde

\(\vec{L}_1\) ... celkový moment hybnosti soustavy tyč–střela těsně před nárazem střely,

\(\vec{L}_2\) ... celkový moment hybnosti soustavy tyč–střela těsně po nárazu střely.

Situace (1) — těsně před nárazem střely:

Tyč je v této situaci v klidu, celkový moment hybnosti je tedy roven momentu hybnosti střely.

Moment hybnosti střely vzhledem k ose otáčení je roven:
\[\vec{L}_1 = \vec{r} \times \vec{p}\,.\]
Vektor míří kolmo k obrazovce (papíru) a je orientován směrem před ni:

Pro velikost platí:
\[L_1 = rp\sin\varphi \,,\]
kde φ je rovno 90° a r je rovno d/2:
\[L_1 = pr = mvr = \frac{1}{2}mdv.\tag{1}\]
Situace (2) — těsně po nárazu střely:

Střela je již zaryta do tyče a začíná se spolu s ní otáčet. Pro moment hybnosti můžeme psát:
\[\vec{L}_2 = J\vec{\omega}\,,\]
kde J je moment setrvačnosti tyče plus střely vzhledem k ose otáčení procházející středem tyče a \(\vec{\omega}\) je hledaná úhlová rychlost otáčení.

Pro velikost momentu hybnosti platí:
\[L = J\omega\,.\]
Směr vektoru momentu hybnosti je daný směrem vektoru úhlové rychlosti a míří kolmo k tyči, stejně jako osa otáčení, orientován je směrem před obrazovku (papír), tedy stejně jako \(\vec{L}_1.\)

Momenty setrvačnosti tenké tyče otáčející se kolem svého středu a moment setrvačnosti hmotného bodu otáčejícího se po kružnici o průměru d (jím nahradíme střelu) jsou:
\[J_\mathrm{tyc} = \frac{1}{12}Md^2\,,\] \[J_\mathrm{strela} = mr^2 = m\left(\frac{d}{2}\right)^2 = \frac{1}{4}md^2\,.\]
Odtud pro velikost momentu setrvačnosti ve druhé situaci:
\[L_2 = \omega(J_\mathrm{tyc} + J_\mathrm{strela})\,,\] \[L_2= \omega d^2(\frac{1}{12}M + \frac{1}{4}m)\,.\tag{2}\]
Ze zákona zachování momentu hybnosti dostáváme:
\[\vec{L}_1 = \vec{L}_2\,.\]
Rovnost platí i pro velikosti momentů hybnosti:
\[L_1 = L_2\,.\]
Dosadíme ze vztahů (1) a (2):
\[\frac{1}{2}mdv = \omega d^2(\frac{1}{12}M + \frac{1}{4}m)\,.\]
Odtud dostáváme:
\[\omega = \frac{mv}{d(\frac{1}{6}M+\frac{1}{2}m)}\,,\]
\[\omega = \frac{0{,}01 {\cdot} 200}{0{,}4 \cdot (\frac{1}{6} \cdot 1+\frac{1}{2} \cdot 0{,}01)} \mathrm{s}^{-1} = 29{,}1 \mathrm{s}^{-1}\,.\]
Odpověď
Úhlovou rychlost tyče po nárazu střely vypočítáme ze vztahu:
\[\omega = \frac{mv}{d(\frac{1}{6}M+\frac{1}{2}m)}\,.\]
Číselný výsledek: ω = 29,1 s^-1.
Proč neřešit přes energie?
Pro situace (1) a (2) nemůžeme použít zákon zachování mechanické energie, protože v průběhu zarývání střely dochází k deformaci a zahřátí střely i tyče – nepůsobí zde jen konzervativní síly.