Plovoucí kužel
Úloha číslo: 1032
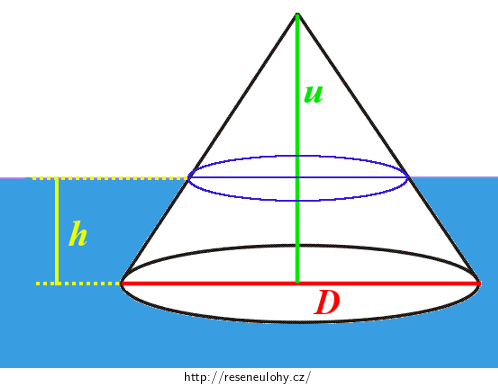
Rotační kužel s průměrem podstavy 20 cm a výškou 30 cm je vyroben z materiálu, který má hustotu 800 kg·m-3. Určete, do jaké výšky bude ponořen, plove-li ve vodě špičkou vzhůru.
Zápis
D = 20 cm = 0,20 m průměr podstavy kužele u = 30 cm = 0,30 m výška kužele ρT = 800 kg·m−3 hustota materiálu, ze kterého je kužel vyroben h = ? výška, do které je kužel ponořen Nápověda 1
Rozmyslete si, jaké síly na kužel plovoucí na vodě působí? Jaký je jejich směr a jaká jejich výslednice? (Uplatněte 1. Newtonův zákon.)
Nápověda 2 – určení tíhové síly
Budete muset vypočítat velikost tíhové a vztlakové síly působící na kužel.
Nejprve zkuste určit tíhovou sílu působící na kužel. Při dosazování do dobře známého vztahu pro její výpočet potřebujete znát hmotnost kužele – jaké veličiny vám k tomu poskytuje zadání? Využijte definiční vztah pro hustotu a připomeňte si, jak se počítá objem kužele.
Nápověda 3 – určení vztlakové síly
Určete vztlakovou sílu působící na kužel. Kterou z potřebných veličin zatím stále neznáte?
Nápověda 4 – určení vztlakové síly
Navrhněte způsob, jak vypočítat objem ponořené části kužele. Možných postupů je víc. Jistě ale budete potřebovat znát průměr d podstavy takového kužele, který vznikne, když si z původního kužele odmyslíte ponořenou část. Nakreslete si řez původního kužele svislou rovinou a k určení průměru d si připomeňte podobnost trojúhelníků.
Nápověda 5
Dosaďte do vztahu pro vztlakovou sílu a položte ji do rovnosti s tíhovou silou podle vztahu (1). Vyjádřete a číselně dopočítejte veličinu h.
Komentář
Povšimněte si, že výška kužele, která je ponořená, nezávisí na rozměru podstavy kužele, ale pouze na jeho výšce.
Poznámka
Objem ponořené části V0 jsme počítali jako rozdíl objemu celého kužele a vynořené části. Stejně tak by jej bylo možné určit jako objem komolého kužele s podstavami o průměrech D a d.
Celkové řešení
Na kužel působí:
- tíhová síla FG směrem svisle dolů,
- vztlaková síla Fvz směrem svisle vzhůru.
Protože kužel je vzhledem k pozorovateli v klidu, je podle 1. Newtonova zákona výslednice sil na něj působících nulová:
\[\vec{F}_\mathrm{G}\,+\,\vec{F}_\mathrm{vz}\,=\,\vec{o}\,.\]Protože působící síly mají opačný směr, lze pro jejich velikosti psát:
\[F_\mathrm{G}\,-\,F_\mathrm{vz}\,=\,0\,\Rightarrow\,F_\mathrm{G}\,=\,F_\mathrm{vz}\,.\tag{1}\]
Tíhovou sílu spočítáme dle důvěrně známého vztahu:
\[F_\mathrm{G}\,=\,mg\,,\tag{2}\]kde g je tíhové zrychlení a m hmotnost kužele – tu ovšem neznáme. Zadána je ale hustota materiálu, ze kterého je kužel vyroben, a některé rozměry. Vyjádříme tedy hmotnost z definičního vztahu pro hustotu:
\[{\rho}_\mathrm{T}\,=\,\frac{m}{V}\,\Rightarrow\,m\,=\,V{\rho}_\mathrm{T}\,,\tag{3}\]kde ρT je hustota materiálu kužele a V jeho objem. Dosazením vztahu (3) do rovnice (2) dostáváme:
\[F_\mathrm{G}\,=\,V{\rho}_\mathrm{T}g\,.\tag{4}\]Také rovnice (4) obsahuje stále ještě veličinu, kterou neznáme – objem V rotačního kužele. Objem se určí jako jedna třetina ze součinu obsahu podstavy a výšky kužele, tedy v našem případě:
\[V\,=\,\frac{1}{3}{\pi}(\frac{D}{2})^2u\,,\tag{5}\]kde D a u jsou výše zadané rozměry kužele. Dosazením vztahu (5) do (4) dostáváme finální výraz pro tíhovou sílu:
\[F_\mathrm{G}\,=\,\frac{1}{12}{\pi}D^2u{\rho}_\mathrm{T}g\,.\tag{6}\]
Také vztlakovou sílu vypočítáme podle známého vztahu:
\[F_\mathrm{vz}\,=\,V_0{\rho}g\,,\tag{7}\]kde V0 je objem ponořené části kužele, ρ hustota kapaliny (tj. v našem případě vody) a g tíhové zrychlení. První z těchto veličin zatím neznáme.
Jednoduchý způsob, jak určit objem ponořené části kužele, je odečíst od celkového objemu kužele V objem V´ jeho vynořené části:
\[V_0\,=\,V\,-\,V'\,.\tag{8}\]Celkový objem V jsme již spočítali ve vztahu (5), nyní tedy potřebujeme určit objem vynořené části kužele V´. Tato část má opět tvar kužele a opět tedy pro její výpočet potřebujeme znát výšku (označme ji v) a obsah podstavy (označme jej Sp):
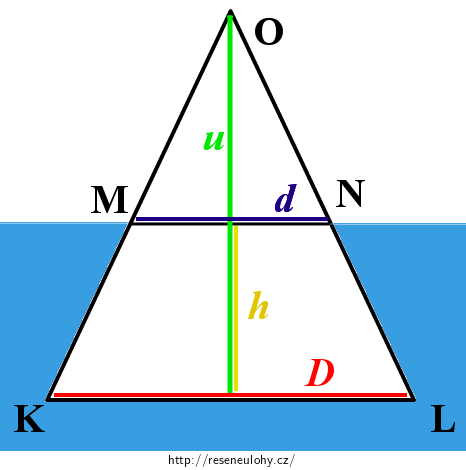
\[V'\,=\,\frac{1}{3}S_\mathrm{p}v\,.\tag{9}\]Pro snadnější určení těchto dvou veličin si nakreslíme celý kužel v řezu.
Snadno odtud vidíme, že:
\[v\,=\,u\,-\,h\,.\tag{10}\]Pro určení obsahu podstavy potřebujeme znát její průměr d (nebo poloměr d/2). Z obrázku je patrné, že trojúhelníky KLO a MNO jsou si podobné, tedy platí:
\[\frac{D}{d}\,=\,\frac{u}{u-h}\,\Rightarrow\,d\,=\,\frac{D(u\,-\,h)}{u}\,.\tag{11}\]Nyní dosadíme ze vztahů (10) a (11) do vztahu (9):
\[V'\,=\,\frac{1}{3}S_\mathrm{p}v\,=\,\frac{1}{3}{\pi}(\frac{d}{2})^2v\,=\,\frac{1}{12}{\pi}(\frac{D(u\,-\,h)}{u})^2(u\,-\,h)\,.\tag{12}\]Konečně ze vztahů (12) a (5) dosadíme do vztahu (8) a získáme objem ponořené části kužele:
\[V_0\,=\,\frac{1}{3}{\pi}(\frac{D}{2})^2u\,-\,\frac{1}{12}{\pi}(\frac{D(u\,-\,h)}{u})^2(u\,-\,h)\\\,=\,\frac{1}{12}{\pi}D^2(u\,-\frac{(u\,-\,h)^3}{u^2})\,.\tag{13}\]Dosazením (13) do vztahu (7) určíme vztlakovou sílu jako:
\[F_\mathrm{vz}\,=\,\frac{1}{12}{\pi}D^2(u\,-\,\frac{(u\,-\,h)^3}{u^2}){\rho}g\,.\tag{14}\]
Dle (1) položíme nyní tíhovou sílu (vztah (6)) a vztlakovou sílu (vztah (14)) do rovnosti a vyjádříme h:
\[F_\mathrm{G}\,=\,F_\mathrm{vz}\,,\] \[\frac{1}{12}{\pi}D^2u{\rho}_Tg\,=\,\frac{1}{12}{\pi}D^2(u\,-\,\frac{(u\,-\,h)^3}{u^2}){\rho}g\,,\] \[u{\rho}_T\,=\,(u\,-\,\frac{(u\,-\,h)^3}{u^2}){\rho}\,,\] \[u^3{\rho}_T\,=\,u^3{\rho}\,-\,(u\,-\,h)^3{\rho}\,,\] \[(u\,-\,h)^3\,=\,\frac{u^3({\rho}\,-\,{\rho}_T)}{\rho}\,,\] \[u\,-\,h\,=\,u\sqrt[3]{\frac{{\rho}\,-\,{\rho}_T}{\rho}}\,,\] \[h\,=\,u(1\,-\,\sqrt[3]{\frac{{\rho}\,-\,{\rho}_T}{\rho}})\,.\] Číselně: \[h\,=\,0{,}30{\cdot}(1\,-\,\sqrt[3]{\frac{1000\,-\,800}{1000}})\,\mathrm{m}\,\dot=\,12{,}5\,\mathrm{cm}\,.\]Odpověď
Výška ponořené části kužele bude přibližně 12,5 cm.