Vozík
Úloha číslo: 148
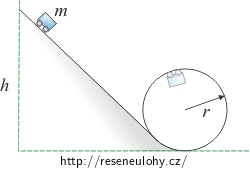
Malý vozík o hmotnosti m sjíždí bez smýkání po dráze zakončené válcovou plochou o poloměru r. Z jaké výšky h musí vozík sjíždět, aby projel celou kruhovou smyčku této válcové plochy? Moment setrvačnosti a valivý odpor koleček zanedbejte.
Zápis
m hmotnost vozíku r poloměr válcové plochy h = ? výška, z níž musí vozík sjíždět, aby projel celou kruhovou smyčku válcové plochy Rozbor
Aby vozík projel celou dráhu, musí mít v nejvyšším bodě smyčky nenulovou rychlost. Nejprve zjistíme, jaká je minimální hodnota této rychlosti. K tomu využijeme 2. Newtonův zákon. Vozík sjíždí bez smýkání, takže k nalezení výšky použijeme zákon zachování mechanické energie.
Nápověda 1 - rychlost v nejvyšším bodě kruhové smyčky
Zjistěte, jakou minimální rychlost musí mít vozík v nejvyšším bodě smyčky, aby ještě projel dráhu. Nakreslete si obrázek, vyznačte do něj síly působící na vozík a napište pro něj pohybovou rovnici. Jaká bude velikost působících sil v kritickém okamžiku, kdy vozík začne odpadat?
Nápověda 2 - zákon zachování mechanické energie
Zvolte si hladinu nulové potenciální energie. Napište, jaká je mechanická energie vozíku v okamžiku, kdy ho vypouštíme (1), a v nejvyšším bodě smyčky (2).
Celkové řešení
Aby vozík projel celou dráhu, musí mít v nejvyšším bodě smyčky nenulovou rychlost. Nejprve zjistíme, jaká je minimální hodnota této rychlosti. K tomu využijeme 2. Newtonův zákon. Vozík sjíždí bez smýkání, takže k nalezení výšky použijeme zákon zachování mechanické energie.
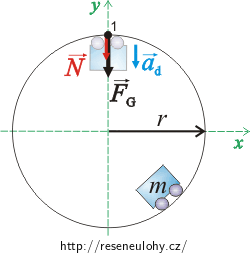
V nejvyšším bodě působí na vozík tíhová síla \(\vec{F_\mathrm{G}}\) a normálová síla \(\vec{N}\), kterou působí kruhová smyčka na vozík. Zrychlení vozíku \(\vec{a_\mathrm{d}}\) směřuje dolů ke středu kruhové smyčky.
\[\vec{N}+\vec{F_\mathrm{G}}\,=\,m\vec{a_\mathrm{d}}\]\(N\)…normálová síla, kterou kruhová smyčka působí na vozík
\(F_\mathrm{G}\)…tíhová síla působící na vozík
\(a_\mathrm{d}\)…normálové zrychlení vozíku
Zvolíme souřadný systém podle obrázku a přepíšeme pohybovou rovnici skalárně:
\[-N-F_\mathrm{G}\,=\,-ma_\mathrm{d},\] \[N+mg\,=\,ma_\mathrm{d},\]\(m\)…hmotnost vozíku,
\(g\)…tíhové zrychlení.
V okamžiku, kdy vozík začne odpadat, přestane na něj smyčka tlačit a síla N bude nulová. Minimální rychlost, kterou musí vozík jet, aby se udržel na dráze a nespadl, dostaneme z podmínky, že N = 0 N.
\[mg\,=\,ma_\mathrm{d}\] \[mg\,=\,m\frac{v_1^2}{r}\]\(v_1\)…rychlost v nejvyšším bodě kruhové smyčky
\(r\)…poloměr kruhové smyčky
Odtud si vyjádříme rychlost v1:
\[g\,=\,\frac{v_1^2}{r},\] \[v_1\,=\,\sqrt {gr}.\tag{1}\]K určení hledané výšky využijeme zákon zachování mechanické energie. Zvolíme hladinu nulové potenciální energie a napíšeme, jaká je celková mechanická energie vozíku v okamžiku, kdy ho vypouštíme (1), a v nejvyšším bodě smyčky (2).
\[\mathrm{ZZME:} \hspace{15px} E_\mathrm{p1}\,=\,E_\mathrm{p2}+E_\mathrm{k2}\]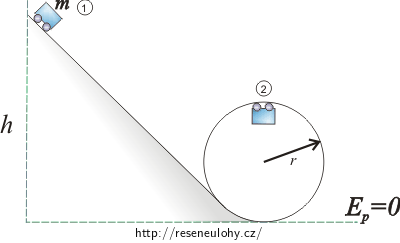
\(E_\mathrm{p1}\)…potenciální energie vozíku ve výšce h
\(E_\mathrm{p2}\)…potenciální energie vozíku v nejvyšším bodě smyčky
\(E_\mathrm{k2}\)…kinetická energie vozíku v nejvyšším bodě smyčky
\[mgh \,=\, mg2r + \frac{1}{2}mv_1^2\]Za rychlost v1 dosadíme ze vztahu (1):
\[mgh \,=\, mg2r + \frac{1}{2}mgr,\] \[h\,=\,\frac{5r}{2}.\]Odpověď: Výška, ze které musí vozík sjíždět, se rovná \(h\,=\,\frac{5r}{2}\).
Odpověď
Výška, ze které musí vozík sjíždět, se rovná \(h\,=\,\frac{5r}{2}.\)




