Skrýš pro oříšek
Úloha číslo: 1215
Poblíž stromu, na kterém bydlí veverka, se nachází tunel, který prochází středem Země. Veverka se rozhodla, že do něj schová oříšek o hmotnosti \(m\).

Poznámka: Předpokládejte, že v tunelu je vzduchoprázdno a Země je homogenní koule. Zanedbejte rotaci Země.
Nápověda a1)
S využitím Newtonova gravitačního zákona vyjádřete gravitační sílu, která působí na oříšek ve vzdálenosti \(r\) od středu Země.
Nápověda a2)
Dle rovnice (5) určete, jaký pohyb bude oříšek konat.
Nápověda a3)
Znáte výslednou sílu působící na oříšek. Napište pro něj druhý Newtonův zákon.
Nápověda a4)
Řešte diferenciální rovnici (7). Najděte její charakteristický polynom a fundamentální systém. Promyslete si, jaké byly počáteční podmínky, a zjistěte, čemu se rovná \(r\).
Nápověda a5)
Jaký fyzikální význam má výraz \(\sqrt{\frac{\kappa M}{R^3}}\) ve vztahu (13)?
Nápověda b)
Znáte vztah pro závislost polohového vektoru oříšku na čase. Určete s jeho pomocí závislost rychlosti oříšku na čase.
Poté zjistěte, jakou dobu bude oříšku trvat, než se dostane do středu Země, a jaká rychlost odpovídá této době. Dopočítejte číselné řešení.
Nápověda c)
Oříšek koná harmonický pohyb, proto se vrátí. Čas, který mu to zabere, odpovídá jedné periodě \(T\). Dopočítejte ji číselně.
Celkové řešení
a) Pohyb a pohybová rovnice oříšku
Formulujeme Newtonův gravitační zákon pro gravitační sílu, která působí na oříšek ve vzdálenosti \(r\) od středu Země.
Nakreslíme si obrázek Země s oříškem, kde \(R\) je poloměr Země, \(r\) je vzdálenost oříšku od středu Země, \(m\) je hmotnost oříšku a \(M_\mathrm{r}\) je hmotnost části Země, která leží uvnitř koule o poloměru \(r\).
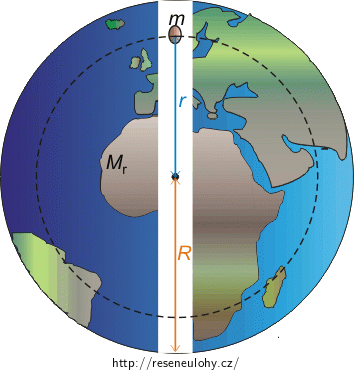
Na oříšek působí síla, která je vyvolána částí Země o hmotnosti \(M_\mathrm{r}\). Výsledné silové působení zbylé části Země je nulové.
Napíšeme si vztah pro \(M_\mathrm{r}\): \[M_\mathrm{r}=\rho V_\mathrm{r},\tag{1}\] kde \(\rho\) je předpokládaná hustota homogenní Země a \(V_\mathrm{r}\) je objem, který je ohraničen přerušovanou čarou v obrázku Země s oříškem. Pro objem \(V_\mathrm{r}\) platí vztah: \[V_\mathrm{r}=\frac{4\pi r^3}{3}.\tag{2}\] Do vztahu (1) dosadíme (2): \[M_\mathrm{r}=\rho \frac{4\pi r^3}{3}.\tag{3}\]
Gravitační síla, která působí na oříšek ve vzdálenosti \(r\) od středu Země, bude vypadat následovně: \[F=-\kappa \frac{mM_\mathrm{r}}{r^2},\tag{4}\] kde \(\kappa\) je gravitační konstanta. Do vztahu (4) dosadíme (3): \[F=-\kappa \frac{m\rho \frac{4\pi r^3}{3}}{r^2}.\] Vykrátíme \(r^2\) a zlomek upravíme: \[F=-\kappa \frac{m\rho 4\pi r}{3}.\tag{5}\]
Pohyb oříšku
Ve vztahu (5) označíme konstanty písmenem \(k=\kappa \frac{m\rho 4\pi }{3}\): \[F=-kr.\] Vzniklý vztah se podobá vztahu pro sílu pružnosti v Hookově zákoně. Oříšek se chová jako harmonický oscilátor a koná harmonický pohyb.
Druhý Newtonův zákon
Známe výslednou sílu působící na oříšek. Napíšeme pro něj druhý Newtonův zákon: \[F=ma,\] kde \(a\) je zrychlení oříšku.
Zrychlení vyjádříme jako druhou derivaci vzdálenosti oříšku od středu Země \(r\) podle času \(t\): \[F=m \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\tag{6}\]
Dosadíme ze vztahu (5): \[-\kappa \frac{m\rho 4\pi r}{3}=m \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\] Obě strany rovnice vydělíme \(m\) a levou stranu vynásobíme jedničkou ve tvaru \(\frac{R^3}{R^3}\): \[-\kappa \frac{\rho 4\pi r}{3}\frac{R^3}{R^3}= \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\] \(\frac{\rho 4\pi}{3}{R^3}\) je hmotnost Země \(M\) a tedy: \[-\kappa \frac{Mr}{R^3}= \frac{\mathrm{d}^2r}{\mathrm{d}t^2}.\] Převedeme oba členy rovnice na jednu stranu: \[ \frac{\mathrm{d}^2r}{\mathrm{d}t^2}+\frac{\kappa M}{R^3}r=0.\tag{7}\]
Řešení diferenciální rovnice (7)
Určíme charakteristický polynom rovnice (7): \[ \lambda^2+\frac{\kappa M}{R^3}\lambda^0.\] Chceme najít jeho kořeny, proto ho položíme roven nule: \[ \lambda^2+\frac{\kappa M}{R^3}\lambda^0=0.\] Uvědomíme si, že \(\lambda^0=1\), a od obou stran rovnice odečteme člen \(\frac{\kappa M}{R^3}1\): \[ \lambda^2=-1\frac{\kappa M}{R^3}.\] Abychom mohli obě strany rovnice odmocnit, tak \(-1\) na pravé straně nahradíme druhou mocninou imaginární jednotky \(i^2\): \[ \lambda^2=i^2\frac{\kappa M}{R^3}.\] Obě strany rovnice odmocníme: \[ \lambda = ± i\sqrt{\frac{\kappa M}{R^3}}.\] Kořeny charakteristického polynomu jsou \(i\sqrt{\frac{\kappa M}{R^3}}\) a \(-i\sqrt{\frac{\kappa M}{R^3}}\).
Fundamentální systém je tedy \(e^{i\sqrt{\frac{\kappa M}{R^3}}t}\) a \(e^{-i\sqrt{\frac{\kappa M}{R^3}}t}\).
Řešení rovnice (7) hledáme ve tvaru: \[r=Ae^{i\sqrt{\frac{\kappa M}{R^3}}t}+Be^{-i\sqrt{\frac{\kappa M}{R^3}}t}.\tag{8}\]
Pro určení konstant \(A\) a \(B\) se podíváme na počáteční podmínky.
Ve chvíli, kdy veverka pustila oříšek do tunelu, byl čas roven nule \(t=0\), vzdálenost oříšku od středu Země byla rovna poloměru Země \(r=R\) a rychlost oříšku byla nulová \(v = \frac{\mathrm{d}r}{\mathrm{d}t}=0\).
Do vztahu (8) dosadíme \(t=0\) a \(r=R\): \[R=Ae^{i\sqrt{\frac{\kappa M}{R^3}}0}+Be^{-i\sqrt{\frac{\kappa M}{R^3}}0}.\] A protože \(e^0=1\): \[R=A+B.\tag{9}\]
Zderivujeme rovnici (8) podle času: \[\frac{\mathrm{d}r}{\mathrm{d}t}=i\sqrt{\frac{\kappa M}{R^3}}Ae^{i\sqrt{\frac{\kappa M}{R^3}}t}-i\sqrt{\frac{\kappa M}{R^3}}Be^{-i\sqrt{\frac{\kappa M}{R^3}}t}.\] Dosadíme \(t=0\) a \(\frac{\mathrm{d}r}{\mathrm{d}t}=0\): \[0=i\sqrt{\frac{\kappa M}{R^3}}Ae^0-i\sqrt{\frac{\kappa M}{R^3}}Be^0.\] \(e^0\) nahradíme \(1\) a obě strany rovnice vydělíme \(i\sqrt{\frac{\kappa M}{R^3}}\): \[0=A-B.\] K oběma stranám rovnice přičteme \(B\): \[A=B.\tag{10}\] Dosadíme vztah (10) do (9): \[R=B+B=2B.\] Obě strany rovnice vydělíme dvěma a vyjádříme \(B\): \[B=\frac{R}{2}.\] Dle (10) tedy platí: \[A=B=\frac{R}{2}.\tag{11}\] Dosadíme (11) do (8): \[r=\frac{R}{2}e^{i\sqrt{\frac{\kappa M}{R^3}}t}+\frac{R}{2}e^{-i\sqrt{\frac{\kappa M}{R^3}}t}.\tag{12}\]
Dále platí \(e^{iα}=\cos{α}+i\sin{α}\) a \(e^{-iα}=\cos{α}-i\sin{α}\). Rovnici (12) pak můžeme přepsat jako: \[r=\frac{R}{2}\cos{\sqrt{\frac{\kappa M}{R^3}}t}+i\frac{R}{2}\sin{\sqrt{\frac{\kappa M}{R^3}}t}+\frac{R}{2}\cos{\sqrt{\frac{\kappa M}{R^3}}t}-i\frac{R}{2}\sin{\sqrt{\frac{\kappa M}{R^3}}t}.\] Posčítáme siny a cosiny: \[r=R\cos{\sqrt{\frac{\kappa M}{R^3}}t}.\tag{13}\]
Fyzikální význam výrazu \(\sqrt{\frac{\kappa M}{R^3}}\) ve vztahu (13)
Jelikož oříšek koná harmonický pohyb, tak se jedná o úhlovou frekvenci \( ω\): \[ω=\sqrt{\frac{\kappa M}{R^3}}.\tag{14}\] Vztah (13) pak můžeme přepsat jako: \[r=R\cos{ωt}.\]
b) Rychlost oříšku ve středu Země
Závislost rychlosti oříšku na čase zjistíme derivací polohového vektoru.
Derivujeme (13): \[\begin{eqnarray}\frac{\mathrm{d}r}{\mathrm{d}t} &= &\frac{\mathrm{d}}{\mathrm{d}t}\left(R\cos{\sqrt{\frac{\kappa M}{R^3}}t}\right)\\ v &= &-R\sqrt{\frac{\kappa M}{R^3}}\sin{\sqrt{\frac{\kappa M}{R^3}}t}.\\ \end{eqnarray}\]
Oříšku bude trvat \(\frac{1}{4}\) jeho periody \(T\), než se dostane do středu Země: \[t=\frac{1}{4}T.\] Pro periodu platí vztah \(T=\frac{2 \pi}{ω}\), do kterého za \(ω\) dosadíme dle vztahu (14): \[T=2 \pi \sqrt{\frac{R^3}{\kappa M}}.\tag{15}\] Pro dobu \(t\) bude platit: \[t=\frac{1}{4}T=\frac{1}{4}2 \pi \sqrt{\frac{R^3}{\kappa M}}=\frac{\pi}{2}\sqrt{\frac{R^3}{\kappa M}}.\]
Dosadíme dobu \(t\) do vztahu pro rychlost a vztah upravíme (\({\sqrt{\frac{\kappa M}{R^3}}\sqrt{\frac{R^3}{\kappa M}}}=1\), \(sin{\frac{\pi}{2}}=1\), \(\frac{R^2}{R^3}=\frac{1}{R}\)): \[v=-R\sqrt{\frac{\kappa M}{R^3}}sin{\sqrt{\frac{\kappa M}{R^3}}\frac{\pi}{2}\sqrt{\frac{R^3}{\kappa M}}}=-\sqrt{\frac{\kappa MR^2}{R^3}}sin{\frac{\pi}{2}}=-\sqrt{\frac{\kappa M}{R}}. \]
Velikost rychlosti oříšku při průchodu středem Země je tedy rovna:
\[v = \sqrt{\frac{\kappa M}{R}}.\] V tabulkách dohledáme hodnoty pro \(R\), \(M\) a \(\kappa\).Poloměr Země \(R \dot= 6 378\cdot{10}^3 \mathrm{m}\) Hmotnost Země \(M \dot= 5{,}97\cdot{10}^{24} \mathrm{kg}\) Gravitační konstanta \(\kappa \dot= 6{,}67\cdot{10}^{-11} \mathrm{\frac{m^3}{kg\cdot s^{2}}}\) Dopočítáme velikost rychlosti číselně: \[v = \sqrt{\frac{6{,}67\cdot{10}^{-11}\cdot 5{,}97\cdot{10}^{24}}{6 378\cdot{10}^3} \mathrm{\frac{\frac{m^3}{kg\cdot s^{2}}\cdot kg}{m}}} \dot= 7 900 \mathrm{\frac{m}{s}} \dot= 28 440\mathrm{\frac{km}{h}}.\]
c) Návrat oříšku
Oříšek koná harmonický pohyb, proto se vrátí. Čas, který mu to zabere, odpovídá jedné periodě \(T\).
Využijeme vztahu pro periodu (15): \[T=2 \pi \sqrt{\frac{R^3}{\kappa M}}.\] V tabulkách dohledáme hodnoty pro \(R\), \(\kappa\), \(M\) a \(\pi\):
Oříšek se k veverce vrátí za dobu: \[T=2 {\cdot}3{,}14 \sqrt{\frac{\left(6378{\cdot} 10^3\right) ^3}{6{,}67\cdot{10}^{-11}\cdot 5{,}97\cdot{10}^{24}}\frac{\mathrm{m^3}}{\mathrm{\frac{m^3}{kg\cdot s^2}}\mathrm{kg}}} \dot= 5069 \mathrm{s} \dot= 84 \mathrm{min}\] \[T \dot= 1 \mathrm{h} 24 \mathrm{min}\]Poloměr Země \(R \dot= 6 378\cdot{10}^3 \mathrm{m}\) Gravitační konstanta \(\kappa \dot= 6{,}67\cdot{10}^{-11} \mathrm{\frac{m^3}{kg\cdot s^2}}\) Hmotnost Země \(M \dot= 5{,}97\cdot{10}^{24} \mathrm{kg}\) Ludolfovo číslo \(\pi \dot= 3{,}14\) Odpověď
a) Oříšek bude konat harmonický pohyb. Jeho pohybová rovnice je \( \frac{d^2r}{dt^2}+\frac{\kappa M}{R^3}r=0\). Přičemž \(r=R\cos{ωt}\), kde \(ω=\sqrt{\frac{\kappa M}{R^3}}\).
b) Rychlost oříšku při průletu středem Země je rovna \(v=-\sqrt{\frac{\kappa M}{R}} \) a číselná velikost rychlosti je \(v \dot= 28 440 \mathrm{\frac {km}{h}}. \)
c) Oříšek se vrátí k veverce za dobu \(T=2 \pi \sqrt{\frac{R^3}{\kappa M}}\), tedy přibližně za jednu hodinu a dvacet čtyři minut.




