Srážka puků na ledě
Úloha číslo: 1239
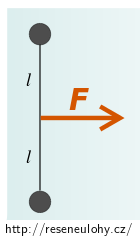
Na ledě leží dva hokejové puky spojené nehmotným vláknem délky \(2l\).
Na soustavu začne působit konstantní síla \(\vec{F}\), která je kolmá na spojnici puků a jejím působištěm je střed vlákna.
Jaká část mechanické energie se v okamžiku srážky puků přemění v energii vnitřní?
Předpokládejte, že se puky na ledě pohybují bez tření. Jejich srážku považujte za dokonale nepružnou.
Rozbor
Uvědomme si, že puky jsou identické a jejich vzdálenost \(l\) vůči působišti síly je stejná. Soustava je tedy symetrická vzhledem k vektorové přímce síly \(\vec F\). Můžeme tak v dalších výpočtech řešit pohyb pouze jednoho puku a výsledek pak rozšířit na puky oba.
Na oba puky působí tažná síla \(\vec F\) prostřednictvím vlákna, které chápeme pouze jako prostředníka této síly (nedeformuje se). Puky se začnou po zapojení síly pohybovat zrychleným pohybem, jak ve směru vektoru \(\vec{F}\), tak v linii jejich spojnice. Po určité době dojde k jejich srážce, jak plyne ze symetrie problému – na vektorové přímce síly \(\vec F\).
Protože uvažujeme, že srážka puků je dokonale nepružná, přemění se během ní kinetická energie odpovídající jejich rychlostem ve směru rázu těsně před srážkou na vnitřní energii dotčených těles. Po srážce k sobě zůstanou puky „přilepené“ a jejich pohyb bude pokračovat pouze ve směru síly \(\vec F\).
Kinetická energie puků příslušící rychlostem ve směru vektoru síly \(\vec{F}\) se se srážkou nezmění a dále poroste díky stálému urychlování tažnou sílou.
Puky byly na začátku v klidu. Nějaká síla je tedy musela urychlit. Pachateli jsou síly, kterými jsou puky prostřednictvím vlákna taženy. Pohybu ve směru spojnice puků přísluší složka síly v tomto směru, jejíž velikost však závisí na úhlu, který v daný moment vlákna svírají. Budeme-li znát průběh této síly, můžeme v tomto směru získanou a posléze ztracenou kinetickou energii vypočítat jako práci, kterou musela tato (proměnná) síla vykonat při přemístění puků ze vzdálenosti \(l\) do středu jejich spojnice.
Nápověda 1 – hledání velikosti tahových sil
Nakreslete si obrázek zachycující situaci několik okamžiků po začátku působení síly \(\vec F\). Pomocí vektorového rovnoběžníku rozložte sílu \(\vec F\) do směrů vláken.
Dokážete nalézt závislost velikosti tažných sil na velikosti úhlu \(\vartheta\), který v daném okamžiku svírají vlákna s osou symetrie?
Nápověda 2 – zavedení Oxy, rozklad tažné síly
Vhodně zaveďte soustavu souřadnic a určete složky vektoru tažné síly (např. \(\vec{T}_2\)).
Která složka síly \(\vec{T}_2\) je zodpovědná za urychlování soustavy ve směru \(\vec F\)? Která složka síly \(\vec{T}_2\) způsobuje urychlování v linii spojnice puků?
Vyjádřete složku vektoru \(\vec{T}_2\) ve směru osy \(y\).
Nápověda 3 – výpočet „ztracené“ energie
Při dokonale nepružné srážce se zachovává hybnost soustavy. Zkoumejte hybnost soustavy před a po srážce.
Vypočítejte kinetickou energii příslušící pohybu puku ve směru osy \(y\) v okamžiku těsně před srážkou.
Jak velká energie se při srážce přemění v energii vnitřní?
Celkové řešení
Obrázek vpravo zachycuje situaci soustavy v nějakém čase mezi uvedením do pohybu a srážkou.
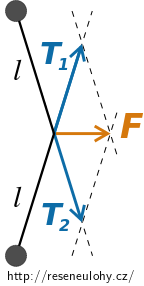
Sílu \(\vec{F}\) jsme rozložili do směrů vláken pomocí vektorového rovnoběžníku na síly \(\vec{T}_1\) a \(\vec{T}_2\), tj.
\[\vec{F} = \vec{T}_1 + \vec{T}_2.\]Než se pustíme do hledání závislosti velikosti tahových sil na velikosti úhlu, který vlákna svírají s osou symetrie, prozkoumejme následující geometrickou vlastnost.
Ze symetrie, která je dána tím, že síla \(\vec F\) působí uprostřed vlákna kolmo na spojnici obou puků, vychází skutečnost, že vektorový rovnoběžník je kosodelníkem a pro velikosti tahových sil platí
\[ |\vec{T}_1|=|\vec{T}_2| = T.\]Je tedy zřejmé, že postačí řešit úlohu pro jeden puk a v konečném výsledku zohlednit puky oba.
Nyní přejdeme k hledání závislosti velikosti tahové síly \(T\) na velikosti úhlu, který budeme značit \(\vartheta\) a je vyznačen v následujícím obrázku.
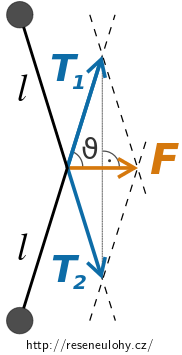
Protože je vektorový rovnoběžník kosodelníkem (jeho úhlopříčky se půlí), platí
\[\cos \vartheta = \frac{|\vec{F}|/2}{T} = \frac{F}{2T}.\]Závislost velikosti tažných sil \(T\) na úhlu \(\vartheta\) vyjádříme z předchozí rovnice vztahem
\[ T = \frac{F}{2\cos\vartheta}. \tag{1}\]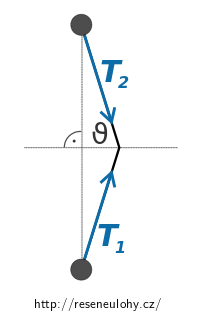
Na vlákna, která plní funkci tuhé vazby, působí síly \(\vec{T}_1\) a \(\vec{T}_2\). Síly, kterými jsou taženy puky, jsou představovány stejnými vektory \(\vec{T}_1\) a \(\vec{T}_2\). Pro usnadnění další úvahy si tyto vektory se zachováním orientace rovnoběžně posuneme tak, aby jejich působiště ležela ve středech puků (viz obr. vpravo).
Na základě geometrických vlastností má úhel vyznačený v obrázku stejnou velikost \(\vartheta\) jako uvažovaný úhel v rovnici (1). Při dalších rozkladech sil do význačných směrů budeme této skutečnosti využívat.
Zavedeme soustavu souřadnic \(\mathrm{Oxy}\) tak, že osa \(x\) leží v ose symetrie a je orientovaná ve směru vektoru \(\vec F\) a osa \(y\) míří kolmo vzhůru. Počátek ztotožníme s průsečíkem spojnice puků a osy symetrie.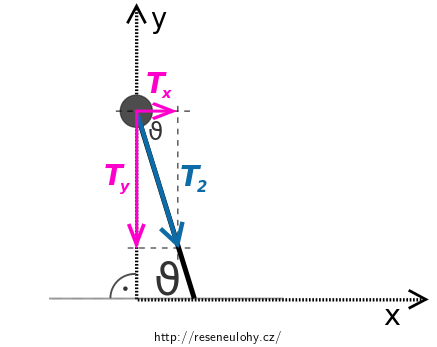
Sílu \(\vec{T}_2\) jsme rozložili do složek ve směru osy \(x\) (vektor \(\vec{T}_\mathrm{x}\)) a osy \(y\) (vektor \(\vec{T}_\mathrm{y}\)).
- Síla \(\vec{T}_\mathrm{x}\) puk urychluje ve směru osy \(x\).
- Síla \(\vec{T}_\mathrm{y}\) puk urychluje ve směru osy \(y\).
Velikost obou složek síly \(\vec{T}_2\), a tedy i okamžitá zrychlení v obou směrech závisí na velikosti úhlu \(\vartheta\).
Pro velikosti \(T_2\) a \(T_\mathrm{y}\) platí
\[\sin \vartheta = \frac{T_\mathrm{y}}{T_2} = \frac{T_\mathrm{y}}{T}.\]Pro složku vektoru \(\vec{T}_2\) ve směru osy \(y\) pak lze s pomocí předchozí rovnice psát
\[T_\mathrm{y} = -T\sin\vartheta.\] Dosazením vztahu (1) za T získáme \[T_\mathrm{y} = -\frac{F}{2\cos\vartheta}\sin\vartheta = -\frac{1}{2}F\,\mathrm{tg}\, \vartheta.\tag{2}\]Při dokonale nepružné srážce se zachovává hybnost soustavy. Budeme zkoumat hybnost soutavy před a po srážce a vypočítáme kinetickou energii příslušící pohybu puku ve směru osy \(y\) v okamžiku těsně před srážkou.
Oba puky mají stejnou hmotnost a y-ové souřadnice jejich rychlostí jsou až na znaménko díky symetrii stejné. Ze zákona zachování hybnosti plyne, že hybnost, a tedy i rychlost dvojice puků je po srážce ve směru osy \(y\) nulová.
Rychlost puků ve směru osy \(x\) srážka neovlivní, neboť ráz probíhá ve směru kolmém na tuto osu. Rychlost v tomto směru bude dále růst (se zrychlením \(a = \frac{F}{2m}\)).
Kinetická energie příslušící pohybu puku ve směru osy \(y\) v okamžiku těsně před srážkou se rovná vykonané práci y-ové složky tahové síly na přemístění puku z bodu \([0;l]\) do počátku \([0;0]\). Neboť velikost síly \(T_\mathrm{y}\) není konstantní, závisí na úhlu \(\vartheta\) vztahem (2) a k jejímu výpočtu užijeme integrálního počtu.
\[E_\mathrm{k(y)} = W_{\mathrm{l\to 0}} = \int_l^0 T_\mathrm{y}(\vartheta)\,dy = \int_l^0 -\frac12 F \,\mathrm{tg}\, \vartheta \,dy.\] Protože platí \(y = l\sin \vartheta\) (a diferenciál \(\mathrm{d}y = l\cos\vartheta \,\mathrm{d}\vartheta\)), lze substituovat a integrál dopočítat (nezapomeneme přepočítat meze): \[ \int_l^0 -\frac12 F \,\mathrm{tg}\, \vartheta \,dy = -\frac12 Fl \int_{\frac{\pi}{2}}^0 \sin \vartheta \,d\vartheta = -\frac12 Fl\, \left[-\cos\vartheta\right]_{\pi/2}^0 = \frac12 Fl. \]Mechanická energie, která se při srážce obou puků přemění v energii vnitřní, se rovná dvojnásobku energie \(E_\mathrm{k(y)}\), tj.
\[E' = 2E_\mathrm{k(y)} = Fl.\]Komentář: Úlohu lze řešit i bez užití integrálního počtu
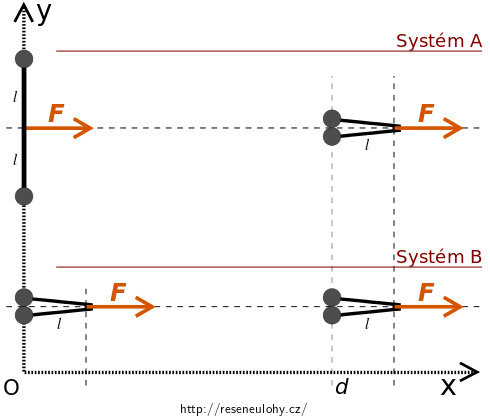
Kromě uspořádání, které jsme dosud řešili (systém A), uvažujme uspořádání B (systém B), kdy se začne působit silou \(\vec F\) na již „sražené“ puky.
V myšlenkovém pokusu necháme oba systémy A i B pohybovat se ve směru osy \(x\) tak, že v čase přiložení síly \(\vec F\) všechny puky leží na ose \(y\).
Odpověď
Při dokonale nepružné srážce puků se ve vnitřní energii přemění kinetické energie puků příslušící složkám rychlostí ve směru rázu o velikosti \(E' = Fl\).