Moment setrvačnosti tyče

Úloha číslo: 516

Určete momenty setrvačností:

A. Tenké homogenní tyče hmotnosti m a délky L s osou otáčení procházející:

a) středem tyče,
b) koncem tyče,
c) bodem v jedné čtvrtině délky tyče.

B. Tenké tyče délky L s osou otáčení v polovině délky, jejíž délková hustota se lineárně mění podle vztahu: λ = λ₀ + ax, kde λ je délková hustota, λ₀ a a jsou konstanty o příslušných jednotkách a x je vzdálenost od osy otáčení.

Opakování teorie a rozbor úlohy
Moment setrvačnosti J tuhého tělesa je tenzor popisující vlastnosti tělesa vyplývající z rozložení hmoty vzhledem k ose otáčení.

Bude-li těleso pravidelné, umístěné ve vhodné soustavě souřadnic a bude-li osa otáčení shodná s jednou z os soustavy, pak se můžeme na J dívat jako na skalár – de facto analogii hmotnosti pro případ rotace.

Nejtypičtější užití (uvažujeme-li pouze skalární vlastnosti):

Kinetická energie rotujícího tělesa: \( E_\mathrm{k} = \frac{1}{2}J\omega^2\,.\)

Moment hybnosti rotujícího tělesa: \( \vec{L} = J\vec{\omega}\,.\)

Moment setrvačnosti hmotného bodu hmotnosti m a ve vzdálenosti r od osy otáčení je:
\[J_\mathrm{hb} = mr^2\,.\]
Zobecnění pro soustavu N hmotných bodů provedeme snadno:
\[J_\mathrm{shb} = \sum^{N}_{i=1} m_\mathrm{i}r_\mathrm{i}^2\,.\]
Budeme-li se dívat na tuhé těleso jako na soustavu nekonečně malých hmotných bodů, pak nás tento pohled přivede k definici momentu servačnosti tuhého tělesa:
\[J_\mathrm{tt} = \int r^2dm\,.\]
Integrovat přes „kousky hmotnosti“ ovšem není příliš praktické. Častěji se tedy setkáme se vzorcem ve tvaru:
\[J_\mathrm{tt} = \int_{V} \rho r^2 dV\,,\]
kde ρ je hustota tělesa a V jeho objem.
Nápověda 1A
Z rozboru úlohy vyplývá, že nejjednodušší bude počítat moment setrvačnosti jako integrál:
\[J = \int_{V} \rho r^2 dV\,.\]
Šel by tento vztah nějakým způsobem zjednodušit, když budeme uvažovat, že tyč je nekonečně tenká – má pouze jeden rozměr – a víme, že je homogenní?
Řešení nápovědy 1A
Tyč budeme brát jako jednorozměrný objekt. Integrál přes objem s využitím objemové hustoty se nám tak zjednoduší na integrál jednorozměrný s délkovou hustotou λ zavedenou vztahem:
\[ \lambda = \frac{m}{L}\,,\]
kde L je celková délka tyče.

Vztah pro výpočet momentu setrvačnosti bude tedy ve tvaru:
\[J = \int\lambda x^2 dx\,.\tag{1}\]
(Můžeme si představit, že tyč rozsekáme na malé elementíky délky dx a posčítáme jejich momenty setrvačnosti.)

Délková hustota λ je konstantní, můžeme ji vytknout před integrál:
\[J = \lambda \int x^2 dx\,.\tag{2}\]
Nápověda 2A
Nakreslete si obrázky pro jednotlivé případy umístění osy otáčení. Uvědomte si, jaké budou meze jednotlivých integrálů (odkud kam budeme přes elementíky sčítat).
Řešení nápovědy 2A
Tyč s osou otáčení v polovině své délky

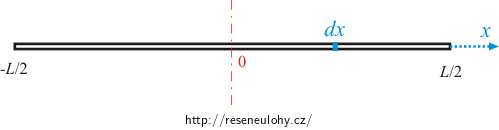
Budeme používat intergrál ve tvaru (2), jeho meze budou od \(-\frac {L}{2}\) do \(\frac {L}{2}\):
\[J = \lambda \int_{-\frac{1}{2}L}^{\frac{1}{2}L} x^2 dx = \lambda \left[\frac{x^{3}}{3}\right]_{-\frac{1}{2}L}^{\frac{1}{2}L} = \frac{\lambda}{3}[\frac{L^3}{8} -(- \frac{L^3}{8})] =\] \[= \lambda \frac{L^3}{12} = \frac{m}{L}\frac {L^3}{12} = \frac{1}{12}mL^2\,.\]
(Je praktičtější si hustotu zpět vhodně převést na hmotnost.)

Tyč upevněná k ose otáčení na svém konci

Postupujeme analogicky:
\[J = \lambda \int_{0}^{L} x^2 dx = \lambda [\frac{1}{3}x^3]^{L}_{0} = \lambda \frac {L^3}{3} =\frac{m}{L}\frac {L^3}{3} = \frac{1}{3}mL^2\,.\]
Osa otáčení prochází tyčí kolmo v jedné čtvrtině její délky

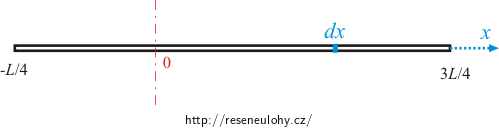
\[J = \lambda \int_{-\frac{1}{4}L}^{\frac{3}{4}L} x^2 dx = \lambda [\frac{1}{3}x^3]_{-\frac{1}{4}L}^{\frac{3}{4}L} =\] \[ = \lambda (\frac{27}{192}L^3+\frac{1}{192}L^3) = \frac{7}{48}\lambda L^3 = \frac{7}{48}\frac{m}{L}L^3 =\frac{7}{48}m L^2\,.\]
Je zjevné, že kdybychom zvolili integrální meze druhým možným způsobem (tj. přisoudili bychom záporné znaménko třem čtvrtinám a kladné jedné polovině délky tyče), integrál by vyšel stejně.
Nápověda 3B
Zamyslete se, jak by šlo upravit integrál z předchozího případu. Co je nutné změnit a co naopak zůstane stejné?
Řešení nápovědy 3B
Stejně jako v předchozím případě zjednodušíme integrál na jednorozměrný (vztah (1)) a dosadíme meze. Hustota však již není konstantní, je potřeba za ni dosadit podle zadání:
\[J = \int_{-\frac{1}{2}L}^{\frac{1}{2}L} \lambda x^2 dx = \int_{-\frac{1}{2}L}^{\frac{1}{2}L} (\lambda_{0} + ax) x^2 dx = \int_{-\frac{1}{2}L}^{\frac{1}{2}L} (\lambda_{0}x^2 + a x^3)dx =\] \[= \lambda_{0} \left[\frac{x^{3}}{3}\right]_{-\frac{1}{2}L}^{\frac{1}{2}L} + a \left[\frac{x^{4}}{4}\right]_{-\frac{1}{2}L}^{\frac{1}{2}L}= \frac{1}{12}\lambda_0 L^3 + \frac{1}{32}aL^4\,.\]
Rychlá kontrola
Všimnětě si, že kdyby byl koeficient a roven nule (hustota by se neměnila), šel by získaný výsledek upravit na již známý moment setrvačnosti homogenní tyče s osou otáčení ve své polovině.
Celkové řešení
A.

Vyjdeme ze vztahu pro moment setrvačnosti:
\[J = \int_{V} \rho r^2 dV\,.\]
Vztah postupně zjednodušíme s ohledem na to, že tyč je nekonečně tenká – má pouze jeden rozměr – a víme, že je homogenní.

Tyč budeme brát jako jednorozměrný objekt. Integrál přes objem s využitím objemové hustoty se nám tak zjednoduší na integrál jednorozměrný s délkovou hustotou λ zavedenou vztahem:
\[ \lambda = \frac{m}{L}\,,\]
kde L je celková délka tyče.

Vztah pro výpočet momentu setrvačnosti bude tedy ve tvaru:
\[J = \int\lambda x^2 dx\,.\tag{1}\]
(Můžeme si představit, že tyč rozsekáme na malé elementíky délky dx a posčítáme jejich momenty setrvačnosti.)

Délková hustota λ je konstantní, můžeme ji vytknout před integrál:
\[J = \lambda \int x^2 dx\,.\tag{2}\]
Tyč s osou otáčení v polovině své délky

Budeme používat intergrál ve tvaru (2), jeho meze budou od \(-\frac {L}{2}\) do \(\frac {L}{2}\):
\[J = \lambda \int_{-\frac{1}{2}L}^{\frac{1}{2}L} x^2 dx = \lambda \left[\frac{x^{3}}{3}\right]_{-\frac{1}{2}L}^{\frac{1}{2}L} = \frac{\lambda}{3}[\frac{L^3}{8} -(- \frac{L^3}{8})] =\] \[= \lambda \frac{L^3}{12} = \frac{m}{L}\frac {L^3}{12} = \frac{1}{12}mL^2\,.\]
(Je praktičtější si hustotu zpět vhodně převést na hmotnost.)

Tyč upevněná k ose otáčení na svém konci

Postupujeme analogicky:
\[J = \lambda \int_{0}^{L} x^2 dx = \lambda [\frac{1}{3}x^3]^{L}_{0} = \lambda \frac {L^3}{3} =\frac{m}{L}\frac {L^3}{3} = \frac{1}{3}mL^2\,.\]
Osa otáčení prochází tyčí kolmo v jedné čtvrtině její délky

\[J = \lambda \int_{-\frac{1}{4}L}^{\frac{3}{4}L} x^2 dx = \lambda [\frac{1}{3}x^3]_{-\frac{1}{4}L}^{\frac{3}{4}L} =\] \[ = \lambda (\frac{27}{192}L^3+\frac{1}{192}L^3) = \frac{7}{48}\lambda L^3 = \frac{7}{48}\frac{m}{L}L^3 =\frac{7}{48}m L^2\,.\]
Je zjevné, že kdybychom zvolili integrální meze druhým možným způsobem (tj. přisoudili bychom záporné znaménko třem čtvrtinám a kladné jedné polovině délky tyče), integrál by vyšel stejně.

B.

Stejně jako v předchozím případě zjednodušíme integrál na jednorozměrný (vztah (1)) a dosadíme meze. Hustota však již není konstantní, je potřeba za ni dosadit podle zadání:
\[J = \int_{-\frac{1}{2}L}^{\frac{1}{2}L} \lambda x^2 dx = \int_{-\frac{1}{2}L}^{\frac{1}{2}L} (\lambda_{0} + ax) x^2 dx = \int_{-\frac{1}{2}L}^{\frac{1}{2}L} (\lambda_{0}x^2 + a x^3)dx =\] \[= \lambda_{0} \left[\frac{x^{3}}{3}\right]_{-\frac{1}{2}L}^{\frac{1}{2}L} + a \left[\frac{x^{4}}{4}\right]_{-\frac{1}{2}L}^{\frac{1}{2}L}= \frac{1}{12}\lambda_0 L^3 + \frac{1}{32}aL^4\,.\]
Odpověď
Moment setrvačnosti tenké homogenní tyče hmotnosti m a délky L s osou otáčení procházející kolmo...
- ...v polovině tyče je: \(J = \frac{1}{12}mL^2,\)
- ...jedním koncem tyče je: \(J = \frac{1}{3}mL^2,\)
- ...v jedné čtvrtině tyče je: \(J = \frac{7}{48}mL^2.\)
Moment setrvačnosti tyče délky L, jejíž hustota se lineárně mění (viz zadání), je: \[J = \frac{1}{12}\lambda_0 L^3 + \frac{1}{32}aL^4\,.\]
Rychlá kontrola
Srovnejte tvar všech výsledků a udělejte jednotkovou zkoušku. Je jasné, že dokud do hry nevstoupí proměnlivá hustota tělesa nebo jiná osa než kolmá, jde prakticky jen o určení multiplikativní konstanty před výrazem mL².