Červ na tělesové úhlopříčce

Úloha číslo: 187

Červ se prokousává konstantní rychlostí v po tělesové úhlopříčce kvádru o hranách a, b, c. V čase t = 0 byl červ v horním vrcholu C' a směřoval k vrcholu A, který zvolte za počátek soustavy souřadnic. Popište průběh polohy červa (tj. závislost souřadnic červa na čase).

Nápověda 1
Nakreslete si obrázek, který situaci popisuje. Víte, že pohyb červa je rovnoměrný přímočarý. Pokuste se vyjádřit průběh x-ové, y-ové a z-ové souřadnice na čase.
Obrázek k nápovědě 1:
Řešení k nápovědě 1
Červ se pohybuje rovnoměrně přímočaře. To znamená, že jeho souřadnice x, y, z závisí na čase t podle vztahů:

\[x\,=\,x_{0}+v_\mathrm{x}t\,,\]

\[y\,=\,y_{0}+v_\mathrm{y}t\,,\]

\[z\,=\,z_{0}+v_\mathrm{z}t\,,\]

kde x₀, y₀, z₀ jsou souřadnice červa v čase t= 0 s a v_x, v_y, v_z složky rychlosti ve směru os x, y, z.
Nápověda 2
Pro rovnoměrný přímočarý pohyb je závislost souřadnic na čase dána vztahy: x = x₀ + v_xt, y = y₀ + v_yt, z = z₀ + v_zt. Které veličiny potřebujeme v těchto vztazích určit?
Řešení k nápovědě 2
Potřebujeme určit:

a) konstanty x₀, y₀ a z₀,

b) složky rychlosti v_x, v_y a v_z.
Nápověda 3
Určení konstant x₀, y₀ a z₀:

Konstanty x₀, y₀ a z₀ vyjadřují souřadnice x, y, z na počátku pohybu, kdy je červ v bodě C'. Jaké zde má souřadnice?
Řešení k nápovědě 3
Na počátku pohybu (v čase t = 0) byl červ v bodě C'. Jeho souřadnice jsou tedy identické se souřadnicemi bodu C':

\[x(0)\,\equiv\,x_{0}\,=\,a\,,\]

\[y(0)\,\equiv\,y_{0}\,=\,b\,,\]

\[z(0)\,\equiv\,z_{0}\,=\,c\,.\]
Nápověda 4
Určení složek rychlosti v_x, v_y a v_z:

Vektor rychlosti míří ve směru úhlopříčky kvádru, znáte jeho velikost – to je v. Není možné určit složky rychlosti pomocí této velikosti a geometrických úvah (tedy z obrázku)?

Znáte délky stran a, b, c. Jaký je poměr délek těchto stran vůči délce tělesové úhlopříčky l? A jaký je poměr složek rychlostí v_x, v_y, v_z vůči velikosti celkové rychlosti v?

Nelze do výpočtu zapojit například goniometrické funkce?
Řešení k nápovědě 4
Problém můžeme řešit dvěma způsoby:

1. způsob: Použijeme geometrickou představu a znalost goniometrických funkcí. Složka rychlosti ve směru osy z bude mít velikost:

\[v_\mathrm{z}\,=\,-v\,\sin{\alpha}\,=\,-v\,\frac{c}{l}\,,\]

kde α je úhel mezi tělesovou úhlopříčkou a podstavou kvádru a l délka tělesové úhlopříčky, \[l\,=\,\sqrt{a^{2}+b^{2}+c^{2}}\,.\]

Analogicky dostaneme pro zbylé dvě složky rychlosti:

\[v_\mathrm{x}\,=\,-v\,\frac{a}{l}\,,\]

\[v_\mathrm{y}\,=\,-v\,\frac{b}{l}\,.\]

2. způsob: Vyjdeme z toho, že k uražení dráhy l potřebuje červ čas t:

\[t\,=\,\frac{l}{v}\,.\]

V tomto čase dorazí do bodu A = [0,0,0] a musí tedy platit (např. pro souřadnici x):

\[0\,=\,a+v_\mathrm{x}\,\frac{l}{v} \hspace{10px}\Rightarrow \hspace{10px}v_\mathrm{x}\,=\,-v\,\frac{a}{l}.\]

Analogicky platí pro ostatní souřadnice.

Závislost souřadnic červa na čase je tedy dána vztahy:
\[x\,=\,a+v_\mathrm{x}t\,=\,a-v\,\frac{a}{l}t\,,\] \[y\,=\,b+v_\mathrm{y}t\,=\,b-v\,\frac{b}{l}t\,,\] \[z\,=\,c+v_\mathrm{z}t\,=\,c-v\,\frac{c}{l}t\,.\]
Komentář - alternativní řešení
Možný alternativní přístup:

Jinou možností odvození je vyjít z:

a) podmínek pro polohu červa v čase t = 0,

b) podmínek pro polohu červa na konci pohybu.

V čase t = 0 je dán jeho polohový vektor: r = (x, y, z) = (a, b, c), na konci je jeho poloha (0, 0, 0).

Z obecných vztahů pro rovnoměrný pohyb: x = x₀ + v_xt (pro y a z podobně) lze pak určit hodnoty konstant x₀, y₀, z₀, v_x, v_y, v_z.
Celkové řešení
Nakreslíme obrázek situace:

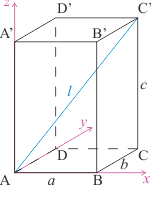
Máme zadány délky a, b, c hran kvádru, délka jeho tělesové úhlopříčky je:

\[l\,=\,\sqrt{a^{2}+b^{2}+c^{2}}\,.\]

Na počátku (v čase t = 0) byl červ v bodě C', pro jeho souřadnice tedy platilo:
\[x(0)\,\equiv\,x_{0}\,=\,a\,,\] \[y(0)\,\equiv\,y_{0}\,=\,b\,,\] \[z(0)\,\equiv\,z_{0}\,=\,c\,.\]
Červ se pohybuje rovnoměrně přímočaře. To znamená, že jeho souřadnice x, y, z závisí na čase t podle vztahů:
\[x\,=\,x_{0}+v_\mathrm{x}t\,,\] \[y\,=\,y_{0}+v_\mathrm{y}t\,,\] \[z\,=\,z_{0}+v_\mathrm{z}t\,.\]
Hodnoty x₀, y₀, z₀ už známe, zbývá tedy určit složky rychlosti: v_x, v_y, v_z do směrů os x, y, z.

Odvození složek rychlosti vycházející z geometrické představy:

Složka rychlosti ve směru osy z bude mít velikost:
\[v_\mathrm{z}\,=\,-v\,\sin{\alpha}\,=\,-v\,\frac{c}{l}\,.\]
(Úhel α je úhel mezi tělesovou úhlopříčkou a podstavou kvádru.)

Analogicky dostaneme:
\[v_\mathrm{x}\,=\,-v\,\frac{a}{l}\,,\] \[v_\mathrm{y}\,=\,-v\,\frac{b}{l}\,.\]
Odvození složek rychlosti ze vztahů pro souřadnice:

Do bodu A = [0,0,0] červ dorazí za čas: \(t\,=\,\frac{l}{v}\,.\) Zároveň pro tento bod platí (např. x-ová souřadnice):
\[0\,=\,a+v_\mathrm{x}\,\frac{l}{v} \hspace{10px}\Rightarrow \hspace{10px}v_\mathrm{x}\,=\,-v\,\frac{a}{l}.\]
Pro ostatní souřadnice je odvození stejné.

Výsledné souřadnice červa:

Souřadnice x červa: \[x\,=\,a+v_\mathrm{x}t\,=\,a-v\,\frac{a}{l}t\,.\]

Souřadnice y červa: \[y\,=\,b+v_\mathrm{y}t\,=\,b-v\,\frac{b}{l}t\,.\]

Souřadnice z červa: \[z\,=\,c+v_\mathrm{z}t\,=\,c-v\,\frac{c}{l}t\,.\]
Alternativní celkové řešení
Rovnoměrný pohyb červa je popsán vztahy:

x = x₀ + v_xt,

y = y₀ + v_yt,

z = z₀ + v_zt,

kde x₀, y₀, z₀, v_x, v_y, v_z jsou konstanty.
- Určení souřadnicových konstant:
  V čase t = 0 s (tedy je-li červ v bodě C') musí platit:
  
  x(0) = a,
  
  y(0) = b,
  
  z(0) = c.
  
  Odtud po dosazení vyjde: x₀ = a, y₀ = b, z₀ = c.
- Určení složek rychlosti:
  V čase t_K (který neznáme) musí být červ v bodě A = [0,0,0], tj.:
  
  x(t_K) = a + v_xt_K = 0,
  
  y(t_K) = b + v_yt_K = 0,
  
  z(t_K) = c + v_zt_K = 0.
  
  Odtud: \(v_\mathrm{x}\,=\,\frac{-a}{t_\mathrm{K}}\), \(v_\mathrm{y}\,=\,\frac{-b}{t_\mathrm{K}}\), \(v_\mathrm{z}\,=\,\frac{-c}{t_\mathrm{K}}\).
  
  Velikost rychlosti: \[v\,=\,\sqrt{v_\mathrm{x}^{2}+v_\mathrm{y}^{2}+v_\mathrm{z}^{2}}\,.\]
  
  Po dosazení: \[v\,=\,\frac{\sqrt{a^{2}+b^{2}+c^{2}}}{t_\mathrm{K}}\,=\,\frac{l}{t_\mathrm{K}}\,.\]
  
  Odtud vypočteme t_K a dosazením dostáváme pro složky rychlosti: \(v_\mathrm{x}\,=\,-v\,\frac{a}{l}\,,\) \(v_\mathrm{y}\,=\,-v\,\frac{b}{l}\,\) a \(v_\mathrm{z}\,=\,-v\,\frac{c}{l}\,.\)
  
  Dále pokračujeme dosazením do rovnic popisujících rovnoměrný pohyb červa (na začátku tohoto způsobu řešení).
Výsledek
Pohyb červa je popsán vztahy:
\[x\,=\,a+v_\mathrm{x}t\,=\,a-v\,\frac{a}{l}t\,,\] \[y\,=\,b+v_\mathrm{y}t\,=\,b-v\,\frac{b}{l}t\,,\] \[z\,=\,c+v_\mathrm{z}t\,=\,c-v\,\frac{c}{l}t\,,\]
kde \(l\,=\,\sqrt{a^{2}+b^{2}+c^{2}}\) je délka tělesové úhlopříčky kvádru. (Osy míří podél hran o délkách a, b, c.)