Voda stříkající z nádoby
Úloha číslo: 925
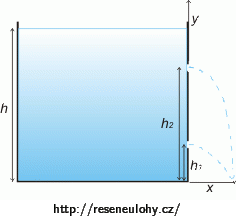
Nádoba má ve stěně vyvrtány dva otvory, jeden ve výšce h1 ode dna a druhý ve výšce h2. V jaké výšce h musí být hladina vody v nádobě, chceme-li, aby voda z obou otvorů stříkala do stejné vzdálenosti x? Odpor vzduchu zanedbejte.
Řešte nejprve obecně a potom pro hodnoty h1 = 10 cm a h2 = 30 cm.
Zápis
h1 = 10 cm výška prvního otvoru ode dna h2 = 30 cm výška druhého otvoru ode dna x délka dostřiku h = ? výška hladiny v nádobě Rozbor
Při řešení úlohy využijeme jednak poznatky z hydromechaniky a také poznatky o vodorovném vrhu. Vyjádříme si, jak daleko voda v obou případech dostříkne. K tomu budeme potřebovat znát rychlosti výtoku vody z obou otvorů. Ty zjistíme z Bernoulliho rovnice.
Nápověda 1
Jak vypočítáme délku dostřiku \(x\)?
Nápověda 2
Co dále platí pro \(x_{1}\) a \( x_{2}\)?
Nápověda 3
Jak vypočítáme časy \(t_{1}\), \(t_{2}\), za které voda dopadne na podložku?
Nápověda 4
Jak vypočítáme rychlosti \(v_{1}\) a \(v_{2}\), kterými voda vystřikuje z otvorů?
Nápověda 5
Použijte vztah (3), dosaďte do něj zjištěné časy a rychlosti a vyjádřete hledanou výšku hladiny.
Celkové řešení
Výpočet délky dostřiku
Délku dostřiku \(x\) vypočítáme dle vztahu:
\[x=vt,\]kde \(v\) je rychlost vody v okamžiku výtoku a \(t\) je čas, za který voda dopadne do vzdálenosti \(x\).
První výška
Pro vodu, která vystřikuje z výšky \(h_{1}\), bude platit:
\[x_{1}=v_{1}t_{1}.\tag{1}\]Druhá výška
Pro vodu, která vystřikuje z výšky \(h_{2}\), bude platit:
\[x_{2}=v_{2}t_{2}.\tag{2}\]Chceme, aby voda z obou otvorů dopadala do stejné vzdálenosti, proto bude platit:
\[x_{1}=x_{2}.\]Dosadíme za \(x_{1}\), \(x_{2}\) dle vztahů (1), (2) a dostáváme:
\[v_{1}t_{1}=v_{2}t_{2}.\tag{3}\]Výpočet času
Dobu \(t\), za kterou voda dopadne do vzdálenosti \(x\), vypočítáme ze vztahu:
\[y=\frac{1}{2}gt^2,\]kde \(g\) je tíhové zrychlení a \(y\) je výška, ze které voda padá.
První výška
Pro vodu, která vystřikuje z výšky \(h_{1}\), bude platit:
\[h_{1}=\frac{1}{2}gt^2_{1}.\]Obě strany rovnice upravíme tak, že je vydělíme \(\frac{1}{2}g\):
\[\frac{2h_{1}}{g}=t^2_{1}.\]Obě strany rovnice odmocníme a dostaneme \(t_{1}\):
\[t_{1}=\sqrt{\frac{2h_{1}}{g}}.\tag{4}\]Druhá výška
Pro vodu, která vystřikuje z výšky \(h_{2}\), bude platit:
\[h_{2}=\frac{1}{2}gt^2_{2}.\]Obě strany rovnice upravíme tak, že je vydělíme \(\frac{1}{2}g\):
\[\frac{2h_{2}}{g}=t^2_{2}.\]
Obě strany rovnice odmocníme a dostaneme \(t_{2}\):
\[t_{2}=\sqrt{\frac{2h_{2}}{g}}.\tag{5}\]Výpočet rychlosti
Rychlost vody \(v\) získáme z Bernoulliho rovnice:
\[\frac{1}{2}\rho v^2_\mathrm{i}+\rho g h_\mathrm{i}+p_\mathrm{i}=\frac{1}{2}\rho v^2_\mathrm{e}+\rho gh_\mathrm{e}+p_\mathrm{e},\]kde \(\rho\) je hustota vody, \(p\) je tlak a \(h\) je výška nad podložkou. Index \(i\) znamená uvnitř nádoby a index \(e\) vně.
Rychlost vody v místě výtoku uvnitř nádoby je u obou otvorů nulová. Tedy:
\[\frac{1}{2}\rho v^2_\mathrm{i}=0.\]Výška nad podložkou je uvnitř i vně stejná, člen \(\rho gh\) odpovídající polohové energii vypadne. Tlak v místě výtoku uvnitř nádoby bude dán součtem atmosférického tlaku \(p_\mathrm{a}\) a hydrostatického tlaku \(p_\mathrm{h}=(h-h_\mathrm{i})\rho g\) sloupce vody nad výtokovým otvorem. Tedy:
\[p_\mathrm{i}=p_\mathrm{a}+(h-h_\mathrm{i})\rho g .\]Tlak v místě výtoku vně nádoby je pro oba otvory roven atmosférickému tlaku. Přepíšeme Bernoulliho rovnici pro oba případy.
První výška
Pro vodu, která vystřikuje z výšky \(h_{1}\), bude platit:
\[ p_\mathrm{a}+\rho g( h- h_{1})=\frac{1}{2} \rho v^2_{1}+p_\mathrm{a}.\]Odečteme od obou stran \(p_{a}\) a vydělíme \(\rho\):
\[ g( h- h_{1})=\frac{1}{2} v^2_{1}.\]Obě strany rovnice upravíme tak, že je vynásobíme \(2\) a odmocníme je:
\[ v_{1}=\sqrt{2g( h- h_{1})}.\tag{6}\]Druhá výška
Pro vodu, která vystřikuje z výšky \(h_{2}\), bude platit:
\[ p_\mathrm{a}+\rho g( h- h_{2})=\frac{1}{2} \rho v^2_{2}+p_\mathrm{a}.\]Odečteme od obou stran \(p_{a}\) a vydělíme \(\rho\):
\[ g( h- h_{2})=\frac{1}{2} v^2_{2}.\]Obě strany rovnice upravíme tak, že je vynásobíme \(2\) a odmocníme je:
\[ v_{2}=\sqrt{2g( h- h_{2})}.\tag{7}\]Dosazení do vztahu (3)
Do vztahu (3) dosadíme za \(t_{1},t_{2},v_{1},v_{2}\) vztahy (4),(5), (6) a (7).
\[v_{1}t_{1}=v_{2}t_{2},\] \[\sqrt{2g( h- h_{1})}\sqrt{\frac{2h_{1}}{g}}=\sqrt{2g( h- h_{2})}\sqrt{\frac{2h_{2}}{g}}.\]Obě strany rovnice upravíme tak, že je umocníme na druhou:
\[2g( h- h_{1})\frac{2h_{1}}{g}= 2g( h- h_{2})\frac{2h_{2}}{g}.\]\(g\) se vykrátí a obě strany rovnice vydělíme \(4\):
\[( h- h_{1})h_{1}=( h- h_{2})h_{2}.\]Roznásobíme závorky, členy obsahující \(h\) přesuneme na levou stranu a zbylé na pravou stranu rovnice:
\[hh_{1}-hh_{2}=h^2_{1}-h^2_{2}.\]Vytkneme \(h\) a člen \(h^2_{1}-h^2_{2}\) rozepíšeme jako součin:
\[h(h_{1}-h_{2})=(h_{1}-h_{2})(h_{1}+h_{2}).\]Vykrátíme \((h_{1}-h_{2})\) a dostaneme:
\[h=h_{1}+h_{2}.\tag{8}\]Číselné řešení
Zadané hodnoty \(h_{1}=10\,\mathrm{cm}\) a \(h_{2}=30\,\mathrm{cm}\) dosadíme do vztahu (8):
\[h=h_{1}+h_{2}=10\,\mathrm{cm}+30\,\mathrm{cm}=40\,\mathrm{cm}.\]Odpověď
Voda z obou otvorů bude stříkat do stejné vzdálenosti, pokud bude pro výšku \(h\) hladiny vody v nádobě platit:
\(h=h_{1}+h_{2}.\)Pro zadané hodnoty \(h_{1}=10\,\mathrm{cm}\) a \(h_{2}=30\,\mathrm{cm}\) bude \(h=40\,\mathrm{cm}.\)





