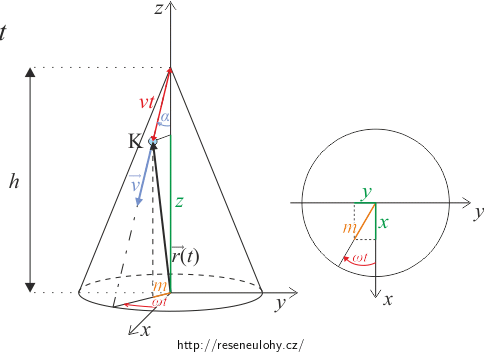Pohyb kapky
Úloha číslo: 122
Kužel výšky h se otáčí kolem své osy ve směru otáčení hodinových ručiček stálou úhlovou rychlostí ω. Povrchová přímka svírá s osou kužele úhel α. Od vrcholu kužele začne v čase t = 0 s stékat po povrchové přímce kapka stálou rychlostí v vzhledem ke kuželu. V pevném souřadném systému x, y, z zvoleném tak, že osa z je osou kužele a osy x, y leží v jeho podstavě, popište průběh polohového vektoru kapky a průběh velikosti její rychlosti.
Nápověda 1: Obrázek situace
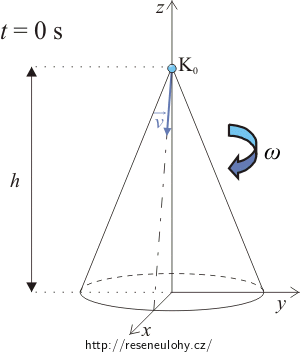
Počátek souřadné soustavy zvolte ve středu podstavy kužele a počáteční polohu kapky na vrcholu kužele.
Nakreslete situaci pro čas t = 0 s a vyznačte polohu kapky.
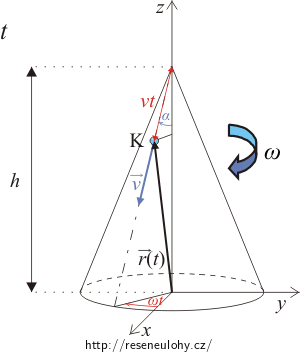
Pak nakreslete situaci pro čas t, vyznačte polohu kapky, kam až se za čas t na kuželi dostala, i její polohový vektor.
Do obrázku vyznačte i průmět polohového vektoru do osy z a do roviny x, y.
Nápověda 2: Průběh polohového vektoru kapky
Z obrázku z předchozí nápovědy sestavte rovnice pro průmět polohového vektoru kapky do osy z a průmět m polohového vektoru kapky do roviny xy.
Dále zapište rovnice průmětu m do os x a y.
Z těchto rovnic pak napište průběh polohového vektoru kapky.
Nápověda 3: Průběh velikost rychlosti kapky
Vyjádřete si nejprve složky rychlosti vx, vy, vz. Jakým způsobem je z parametrických rovnic ve směru souřadnicových os získáte?
Pak zapište průběh velikosti rychlosti kapky.
CELKOVÉ ŘEŠENÍ
Obrázek 1:
Průmět polohového vektoru do osy z:
\[z\,=\,h-vt\cos\alpha.\]Průmět polohového vektoru do roviny xy:
\[m\,=\,vt\sin\alpha.\]Průmět m do os x a y:
\[x\,=\,m\cos\omega{t}\,=\,vt\sin\alpha\cos\omega{t},\] \[y\,=\,-m\sin\omega{t}\,=\,-vt\sin\alpha\sin\omega{t}.\]Průběh polohového vektoru kapky:
\[\vec{r}\left(t\right)\,=\,vt\sin\alpha\cos\omega{t}\vec{\,i\,}-vt\sin\alpha\omega{t}\vec{\,j\,}+(h-vt\cos\alpha)\vec{\,k\,},\]kde \(\vec{\,i\,}\), \(\vec{\,j\,}\), \(\vec{\,k\,}\) jsou jednotkové vektory.
Složky rychlosti získáme derivací souřadnic podle času:
\[v_\mathrm{x}\,=\,\frac{\mathrm{d}x}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(vt\sin\alpha\cos\omega{t}\right)\,=\, v\sin\alpha\cos\omega{t}-v\omega{t}\sin\alpha\sin\omega{t},\] \[v_\mathrm{y}\,=\,\frac{\mathrm{d}y}{\mathrm{d}t}\,=\,\frac{\mathrm{d}}{\mathrm{d}t}\left(-vt\sin\alpha\sin\omega{t}\right)\,=\, -v\sin\alpha\sin\omega{t}-v\omega{t}\sin\alpha\cos\omega{t},\] \[v_\mathrm{z}\,=\,\frac{\mathrm{d}z}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(h-vt\cos\alpha\right) \,=\, -v\cos\alpha.\]Průběh velikosti rychlosti kapky:
\[\left|\vec{v}_\mathrm{v}\left(t\right)\right|\,=\,\sqrt{v_\mathrm{x}^{2}+v_\mathrm{y}^{2}+v_\mathrm{z}^{2}},\]
\[v_\mathrm{x}^{2}\,=\,\left(v\sin\alpha\cos\omega{t}-v\omega{t}\sin\alpha\sin\omega{t}\right)^{2}\,=\] \[\,=\,v^{2}\sin^{2}\alpha\cos^{2}\omega{t}-2v^{2}\omega{t}\sin^{2}\alpha\sin\omega{t}\cos\omega{t}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\sin^{2}\omega{t},\]
\[v_\mathrm{y}^{2}\,=\,\left(-v\sin\alpha\sin\omega{t}-v\omega{t}\sin\alpha\cos\omega{t}\right)^{2}\,=\] \[\,=\,v^{2}\sin^{2}\alpha\sin^{2}\omega{t}+2v^{2}\omega{t}\sin^{2}\alpha\sin\omega{t}\cos\omega{t}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\cos^{2}\omega{t},\]
\[v_\mathrm{z}^{2}\,=\, \left(-v\cos\alpha\right)^{2}\,=\, v^{2}\cos^{2}\alpha,\]
\[v_\mathrm{x}^{2}+ v_\mathrm{y}^{2}+ v_\mathrm{z}^{2}\,=\, v^{2}\sin^{2}\alpha\cos^{2}\omega{t}+v^{2}\sin^{2}\alpha\sin^{2}\omega{t}+\] \[\,+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\sin^{2}\omega{t}+ v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\cos^{2}\omega{t}+v^{2}\cos^{2}\alpha\,=\] \[\,=\,v^{2}\sin^{2}\alpha+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha+v^{2}\cos^{2}\alpha\,=\] \[=\,v^{2}\sin^{2}\alpha+v^{2}\cos^{2}\alpha+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha\,=\] \[\,=\,v^{2}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha,\]
\[\left|\vec{v}_\mathrm{v}\left(t\right)\right|\,=\,\sqrt{v_\mathrm{x}^{2}+v_\mathrm{y}^{2}+v_\mathrm{z}^{2}}\,=\,\sqrt{v^{2}+v^{2}\omega^{2}{t}^{2}\sin^{2}\alpha},\]
\[\left|\vec{v}_\mathrm{v}\left(t\right)\right|\,=\,\sqrt{v^{2}+(vt\omega\sin\alpha)^{2}}.\]Odpověď
Průběh polohového vektoru kapky je:
\[\vec{r}\left(t\right)\,=\,vt\sin\alpha\cos\omega{t}\vec{\,i\,}-vt\sin\alpha\sin\omega{t}\vec{\,j\,}+(h-vt\cos\alpha)\vec{\,k\,},\]kde \(\vec{\,i\,}\), \(\vec{\,j\,}\), \(\vec{\,k\,}\) jsou jednotkové vektory.
Průběh velikosti rychlosti kapky:
\[\left|\vec{v}_\mathrm{v}\left(t\right)\right|\,=\,\sqrt{v_\mathrm{x}^{2}+v_\mathrm{y}^{2}+v_\mathrm{z}^{2}}\,=\,\sqrt{v^{2}+\left(vt\omega\sin\alpha\right)^{2}}.\]Vizualizace pohybu
Následující aplet slouží k vizualizaci pohybu kapky na rotujícím kuželu. Polohu kapky udává polohový vektor \(\vec{r}_{(t)}\), který je znázorněn modře. Vektor rychlosti \(\vec{v}_{(t)}\) je znázorněn červeně. Kliknutím na tlačítko „Zapnout animaci“ se spustí animace pohybu, opětovným kliknutím se animace zastaví. Kliknutím na tlačítko „Zobrazit stopu kapky“ se zapne, nebo naopak vypne stopa bodu K. Obdobně tlačítko „Zobrazit trajektorii kapky“ vykreslí trajektorii bodu K. Tlačítko „Reset“ vrátí aplet do původního stavu.
Z apletu je dobře vidět, že trajektorií kapky stékající po rotujícím kuželu je jakási „rozevírající se šroubovice“.