Basketbalista
Úloha číslo: 132
Obroučka koše na basketbal se nachází ve výšce h1 nad podlahou. Střed koše je ve vodorovné vzdálenosti L od čáry trestného hodu. Basketbalista hází trestné hody, přičemž míč opouští jeho ruku v poloze, kdy jeho střed je přesně nad čárou trestného hodu ve výšce h2 nad podlahou.
Optimální elevační úhel α je takový, při němž střed míče projde středem obroučky a přitom je zapotřebí co nejmenší počáteční rychlost míče. Dokažte obecně, že tento úhel má velikost α = 45˚ + β/2, kde β je záměrný úhel, tj. odchylka spojnice středu obroučky a počátečního bodu vrhu od vodorovné roviny.
Určete optimální elevační úhel pro zadané hodnoty a vypočtěte příslušnou velikost počáteční rychlosti míče.
Odpor vzduchu zanedbejte.
Řešte pro hodnoty: h1 = 3,05 m, L = 5,425 m, h2 = 2,45 m, g = 9,81 m·s-2 .
Zápis
h1 = 3,05 m výška obroučky koše nad podlahou h2 = 2,45 m výška středu míče nad podlahou v okamžiku odhození L = 5,425 m vodorovná vzdálenost středu koše od čáry trestného hodu α = ? optimální elevační úhel v0 = ? (m·s−1)
velikost počáteční rychlosti míče odpovídající optimálnímu elevačnímu úhlu Z tabulek: g = 9,81 m·s−2
tíhové zrychlení
Nápověda 1: Obrázek situace
Nakreslete obrázek zachycující danou situaci, vyznačte do něj elevační a záměrný úhel, vzdálenost L a výšku obroučky koše nad místem, ze kterého házíme míč.
Nápověda 2: Pohyb míče ve vodorovném a svislém směru
Jaký pohyb vykonává míč ve vodorovném směru? Jaký pohyb vykonává míč ve svislém směru?
Nápověda 3: Rychlost míče ve vodorovném a svislém směru
Jaká je rychlost míče ve vodorovném směru a jak se mění s časem x-ová souřadnice míče?
Jaká je rychlost míče ve svislém směru a jak se mění s časem y-ová souřadnice míče?
Jaké hodnoty budou mít souřadnice x a y v okamžiku, kdy míč doletí do obroučky koše? Napište příslušné vztahy a vyjádřete z nich druhou mocninu počáteční rychlosti v02 (využijte ještě vztah tg β = H/L).
Nápověda 4: Minimální hodnota výrazu
Pro jaký úhel α bude hodnota výrazu pro v02 minimální?
Nápověda 5: Počáteční rychlost pro optimální úhel
Spočítejte počáteční rychlost v0 pro optimální úhel α, tedy pro případ, kdy sin(2α−β) = 1. Sinus a kosinus úhlu β vyjádřete pomocí vzdáleností H a L.
CELKOVÉ ŘEŠENÍ:
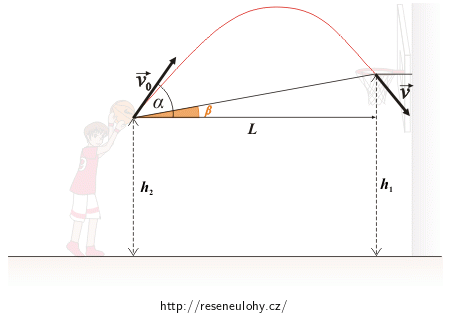
Označíme si L a H vodorovnou a svislou vzdálenost středu obroučky od počátečního bodu vrhu, α elevační úhel, β záměrný úhel, t dobu letu, v0 počáteční rychlost míče, v rychlost míče při průletu košem (viz obrázek 1, 2).
Obrázek 1:
\[H = h_1 - h_2\]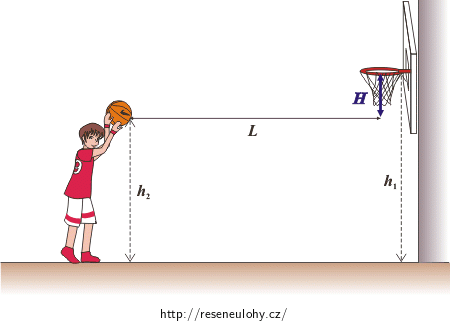
Obrázek 2:
Ve vodorovném směru vykonává míč rovnoměrný přímočarý pohyb.Ve svislém směru vykonává míč vrh svislý vzhůru.
Platí:
\[v_\mathrm{x}=v_0\cos\alpha\,,\] \[v_\mathrm{y}=v_0\sin\alpha-gt\,,\] \[x=v_0t\cos\alpha\,,\] \[y=v_0t\sin\alpha-\frac{1}{2}gt^{2}\,.\]V okamžiku, kdy míč doletí do obroučky koše, bude platit:
\[x=L=v_0t\cos\alpha\,.\]Tedy:
\[t=\frac{L}{v_0\cos\alpha}\,,\] \[y=H=v_0t\sin\alpha-\frac{1}{2}gt^{2}=Ltg\alpha-\frac{gL^{2}}{2v_0^{2}\cos^{2}\alpha}\,.\]Odtud:
\[\frac{gL^{2}}{2v_0^{2}\cos^{2}\alpha} = Ltg\alpha- H\,,\] \[\frac{gL^{2}}{Ltg\alpha- H} = 2v_0^{2}\cos^{2}\alpha\,,\] \[v_0^{2}=\frac{gL^{2}}{2(Ltg\alpha-H)\cos^{2}\alpha}=\frac{gL^{2}}{2(L\sin\alpha\cos\alpha-Hcos^{2}\alpha)}\,.\]Po dosazení \(H=Ltg\beta\) a úpravě dostaneme:
\[v_0^{2}=\frac{gL^{2}}{2(L\sin\alpha\cos\alpha-Ltg\beta\cos^{2}\alpha)}=\frac{gL}{sin2\alpha-tg\beta(1+\cos2\alpha)}\,,\] \[v_0^{2}=\frac{gL\cos\beta}{\sin2\alpha\cos\beta-\sin\beta-\sin\beta\cos2\alpha}=\frac{gL\cos\beta}{\sin(2\alpha-\beta)-\sin\beta}\,.\]Poznámka: Při úpravách jsme použili následující goniometrické vztahy:
\[2\sin\alpha\cos\alpha = \sin2\alpha\,,\] \[\cos2\alpha = cos^{2}\alpha - sin^{2}\alpha\,,\] \[\sin(2\alpha-\beta) = sin2\alpha\cos\beta - cos2\alpha\sin\beta\,.\]Hodnota výrazu bude minimální, jestliže bude maximální hodnota jmenovatele, tedy jestliže:
\[\sin(2\alpha-\beta)=1\,,\] \[2\alpha-\beta=90^{\circ}\,.\]Tedy, když platí:
\[\alpha=45^{\circ}+\frac{\beta}{2}\,.\]V takovém případě:
\[v_0^{2}=\frac{gL\cos\beta}{1-\sin\beta}\,.\]Platí:
\[\cos\beta = \frac{L}{\sqrt{H^{2}+L^{2}}}\,, \] \[\sin\beta = \frac{H}{\sqrt{H^{2}+L^{2}}}\,. \]S použitím \(H = h_1 - h_2\):
\[\cos\beta = \frac{L}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}\,, \] \[\sin\beta = \frac{h_1 - h_2}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}\,.\]Pak:
\[v_0^{2}=\frac{\frac{gL^{2}}{\sqrt{H^{2}+L^{2}}}}{1-\frac{H}{\sqrt{H^{2}+L^{2}}}}=\frac{gL^{2}}{\sqrt{H^{2}+L^{2}}-H}=g\left(\sqrt{H^{2}+L^{2}}+H\right)\,.\]S použitím \(H = h_1 - h_2\):
\[v_0^{2}=g\left(\sqrt{(h_1 - h_2)^{2}+L^{2}}+(h_1 - h_2)\right)\,.\]Číselně pro zadané hodnoty:
\[\sin\beta = \frac{3{,}05-2{,}45}{\sqrt{(3{,}05 - 2{,}45)^{2}+5{,}425^{2}}}.\] Z toho plyne: \(\beta \dot{ = } 6^{\circ}\). Pak: \[\alpha=45^{\circ}+\frac{\beta}{2}\,,\] \[\alpha\dot{=}48^{\circ}\,.\] Dále: \[v_0^{2}=9{,}81\left(\sqrt{(3{,}05 - 2{,}45)^{2}+5{,}425^{2}}+(3{,}05 - 2{,}45)\right)\,\mathrm{m^{2} \cdot s^{-2}}\,,\] \[v_0\dot{=}7{,}7\,\mathrm{m \cdot s^{-1}}\,.\]Odpověď:
Optimální elevační úhel je:
\(\alpha=45^{\circ}+\frac{\beta}{2},\) kde \(\sin\beta = \frac{h_1 - h_2}{\sqrt{(h_1 - h_2)^{2}+L^{2}}}\,. \)Pro zadané hodnoty: \(\alpha\dot{\,=\,}48^{\circ}\,.\)
Příslušná velikost počáteční rychlosti míče je:
\[v_0^{2}=g\left(\sqrt{(h_1 - h_2)^{2}+L^{2}}+(h_1 - h_2)\right)\,.\]Pro zadané hodnoty:
\[v_0\dot{\,=\,}7{,}7\,\mathrm{m \cdot s^{-1}}\,.\]