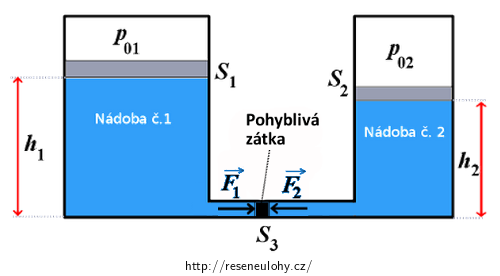
Spojené nádoby
Úloha číslo: 1026
Dvě kapaliny o hustotách 1 000 kg·m−3 a 1 800 kg·m−3 jsou v rovnováze v uzavřených válcových nádobách o průřezech 0,5 m2 a 0,3 m2 spojených krátkou trubicí o průřezu 4·10−4 m2. Nad hladinou kapalin je vzduch, který má v první nádobě tlak 2·105 Pa a v druhé nádobě tlak 1,5·105 Pa. Výška hladiny v první nádobě je 2 m. Ve spojovací trubici je volně pohyblivá zátka zabraňující promísení kapalin. Určete velikost tlakové síly, která působí na zátku zleva a objem kapaliny ve druhé nádobě.
Zápis
ρ1 = 1000 kg·m−3 hustota kapaliny v 1. nádobě ρ2 = 1800 kg·m−3 hustota kapaliny ve 2. nádobě S1 = 0,5 m2 obsah průřezu válcové nádoby č. 1 S2 = 0,3 m2 obsah průřezu válcové nádoby č. 2 S3 = 4·10−4 m2 obsah průřezu spojovací trubice p01 = 2·105 Pa tlak vzduchu nad kapalinou v 1. nádobě p02 = 1,5·105 Pa tlak vzduchu nad kapalinou ve 2. nádobě h1 = 2 m výška hladiny v 1. nádobě F1 = ? velikost tlakové síly působící zleva na zátku V = ? objem kapaliny v nádobě č. 2 Nápověda 1
Při výpočtu tlakové síly na zátku vyjděte z definičního vztahu pro tlak.
Nápověda 2
Předpokládáme, že zátka je - co se týče hloubky - umístěna na dně spojených nádob (zhodnoťte, jak je tento předpoklad nepřesný). Jaký je v takovém případě tlak v místě, kde je zátka umístěna? Uvědomte si, jaké vlivy k této výsledné hodnotě tlaku přispívají.
Nápověda 3
Dosaďte ze vztahu (3) do vztahu (1) a vypočítejte tlakovou sílu na zátku (z levé strany).
Nápověda 4
Nyní určíme objem kapaliny ve druhé nádobě. Objemu jakého tělesa tento objem odpovídá?
Nápověda 5
V zadání se říká, že kapaliny jsou v nádobách v rovnováze. Co to znamená pro pohyb zátky a síly na ni působící? Pomůže vám to k určení výšky/hloubky h2?
Nápověda 6
Velikost síly F1 jste již vypočítali, využijte podobný vztah také pro výpočet síly F2 a dosaďte do vztahu (6). Odtud vyjádřete výšku h2.
Nápověda 7
Dosaďte vyjádřenou výšku ze vztahu (8) do vztahu (5) a dopočítejte objem V.
Celkové řešení
Při výpočtu tlakové síly vyjdeme z definice tlaku. Tlak je definován jako podíl síly působící na danou plochu a obsahu této plochy (v našem případě jde o obsah plochy zátky S3). Odtud vyjádříme tlakovou sílu F1 působící na zátku zleva (tj. v nádobě č. 1):
\[p_1\,=\,\frac{F_1}{S_3}\,\Rightarrow\,F_1\,=\,p_{1}S_{3}\,,\tag{1}\]kde p1 je tlak v místě, kde je umístěna zátka. Tento tlak je určen součtem tlaku vzduchu p01 nad hladinou kapaliny a hydrostatického tlaku ph1 způsobeného vlastní tíhou kapaliny:
\[p_1\,=\,p_{01}\,+\,p_\mathrm{h1}\,.\tag{2}\]Pomocí známého vztahu pro hydrostatický tlak můžeme psát:
\[p_1\,=\,p_{01}\,+\,{h_1}{\rho}_1g\,,\tag{3}\]kde ρ1 je hustota kapaliny v nádobě č. 1 a g tíhové zrychlení.
Poznámka: V naší úvaze jsme umístili zátku na samé dno nádoby č. 1, reálně jsou různé části vertikálně umístěné zátky v různých hloubkách a tlak bychom měli počítat pro hloubku, ve které se nachází střed zátky. Ze zadání je však patrné, že plocha zátky a tedy i její rozměry jsou ve srovnání s ostatními rozměry experimentu velmi malé – pro plochu zátky platí:
\[S_3\,=\,{\pi}r^2\,\Rightarrow\,r\,=\,\sqrt{\frac{S_3}{\pi}}\,=\,\sqrt{\frac{4{\cdot}10^{-4}}{\pi}}\,\mathrm{m}\,\dot=\,1\,\mathrm{cm}\,,\]kde r je poloměr zátky. Hloubka středu zátky a hloubka h1 se tedy liší přibližně o 1 cm, což lze vzhledem k zadané hodnotě h1 = 2 m zanedbat.
Dosazením ze vztahu (3) do vztahu (1) dostáváme:
\[F_1\,=\,(p_{01}\,+\,h_1{\rho}_1g)S_3\,.\tag{4}\]Číselně:
\[F_1\,\dot=\,(2{\cdot}10^5\,+\,2{\cdot}1000{\cdot}9{,}81){\cdot}4{\cdot}10^{-4}\,\mathrm{N}\,\dot=\,88\,\mathrm{N}\,.\]Tlaková síla působící zleva na zátku má velikost přibližně 88 N.
Objem kapaliny ve druhé nádobě určíme jako objem válce:
\[V\,=\,S_2h_2\,.\tag{5}\]Velikost podstavy je zadána, zbývá tedy určit výšku sloupce kapaliny h2 v nádobě č. 2.
(Ze stejných důvodů jako v poznámce výše můžeme zanedbat malý objem kapaliny ve spojovací trubici.)Jsou-li kapaliny v rovnováze, je výška jejich hladin ustálená a nedochází k přesunu kapalin z jedné nádoby do druhé – zátka tedy zůstává v klidu. Síly na ni působící zleva a zprava tedy musí mít stejnou velikost:
\[F_1\,=\,F_2\,.\tag{6}\]Síla F1 je obecně vyjádřena vztahem (4), sílu F2 lze vyjádřit analogicky:
\[F_2\,=\,(p_{02}\,+\,h_2{\rho}_2g)S_3\,.\tag{7}\]Spojením vztahů (4), (6) a (7) dostáváme:
\[(p_{01}\,+\,h_1{\rho}_1g)S_3 = (p_{02}\,+\,h_2{\rho}_2g)S_3\,.\]Úpravou:
\[h_2\,=\,\frac{p_{01}\,-\,p_{02}\,+\,h_1{\rho}_1g}{{\rho}_2g}\,.\tag{8}\]Spojením vztahů (5) a (8) dostáváme:
\[V\,=\,h_2S_2\,=\,\frac{p_{01}\,-\,p_{02}\,+\,h_1{\rho}_1g}{{\rho}_2g}S_2\,.\]Číselně:
\[V\,=\,\frac{2{\cdot}10^5\,-\,1{,}5{\cdot}10^5\,+\,2{\cdot}1000{\cdot}9{,}81}{1800{\cdot}9{,}81}{\cdot}0{,}3\,\mathrm{m^3}\,=\,1{,}18\,\mathrm{m^3}\,.\]Objem kapaliny ve druhé nádobě je přibližně 1,18 m3.
Odpověď
Tlaková síla působící zleva na zátku má velikost přibližně 88 N.
Objem kapaliny ve druhé nádobě je přibližně 1,18 m3.