Sbírka řešených úloh

Vodojem

Úloha číslo: 960

• Zápis

  ph = 0,8 MPa	hydrostatický tlak sloupce vody ve vodojemu
  ph1	hydrostatický tlak sloupce vody mezi přízemím a prvním patrem
  ph3	hydrostatický tlak sloupce vody mezi přízemím a třetím patrem
  h0 = 20 cm = 0,2 m	výška vody v konvici
  h1 = 2,5 m	výška od země k hladině vody v kohoutku v 1. patře
  h3	výška od země k hladině vody v kohoutku ve 3. patře
  hh = ?	výška vody v hubici konvice
  h = ?	výška vodního sloupce ve vodojemu
  pL = ?	tlak vody v kohoutku u Lucky
  pP = ?	tlak vody v kohoutku u Pavla
  Z tabulek:
  g = 10 N/kg	číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu
  ρ = 1000 kg/m3	hustota vody

• Úkol a) – nápověda 1

  Co z fyzikálního hlediska tvoří konvice a její hubice?

• Řešení k nápovědě 1

  Tvoří spojené nádoby.

• Úkol a) – nápověda 2

  Co můžeme říct o hladině vody ve spojených nádobách?

• Řešení k nápovědě 2

  Po naplnění spojených nádob vodou vystoupí hladina vody v obou nádobách do stejné výšky.

  

• Úkol a) – nápověda 3

  Na základě předchozích úvah zformulujte odpověď.

• Řešení k nápovědě 3

  Protože konvice a její hubice tvoří spojené nádoby, vystoupí voda v hubici do stejné výšky jako v těle konvice. Voda v hubici je ve výšce 20 cm ode dna konvice.

• Úkol b) – nápověda 1

  Co z fyzikálního hlediska tvoří vodojem a vodovodní rozvod v panelovém domě?

• Řešení k nápovědě 1

  Tvoří spojené nádoby.

• Úkol b) – nápověda 2

  Úkol vodojemu je zajistit potřebný tlak ve vodovodním rozvodu. Jaký druh tlaku vodojem zajišťuje?

• Řešení k nápovědě 2

  Jde o hydrostatický tlak sloupce vody, která se ve vodojemu nachází. Je to tlak, kterým kapalina tlačí na dno a stěny nádoby, ve které se nachází, na tělesa ponořená do této kapaliny a na své vlastní části (výše položené části kapaliny tlačí na ty níže položené).

• Úkol b) – nápověda 3

  Na čem závisí hydrostatický tlak? Jak ho vypočítáme?

• Řešení k nápovědě 3

  Hydrostatický tlak vypočítáme jako:

  $$p_\mathrm{h}\,=\,h{\rho}g\,,\tag{1}$$

  kde h je hloubka pod povrchem hladiny (v našem případě výška vodního sloupce ve vodojemu), ρ je hustota kapaliny a g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu).

  

• Úkol b) – nápověda 4

  Které veličiny ve vzorci (1) známe a co chceme vypočítat?

• Řešení k nápovědě 4

  Chceme vypočítat výšku h vody ve vodojemu, ostatní veličiny známe.

• Úkol b) – nápověda 5

  Vyjádřete neznámou veličinu ze vzorce (1) a vypočítejte ji.

• Řešení k nápovědě 5

  Neznámá výška vody ve vodojemu se vypočítá:

  $$h\,=\,\frac{p_\mathrm{h}}{{\rho}{\cdot}g}\,,\tag{2}$$

  kde p_h = 0,8 MPa je hydrostatický tlak vody u dna vodojemu, ${\rho}$ je hustota kapaliny (v našem případě vody) a g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu).

  Číselně:

  $$h\,=\,(\frac{800 000}{1000{\cdot}10})\,\mathrm{m}\,=\,80\,\mathrm{m}\,.$$

• Úkol c) – nápověda 1

  Vodojem a vodovodní rozvod v panelovém domě fungují také jako spojené nádoby. Oproti části a) je zde ale rozdíl. Situace je znázorněna na obrázku.

  

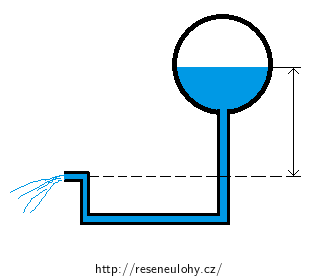
  V čem jsou tyto spojené nádoby rozdílné oproti konvici z a)?

• Řešení k nápovědě 1

  „Nádoba“ vlevo (kohoutek s částí potrubí) je nižší než „nádoba“ vpravo (vodojem s částí potrubí).

• Úkol c) – nápověda 2

  Z části b) už víme, že hydrostatický tlak, který vodojem vytváří v přízemí domu, je úměrný výšce vodního sloupce ve vodojemu.

  Jak vysoko by musela sahat voda v pravé „nádobě“, aby byl hydrostatický tlak tohoto sloupce vody stejný jako hydrostatický tlak sloupce vody v levé „nádobě“?

• Řešení k nápovědě 2

  Ze vzorce (1) je vidět, že aby byly hydrostatické tlaky sloupců vody stejné, voda v pravé nádobě by musela sahat do stejné výšky jako v levé. (Představit si to vám může pomoct přerušovaná čára na obrázku. Kdyby napravo nebyla nad přerušovanou čarou už žádná voda, tak by vlevo voda nevytékala.)

• Úkol c) – nápověda 3

  Čím je dán tlak vody u Lucky v prvním patře?

• Řešení k nápovědě 3

  Je dán rozdílem hydrostatických tlaků p_h – p_h1, kde p_h je hydrostatický tlak sloupce vody mezi přízemím a hladinou ve vodojemu a p_h1 je hydrostatický tlak sloupce vody mezi přízemím a prvním patrem.

• Úkol c) – nápověda 4

  Vypočítejte tento tlak.

• Řešení k nápovědě 4

  Tlak vody u Lucky spočítáme:

  $$p_\mathrm{L}\,=\,p_\mathrm{h}\,-\,p_\mathrm{h_1}\,,$$

  $$p_\mathrm{L}\,=\,p_\mathrm{h}\,-\,h_1\cdot\rho\cdot g\,,$$

  kde p_h je hydrostatický tlak vody ve vodojemu, h₁ je výška od země k hladině vody v kohoutku v 1. patře.

  Číselně:

  $$p_\mathrm{L}\,=\,({800000-2{,}5{\cdot}1000\cdot10})\mathrm{Pa}\,=\,775000\mathrm{Pa}\,=\,775\mathrm{kPa}\,.$$

• Úkol c) – nápověda 5

  Čím je dán tlak vody u Pavla ve třetím patře?

• Řešení k nápovědě 5

  Je dán rozdílem hydrostatických tlaků p_h – p_h3, kde p_h je hydrostatický tlak sloupce vody mezi přízemím a hladinou vody ve vodojemu a p_h3 je hydrostatický tlak sloupce vody mezi přízemím a třetím patrem.

• Úkol c) – nápověda 6

  Vypočtěte tento tlak.

• Řešení k nápovědě 6

  Tlak vody u Pavla spočítáme:

  $$p_\mathrm{P}\,=\,p_\mathrm{h}\,-\,p_\mathrm{h_3}\,,$$

  $$p_\mathrm{P}\,=\,p_\mathrm{h}\,-\,h_3\cdot\rho\cdot g\,,$$

  kde p_h je hydrostatický tlak vody ve vodojemu, h₃ je výška od země k hladině vody v kohoutku ve 3. patře.

  Číselně:

  $$p_\mathrm{P}\,=\,({800000-3{\cdot}2{,}5{\cdot}1000\cdot10})\mathrm{Pa}\,=\,725000\mathrm{Pa}=\,725\mathrm{kPa}\,.$$

• Celkové řešení

  Řešení části a):

  Protože konvice a její hubice tvoří spojené nádoby, vystoupí voda v hubici do stejné výšky jako v těle konvice. Voda v hubici je ve výšce 20 cm ode dna konvice.

  

  Řešení části b):

  Výšku vody ve vodojemu vypočítáme z tlaku, který tato voda vytváří v přízemí panelového domu. Je to tlak, kterým kapalina tlačí na dno a stěny nádoby, ve které se nachází, na tělesa ponořená do této kapaliny a na své vlastní části (výše položené části kapaliny tlačí na ty níže položené).

  Tento takzvaný hydrostatický tlak je určen vztahem:

  $$p_\mathrm{h}\,=\,h{\rho}g\,,\tag{1}$$

  kde h je hloubka pod povrchem hladiny (v našem případě výška vodního sloupce ve vodojemu), ρ je hustota kapaliny a g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu).

  

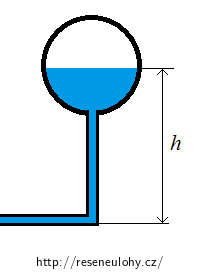
  Výška vody ve vodojemu se tedy vypočítá:

  $$h\,=\,\frac{p_\mathrm{h}}{{\rho}{\cdot}g}\,,\tag{2}$$

  kde p_h = 0,8 MPa je právě hydrostatický tlak vody ve vodojemu.

  $$h\,=\,(\frac{800 000}{1000{\cdot}10})\,\mathrm{m}\,=\,80\,\mathrm{m}$$

  Řešení části c):

  Tlak vody u Lucky je dán rozdílem hydrostatických tlaků p_h – p_h1, kde p_h je hydrostatický tlak sloupce vody mezi přízemím a hladinou vody ve vodojemu a p_h1 je hydrostatický tlak sloupce vody mezi přízemím a prvním patrem. Spočítáme jej jako:

  $$p_\mathrm{L}\,=\,p_\mathrm{h}\,-\,p_\mathrm{h_1}\,,$$

  $$p_\mathrm{L}\,=\,p_\mathrm{h}\,-\,h_1\cdot\rho\cdot g\,,$$

  kde p_h je hydrostatický tlak vody ve vodojemu, h₁ je výška od země k hladině vody v kohoutku v 1. patře.

  Číselně:

  $$p_\mathrm{L}\,=\,({800000-2{,}5{\cdot}1000\cdot10})\mathrm{Pa}\,=\,775000\mathrm{Pa}\,=\,775\mathrm{kPa}\,.$$

  Tlak vody u Pavla je dán rozdílem hydrostatických tlaků p_h – p_h3, kde p_h je hydrostatický tlak sloupce vody mezi přízemím a hladinou vody ve vodojemu a p_h3 je hydrostatický tlak sloupce vody mezi přízemím a třetím patrem. Spočítáme jej jako:

  $$p_\mathrm{P}\,=\,p_\mathrm{h}\,-\,p_\mathrm{h_3}\,,$$

  $$p_\mathrm{P}\,=\,p_\mathrm{h}\,-\,h_3\cdot\rho\cdot g\,,$$

  kde p_h je hydrostatický tlak vody ve vodojemu, h₃ je výška od země k hladině vody v kohoutku ve 3. patře.

  Číselně:

  $$p_\mathrm{P}\,=\,({800000-3{\cdot}2{,}5{\cdot}1000\cdot10})\mathrm{Pa}\,=\,725000\mathrm{Pa}=\,725\mathrm{kPa}\,.$$

• Odpověď

  a)

  h_h = 20 cm

  Hladina vody v hubici konvice je ve výšce 20 cm ode dna konvice.

  b)

  $$h\,=\,\frac{p_\mathrm{h}}{{\rho}{\cdot}g} \,=\,80\,\mathrm{m}$$

  Hladina vody ve vodojemu je ve výšce 80 m nad zemí.

  c)

  $$p_\mathrm{L}\,=\,p_\mathrm{h}\,-\,h_1\cdot\rho\cdot g = \,=\,775\mathrm{kPa}$$ $$p_\mathrm{P}\,=\,p_\mathrm{h}\,-\,h_3\cdot\rho\cdot g = \,=\,725\mathrm{kPa}$$

  Tlak vody v kohoutku u Lucky je 775 kPa a v kohoutku u Pavla je tlak vody 725 kPa.