Obvodová rychlost na Zemi
Úloha číslo: 194
Jaká je obvodová rychlost bodu během denní rotace Země, jestliže bod je:
a) na zemském rovníku,
b) na 50 ° severní šířky.
Zápis
T = 23 h 56 min 4 s siderická doba rotace Země R = 6378 km poloměr Země α = 50 ° severní šířka vR = ? obvodová rychlost na rovníku v50 = ? obvodová rychlost na 50 ° s. š. Nápověda 1
Rozmyslete si, která fyzikální veličina popisující otáčivý pohyb je vhodná pro vyjádření obvodové rychlosti.
Nápověda 2: Úhlová rychlost, vzdálenost bodu od osy otáčení
Pomocí vhodného vztahu spočítejte úhlovou rychlost.
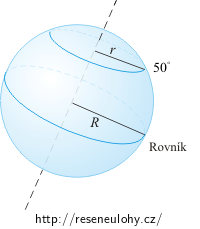
Za pomoci obrázku určete kolmé vzdálenosti bodu na rovníku a bodu na 50 ° s. š. od osy otáčení.
Celkové řešení
Obvodovou rychlost určíme pomocí úhlové rychlosti ω, jejíž velikost nezávisí na vzdálenosti otáčejícího se bodu od osy otáčení. Pro velikost obvodové rychlosti platí v = ωr, kde r je kolmá vzdálenost bodu od osy otáčení.
Úhlová rychlost
Pro úhlovou rychlost rotace Země platí:
\[\omega = \frac{2\pi}{T},\] \[T = 23 \mathrm{h}\,56 \mathrm{min}\, 4 \mathrm{s} = 86164\, \mathrm{s},\] \[\omega = \frac{2\pi}{86164}\, \mathrm{s^{-1}} \dot{=} 7{,}292{\cdot} 10^{-5} \, \mathrm{s^{-1}}.\]Kolmé vzdálenosti
Kolmá vzdálenost bodu na rovníku od osy otáčení je rovna poloměru Země.
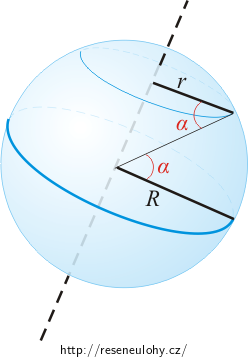
Kolmou vzdálenost bodu na 50 ° s. š. určíme pomocí následujícího obrázku.
Na obrázku vidíme, že hledaná vzdálenost r je odvěsna pravoúhlého trojúhelníku s přeponou délky poloměru Země R. Platí tedy:
\[r = R\cos\alpha = 6378 \, \mathrm{km} \cdot \cos 50^{\circ} \dot{=}\, 4099 \, \mathrm{km}.\]Obvodové rychlosti
Nyní již stačí dosadit získané hodnoty do rovnice pro obvodovou rychlost.
a) \[v_\mathrm{R} = \omega R \dot{=} 7{,}292 {\cdot} 10^{-5}\cdot 6378\, \mathrm{km \cdot s^{-1}} \dot{=} 0{,}465\, \mathrm{km \cdot s^{-1}} \dot{=}\, 465\,\mathrm{m \cdot s^{-1}}\]
b) \[v_{50} = \omega r = \frac{v_\mathrm{R}}{R} R\cos\alpha = v_\mathrm{R}\cos\alpha \dot{=} 465 \cdot \cos 50^{\circ} \,\mathrm{m \cdot s^{-1}}\dot{=}\, 299\,\mathrm{m \cdot s^{-1}}\]
Poznámka:
Siderická doba rotace je doba jednoho otočení Země okolo své osy vůči vzdáleným hvězdám. Tato doba je 23 h 56 min 4 s.
Pokud za periodu rotace Země dosadíme 24 h, dostaneme chybu v úhlové rychlosti na druhém desetinném místě, tedy přibližně 7,272·10−5 s−1.
Výsledná rychlost pak je přibližně v případě a) 464 m·s−1 a v případě b) 298 m·s−1.
Odpověď
Obvodová rychlost bodu na rovníku je přibližně 465 m·s−1 a bodu na 50 ° s. š. je asi 299 m·s−1.