Auto a konstantní brzdná síla
Úloha číslo: 44
Auto o hmotnosti m se pohybuje po vodorovné silnici rovnoměrně přímočaře rychlostí o velikosti v0. V čase t = 0 s na něj začala působit proti směru pohybu konstantní brzdná síla Fb. Předpokládejte, že v čase t = 0 s byla souřadnice x = 0 m.
1) Určete, jak se s časem mění velikost rychlosti v(t) a souřadnice auta x(t).
2) Určete čas tz, za který se auto zastaví, a dráhu xz, kterou přitom urazí.

Poznámka: Místo velikost rychlosti píšeme dále jen rychlost.
Zápis
m hmotnost auta v0 počáteční rychlost auta Fb konstantní brzdná síla v(t) = ? průběh rychlosti auta x(t) = ? průběh souřadnice auta tz = ? čas zastavení auta xz = ? dráha zastavení auta Nápověda 1 - síly působící na auto, pohybová rovnice
Uvědomte si, jaké síly působí na auto, a napište pro něj pohybovou rovnici.
Nápověda 2 - zrychlení auta, průběh v(t), x(t)
Vyjádřete zrychlení auta a zjistěte nejprve průběh rychlosti a poté průběh souřadnice.
Nápověda 3 - čas a dráha zastavení
Uvědomte si, jaká bude rychlost v okamžiku zastavení, a využijte tento údaj k určení času zastavení. Znáte-li průběh x(t) a čas zastavení, dráhu zastavení již snadno určíte.
Poznámka
Dráha zastavení by se dala určit i ze zákona zachování energie.
Počáteční kinetická energie auta je rovna práci brzdné síly působící na dráze zastavení:
\[\frac{mv_0^2}{2}\,=\,F_\mathrm{b}x_\mathrm{z}.\]Odtud:
\[x_\mathrm{z}\,=\,\frac{mv_0^2}{2F_\mathrm{b}}.\]CELKOVÉ ŘEŠENÍ
Nejprve si rozmyslíme, jaké síly působí na auto a napíšeme pro něj pohybovou rovnici.
Na auto působí následující síly:
\(\vec{F}_\mathrm{b}\)…brzdná síla
\(\vec{F}_\mathrm{G}\)…tíhová síla
\(\vec{N}\)…normálová síla, kterou na auto působí podložka
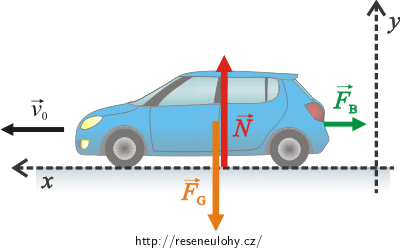
Poznámka: Síla podložky N působí na kola auta, do obrázku kreslíme výslednici těchto sil.
Pohybová rovnice pro auto je:
\[\vec{F}_\mathrm{b}+\vec{F}_\mathrm{G}+\vec{N}= m\vec{a}.\tag{1}\]
Rovnici (1) přepíšeme skalárně:
\[ x : -F_\mathrm{b} \,=\, ma,\tag{2}\] \[ y : N - F_\mathrm{G} \,=\, 0.\tag{3}\]Poznámka: Z obrázku můžete vidět, proč je v rovnici (2) znaménko mínus. Brzdná síla působí proti směru pohybu auta. Síly \(\vec{F}_\mathrm{G}\) a \(\vec{N}\) jsou kolmé na brzdnou sílu \(\vec{F}_\mathrm{b}\), jsou stejně veliké opačného směru a jejich výslednice je nulová. Zrychlení je ve směru osy y nulové.
Zrychlení auta:
Ze vztahu (2) pro zrychlení dostáváme:
\[a \,=\,-\frac{F_\mathrm{b}}{m}.\tag{4}\]Zrychlení auta je konstantní. Jelikož auto vlivem brzdné síly Fb zpomaluje, zrychlení je záporné.
Průběh v(t):
Integrací zrychlení ze vztahu (4) získáme závislost rychlosti na čase:
\[v(t)=\int{a}\,\mathrm{d}t\,=\,\int{-\frac{F_\mathrm{b}}{m}}\,\mathrm{d}t\,=\,-{\frac{F_\mathrm{b}}{m}}t+K.\tag{5}\]K je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla rychlost v = v0. Dosadíme-li t = 0 s do vztahu (5), pak musí platit:
v0 = 0 + K.
A tedy:
v0 = K.
Přepíšeme-li rovnici (5), získáme závislost rychlosti auta na čase:
\[v(t)=-{\frac{F_\mathrm{b}}{m}}t+v_0.\tag{6}\]Průběh x(t):
Integrací rychlosti ze vztahu (6) získáme závislost souřadnice na čase:
\[x(t)\,=\,\int{v(t)}\,\mathrm{d}t\,=\,\int{(-\frac{F_\mathrm{b}}{m}}t+v_0)\,\mathrm{d}t\,=\,-{\frac{F_\mathrm{b}}{2m}}t^2+v_0t+C.\tag{7}\]C je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla souřadnice x = 0. Dosadíme-li t = 0 s do vztahu (7), pak musí platit:
0 = 0 + C.
A tedy:
C = 0.
Přepíšeme-li rovnici (7), získáme závislost souřadnice auta na čase:
\[x\left(t\right)\,=\,-{\frac{F_\mathrm{b}}{2m}}t^2+v_0t.\tag{8}\]Čas zastavení tz:
V okamžiku zastavení bude rychlost nulová. Dosazením do vztahu (6) tak pro čas zastavení dostaneme:
\[0\,=\,-{\frac{F_\mathrm{b}}{m}}t_\mathrm{z}+v_0.\]Odtud:
\[t_\mathrm{z}\,=\,\frac{mv_0}{F_\mathrm{b}}.\tag{9}\]Dráha zastavení xz:
Dráhu zastavení dostaneme dosazením vztahu (9) pro čas zastavení do vztahu pro závislost souřadnice na čase (8):
\[x_\mathrm{z}\,=\,-{\frac{F_\mathrm{b}}{2m}}t_\mathrm{z}^2+v_0t_\mathrm{z} \,=\,-{\frac{F_\mathrm{b}}{2m}}\left(\frac{mv_0}{F_\mathrm{b}}\right)^2+v_0\left(\frac{mv_0}{F_\mathrm{b}}\right),\] \[x_\mathrm{z}\,=\,\frac{mv_0^2}{2F_\mathrm{b}}.\tag{10}\]CELKOVÁ ODPOVĚĎ
Průběh velikosti rychlosti auta je \(v\left(t\right)\,=\,-{\frac{F_\mathrm{b}}{m}}t+v_0\).
Průběh souřadnice auta je \(x\left(t\right)\,=\,-{\frac{F_\mathrm{b}}{2m}}t^2+v_0t\).
Čas zastavení auta je \(t_\mathrm{z}\,=\,\frac{mv_0}{F_\mathrm{b}}\).
Dráha zastavení auta je \(x_\mathrm{z}\,=\,\frac{mv_0^2}{2F_\mathrm{b}}\).



