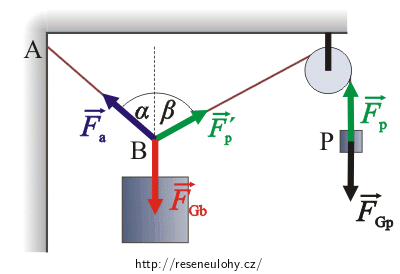
Závaží na laně
Úloha číslo: 521
Zápis
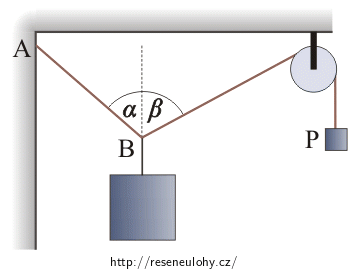
mb = 10 kg hmotnost závaží B α = 45° požadovaný úhel svíraný lanem AB se svislicí β = 60° požadovaný úhel svíraný lanem mezi bodem B a kladkou se svislicí mp =? (kg) hmotnost závaží P Fa =? (N) namáhání lana AB Nápověda 1
Nakreslete si do obrázku všechny síly působící na závaží B a na závaží P. Co musí platit pro jejich výslednice?Nápověda 2
Zvolte vhodně soustavu souřadnic a přepište rovnice (1) a (2) skalárně. Ze získaných rovnic vyjádřete hledané veličiny.
Celkové řešení
Do obrázku nakreslíme všechny síly působící na závaží B a na závaží P a zvolíme soustavu souřadnic.
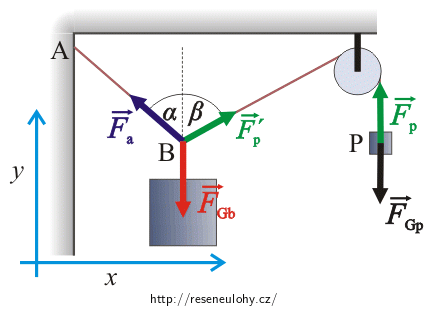
Závaží P:
\(\vec{F}_\mathrm{Gp}\) ....... tíhová síla (FGp = mpg)
\(\vec{F}_\mathrm{p}\) ....... síla, kterou táhne lano
Závaží B:
-
\(\vec{F}_\mathrm{Gb}\) ....... tíhová síla (FGb = mbg)
-
\(\vec{F^,}_\mathrm{p}\) ....... síla, kterou táhne lano, na kterém je závaží P
(kladka je v klidu, takže pro velikost sil \(\vec{F}_\mathrm{p}\) a \(\vec{F^,}_\mathrm{p}\) platí, že Fp = F´p, závaží P táhne prostřednictvím lana za závaží B a naopak)
-
\(\vec{F}_\mathrm{a}\) ....... síla, kterou táhne lano upevněné na stěně
Obě závaží jsou v klidu, takže musí platit, že výslednice sil, které na ně působí, jsou rovny nulovému vektoru.
Závaží P:
\[\vec{F}_\mathrm{Gp}+\vec{F}_\mathrm{p}=\vec{0}\,.\tag{1}\]Závaží B:
\[\vec{F}_\mathrm{Gb}+\vec{F'}_\mathrm{p}+\vec{F}_\mathrm{a}=\vec{0}\,.\tag{2}\]Rovnice (1), (2) přepíšeme skalárně:
Závaží P:
\[{F}_\mathrm{p}=F_\mathrm{Gp}=m_\mathrm{p}g\,.\]
Závaží B:
\[x:\hspace{60px}F_\mathrm{p}\sin\beta-F_\mathrm{a}\sin\alpha=0,\tag{3}\]
\[y:\hspace{10px}F_\mathrm{a}\cos\alpha+F_\mathrm{p}\cos\beta-F_\mathrm{Gb}=0.\tag{4}\]
Z rovnice (3):
\[F_\mathrm{a} = F_\mathrm{p} \frac{\sin \beta}{\sin \alpha}\,.\tag{5}\]Dosadíme do rovnice (4):
\[F_\mathrm{p} \frac{\sin \beta}{\sin \alpha} \cos \alpha + F_\mathrm{p} \cos \beta = F_\mathrm{Gb}\,.\]A upravíme:
\[F_\mathrm{p}\frac{\sin\beta\cos\alpha+\sin\alpha\cos \beta}{\sin \alpha} = F_\mathrm{Gb}\,.\]S použitím vztahu pro sinus součtu úhlů:
\[F_\mathrm{p}\sin(\alpha+\beta)=F_\mathrm{Gb}\sin\alpha\,,\] \[F_\mathrm{p}=F_\mathrm{Gb}\frac{\sin\alpha}{\sin(\alpha+\beta)}\,.\]Tedy:
\[gm_\mathrm{p}=gm_\mathrm{b}\frac{\sin\alpha}{\sin(\alpha+\beta)}\,,\] \[m_\mathrm{p}=m_\mathrm{b}\frac{\sin\alpha}{\sin(\alpha+\beta)}\,.\]Dosadíme získané Fp do rovnice (5):
\[F_\mathrm{a} = F_\mathrm{Gb} \frac{\sin \alpha}{\sin (\alpha + \beta)} \frac{\sin \beta}{\sin \alpha}\,,\] \[F_\mathrm{a} = F_\mathrm{Gb} \frac{\sin \beta}{\sin (\alpha + \beta)}\,,\] \[F_\mathrm{a} = gm_\mathrm{b} \frac{\sin \beta}{\sin (\alpha + \beta)}\,.\]Dosadíme zadané hodnoty:
α, β, mb:
\[m_\mathrm{p}=10\frac {\sin45^\circ}{\sin(45^\circ+60^\circ)}\,\mathrm{kg}\dot{=}7{,}3 \,\mathrm{kg}\,,\] \[F_\mathrm{a}=10{\cdot}10\frac {\sin60^\circ}{\sin(45^\circ+60^\circ)}\,\mathrm{N} \dot{=} 90 \,\mathrm{N}\,.\]Odpověď
Hledaná hmotnost závaží P je rovna:
\[m_\mathrm{p}=m_\mathrm{b}\frac{\sin\alpha}{\sin(\alpha+\beta)}\,.\]Namáhání lana AB je rovno:
\[F_\mathrm{a} = gm_\mathrm{b} \frac{\sin \beta}{\sin (\alpha + \beta)} \,.\]Číselně:
\[m_\mathrm{p} \dot{=}7{,}3 \,\mathrm{kg}\,,\] \[F_\mathrm{a} \dot{=} 90 \,\mathrm{N}\,.\]