Těžiště homogenního rotačního kužele

Úloha číslo: 1127

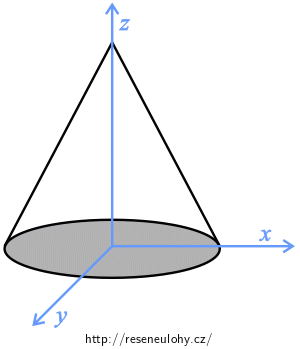
Určete polohu těžiště přímého homogenního rotačního kužele o poloměru podstavy R a výšce v.

Nápověda 1
Zamyslete se nad tím, co vlastně znamená úkol „určete polohu těžiště“. Co má být výstupem úlohy, co vlastně určujete?
Řešení nápovědy 1
Určit polohu těžiště znamená určit souřadnice těžiště v nějakém vhodně zvoleném souřadném systému. Výstupem jsou tedy tři souřadnice těžiště T: x_T, y_T, z_T.
Nápověda 2
Vhodně umístěte kužel do souřadného systému. Lze jeho polohu zvolit tak, aby se další výpočty zjednodušily? (Nelze vybrat souřadný systém takovým způsobem, aby některé souřadnice nebylo nutné vůbec počítat?)
Řešení nápovědy 2
Velmi výhodné umístění kužele do souřadného systému ukazuje obrázek níže. Kruhová podstava kužele leží v rovině xy, osa z je na tuto rovinu kolmá a prochází středem podstavy i vrcholem kužele.

Protože takto umístěný útvar je rotačně symetrický kolem osy z, musí jeho těžiště ležet na této ose – libovolný bod na ose z má ovšem nulovou x-ovou i y-ovou souřadnici, tedy ihned můžeme psát:
\[x_\mathrm{T}\,=\,y_\mathrm{T}\,=\,0.\]
Dále tedy stačí vypočítat pouze z-ovou souřadnici těžiště z_T.
Nápověda 3
Jak je obecně definován vztah pro výpočet polohového vektoru r_T, který určuje polohu těžiště?
Řešení nápovědy 3
Polohový vektor r_T určující polohu těžiště daného objektu lze určit jako:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\tag{1}\]
Nápověda 4
Kužel v zadání úlohy výše je homogenní. Využijte toho k tomu, abyste od hmotnostních elementů ve vztahu (1) přešli k elementům objemovým.
Řešení nápovědy 4
Element hmotnosti dm lze pro homogenní kužel rozepsat jako součin:

\[dm\,=\,{\rho}dV,\]

kde ρ je hustota materiálu a dV je element objemu. Pak platí:
\[\vec{r}_\mathrm{T}\,=\,\frac{{\rho}\int{\vec{r}}dV}{{\rho}{\int}dV}\,=\,\frac{\int{\vec{r}}dV}{{\int}dV}.\]
Výraz ve jmenovateli představuje vysčítání všech objemových elementů, kterými je kužel tvořen – dostáváme zde tedy celkový objem kužele V:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dV}{V}.\tag{2}\]
Nápověda 5
Jak se změní vztah (2), pokud se budeme (dle počáteční úvahy) zabývat pouze z-ovou souřadnicí těžiště z_T?
Řešení nápovědy 5
Protože souřadnice polohového vektoru r_T se ve vztazích (1) i (2) počítají po složkách, lze jednoduše pro z-ovou souřadnici psát:
\[z_\mathrm{T}\,=\,\frac{\int{z}dV}{V}.\tag{3}\]
Nápověda 6
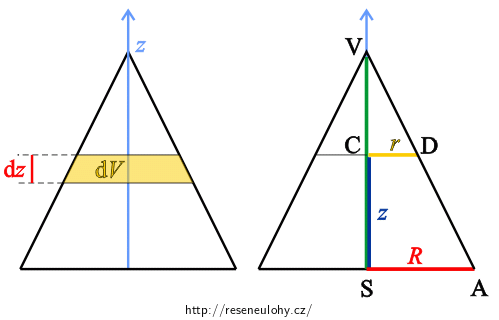
Integrál ve vztahu (3) je trojný a jako takový ho lze řešit (viz Alternativní řešení). Vhodnou volbou objemového elementu dV lze ale tento integrál převést na jednorozměrný. Kužel rozdělíme vodorovnými řezy na „placky“ o výšce dz a proměnném poloměru podstavy r – při malé výšce dz je můžeme považovat za válečky. Nakreslete si obrázek takto rozděleného kužele ve svislém řezu a vyjádřete z něj objemový element dV pouze pomocí proměnné z a konstant (R, v). Užitečná pro vás bude například podobnost trojúhelníků.
Řešení nápovědy 6

Z obrázku výše je patrné, že pro dostatečně malé dz platí:
\[dV\,=\,{\pi}r^2dz.\tag{4}\]
Přitom z podobnosti trojúhelníků VSA a VCD platí:
\[\frac{r}{R}\,=\,\frac{v\,-\,z}{v}\,\Rightarrow\,r\,=\,R\frac{v\,-\,z}{v}.\tag{5}\]
Dosazením z rovnic (4) a (5) do vztahu (3) dostáváme:
\[z_\mathrm{T}\,=\,\frac{\int{z}{\pi}(R\frac{v\,-\,z}{v})^2dz}{V}.\]
Doplnit můžeme ještě objem kužele V, který je V = πR²v/3:
\[z_\mathrm{T}\,=\,\frac{3\int{z}{\pi}(R\frac{v\,-\,z}{v})^2dz}{{\pi}R^2v}\,=\,\frac{3}{v^3}\int{z(v-z)^2dz}.\tag{6}\]
Nápověda 7
Nyní již doplňte ve vztahu (6) pouze integrační meze a integrál dopočítejte.
Řešení nápovědy 7
Abychom vyčerpali celý objem kužele, budeme integrovat od z = 0 do z = v:
\[z_\mathrm{T}\,=\,\frac{3}{v^3}\int_0^v{z(v^2\,-\,2vz\,+\,z^2)dz}\,=\,\frac{3}{v^3}\int_0^v{(zv^2\,-\,2vz^2\,+\,z^3)dz},\] \[z_\mathrm{T}\,=\,\frac{3}{v^3}[\frac{1}{2}z^2v^2\,-\,\frac{2}{3}vz^3\,+\,\frac{1}{4}z^4]_0^v\,=\,\frac{3}{v^3}(\frac{1}{2}v^4\,-\,\frac{2}{3}v^4\,+\,\frac{1}{4}z^4),\] \[z_\mathrm{T}\,=\,\frac{3}{v^3}{\cdot}\frac{1}{12}v^4\,=\,\frac{v}{4}.\]
Těžiště kužele má tedy z-ovou souřadnici z_T = v/4.
Celkové řešení
Určit polohu těžiště znamená určit souřadnice těžiště v nějakém vhodně zvoleném souřadném systému. Výstupem jsou tři souřadnice těžiště T: x_T, y_T, z_T.

Velmi výhodné umístění kužele do souřadného systému ukazuje obrázek níže. Kruhová podstava kužele leží v rovině xy, osa z je na tuto rovinu kolmá a prochází středem podstavy i vrcholem kužele.

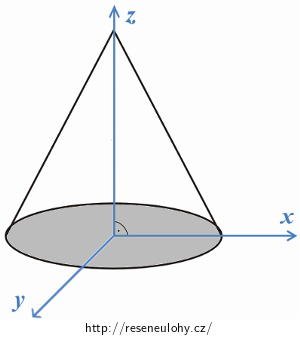
Protože takto umístěný útvar je rotačně symetrický kolem osy z, musí jeho těžiště ležet na této ose – libovolný bod na ose z má ovšem nulovou x-ovou i y-ovou souřadnici, tedy ihned můžeme psát:
\[x_\mathrm{T}\,=\,y_\mathrm{T}\,=\,0.\]
Dále stačí vypočítat pouze z-ovou souřadnici těžiště z_T.

Polohový vektor r_T určující polohu těžiště daného objektu lze určit jako:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dm}{{\int}dm}.\tag{1}\]
Element hmotnosti dm lze pro homogenní kužel rozepsat jako součin:

\[dm\,=\,{\rho}dV,\]

kde ρ je hustota materiálu a dV je element objemu. Pak platí:
\[\vec{r}_\mathrm{T}\,=\,\frac{{\rho}\int{\vec{r}}dV}{{\rho}{\int}dV}\,=\,\frac{\int{\vec{r}}dV}{{\int}dV}.\]
Výraz ve jmenovateli představuje vysčítání všech objemových elementů, kterými je kužel tvořen – dostáváme zde tedy celkový objem kužele V:
\[\vec{r}_\mathrm{T}\,=\,\frac{\int{\vec{r}}dV}{V}.\tag{2}\]
Protože souřadnice polohového vektoru r_T se ve vztazích (1) i (2) počítají po složkách, lze jednoduše pro z-ovou souřadnici psát:
\[z_\mathrm{T}\,=\,\frac{\int{z}dV}{V}.\tag{3}\]
Pro převedení trojného integrálu ve vztahu (3) na integrál jednorozměrný si celý kužel rozdělíme vodorovnými řezy na soustavu „skoro“ válečků výšky dz a proměnného poloměru podstavy r (viz obrázek).

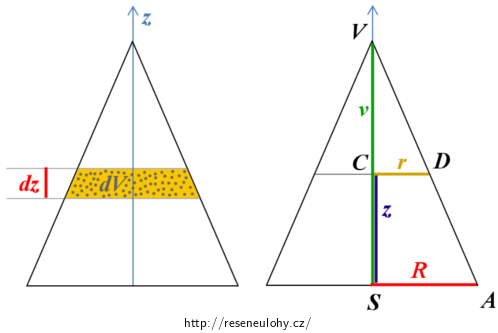
Z obrázku výše je patrné, že pro dostatečně malá dz platí:
\[dV\,=\,{\pi}r^2dz.\tag{4}\]
Přitom z podobnosti trojúhelníků VSA a VCD platí:
\[\frac{r}{R}\,=\,\frac{v\,-\,z}{v}\,\Rightarrow\,r\,=\,R\frac{v\,-\,z}{v}.\tag{5}\]
Dosazením z rovnic (4) a (5) do vztahu (3) dostáváme:
\[z_\mathrm{T}\,=\,\frac{\int{z}{\pi}(R\frac{v\,-\,z}{v})^2dz}{V}.\]
Doplnit můžeme ještě objem kužele V, který je V = πR²v/3:
\[z_\mathrm{T}\,=\,\frac{3\int{z}{\pi}(R\frac{v\,-\,z}{v})^2dz}{{\pi}R^2v}\,=\,\frac{3}{v^3}\int{z(v-z)^2dz}.\tag{6}\]
Abychom vyčerpali celý objem kužele, budeme integrovat od z = 0 do z = v:
\[z_\mathrm{T}\,=\,\frac{3}{v^3}\int_0^v{z(v^2\,-\,2vz\,+\,z^2)dz}\,=\,\frac{3}{v^3}\int_0^v{(zv^2\,-\,2vz^2\,+\,z^3)dz},\] \[z_\mathrm{T}\,=\,\frac{3}{v^3}[\frac{1}{2}z^2v^2\,-\,\frac{2}{3}vz^3\,+\,\frac{1}{4}z^4]_0^v\,=\,\frac{3}{v^3}(\frac{1}{2}v^4\,-\,\frac{2}{3}v^4\,+\,\frac{1}{4}z^4),\] \[z_\mathrm{T}\,=\,\frac{3}{v^3}{\cdot}\frac{1}{12}v^4\,=\,\frac{v}{4}.\]
Těžiště kužele má tedy z-ovou souřadnici z_T = v/4.
Alternativní řešení
Ukážeme si ještě jiné možné řešení úlohy, spočívající v jiném matematickém přístupu. Úvodní úvahy jsou zcela stejné jako ve výše uvedeném postupu, liší se ale výpočet integrálu ve vztahu (3).

Tento trojný integrál si přepíšeme do válcových (cylindrických) souřadnic, jejichž počátek je identický s počátkem našeho kartézského systému. Připomeňme si převod kartézských souřadnic na válcové:
\[x\,=\,r\cos{\varphi},\] \[y\,=\,r\sin{\varphi},\] \[z\,=\,z.\tag{7}\]
Protože v integrálu ve vztahu (3) se objevuje pouze proměnná z, využijeme pouze poslední ze vztahů výše, který navíc tvar integrálu nemění.
Dále rozepíšeme objemový element dV ve válcových souřadnicích: \[dV\,=\,rdrdzd{\varphi}.\tag{8}\]
Jde v podstatě o plošný element v polárních souřadnicích (viz alternativní řešení úlohy Těžiště čtvrtkruhu) přenásobený „výškou“ dz.

Vztahy (7) a (8) dosadíme do rovnice (3), stejně jako objem kužele V:
\[z_\mathrm{T}\,=\,\frac{\int{zdV}}{V}\,=\,\frac{\int\int\int{zrdrdzd\varphi}}{\frac{{\pi}R^2v}{3}}\,=\,\frac{3}{{\pi}R^2v}\int\int\int{zrdrdzd\varphi}.\]
Zvýšenou pozornost budeme věnovat určení integračních mezí. Nejsnadnější situace je v proměnné φ, kde budeme integrovat od φ = 0 do φ = 2π. To je logické, jelikož potřebujeme obsáhnout těleso vzniklé rotací. Musíme tedy integrovat přes všechny úhly.

V proměnné z je situace také jasná, budeme integrovat od z = 0 do z = v, abychom vyčerpali celou výšku kužele.

Pozor si ovšem musíme dát v proměnné r. Aktuální r (tedy vlastně aktuální vzdálenost od osy z) se totiž podle vztahu (5) mění v závislosti na z – musíme tedy integrovat nejdříve podle r a teprve poté podle z (jinak je pořadí integrace libovolné). V proměnné r budou mezemi r = 0 a r = (v-z)R/v (dle vztahu (5)). Tuto druhou integrační mez označíme pro přehlednost jako r₀.

Nyní sepíšeme výše uvedené poznatky do výsledného integrálu:
\[z_\mathrm{T}\,=\,\frac{3}{{\pi}R^2v}\int_0^{2\pi}{d\varphi}\int_0^v(\int_0^{r_0}{zrdr)dz}\,=\,\frac{3{\cdot}2{\pi}}{{\pi}R^2v}\int_0^v{[\frac{1}{2}zr^2]_0^{r_0}}dz,\] \[z_\mathrm{T}\,=\,\frac{3}{R^2v}\int_0^v{(zr_0^2)}dz\,=\,\frac{3}{R^2v}\int_0^v{z{\cdot}(\frac{R^2(v\,-\,z)^2}{v^2})}dz,\] \[z_\mathrm{T}\,=\,\frac{3}{v^3}\int_0^v{z(v\,-\,z)^2}dz.\]
Tím jsme však integrál převedli na tvar uvedený v původním postupu ve vztahu (6), také integrační meze jsou stejné – alternativní výpočet tedy dává stejný výsledek.
Odpověď
Souřadnice těžiště homogenního přímého kužele v námi zvoleném souřadném systému jsou:
\[x_\mathrm{T}\,=\,0,\] \[y_\mathrm{T}\,=\,0,\] \[z_\mathrm{T}\,=\,\frac{v}{4}.\]